| 評論・随筆・記録 |
| 管弦楽《名曲50選》 1994 | 管弦楽《続・名曲50選》 2004 |
| 西田幾多郎と京都学派 2001 | スティーヴ・ライヒの音楽 2024 |
| フェルマーの最終定理と未解決問題 2003 |
| 高木貞治と類体論 |
| 2025年 執筆 |
| 目次 |
| 貞治は, 上述したような代数や解析の専門書を執筆する一方で, 6冊の啓蒙書あるいは随筆 |
| 高木貞治『數學雜談』共立社, 1935, 全264頁. 高木貞治『過渡期の數學』岩波書店, 1935, 全38頁. 高木貞治『近世數學史談』河出書房, 1942, 全216頁. 高木貞治『數學小景』岩波書店, 1943, 全227頁. 高木貞治『數の槪念』岩波書店, 1949, 全94頁. 高木貞治『數學の自由性』考へ方硏究社, 1949, 全128頁. |
|||
| を執筆している. 『數學雜談』は,『輓近高等數學講座』および『續輓近高等數學講座』に執筆された数編の記事を一冊に纏めたもので, 貞治がちょうど60歳の時の著作である. [百年史下] によれば,『輓近高等數學講座』は, 1928年4月から1929年10月にかけて刊行され,『續輓近高等數學講座』は, 1930年1月から1931年12月にかけて刊行された (pp.133-134). 出版社は何れも共立社である. 既に記した通り, 現在では『近世數學史談』との合本版も存在するが, 以下の引用は |
| 高木貞治『数学雑談2版』共立出版, 1970, 全274頁. | |||
| による. |
 『数学雑談』共立出版, 1970 |
| 啓蒙書とは言え, 貞治の執筆姿勢は極めて真摯である. 冒頭部の文章から抜粋しよう. |
| 雑談\(\!\:\)=\(\!\:\)無駄話という古典的公式がある. (中略) しかしながら筆者は無駄なるべき話を書く意向を有するのではない. 筆者はこの輓近高等数学講座を一つの「ユニヴァーシテー・エキステンション」(大学延長) と認める. (中略) 大学で数学をする場合には「コロキゥム」なるべきものがある筈である.「コロキゥム」を仮に訳して雑談という. |
|||
| 貞治は冒頭部でこのように述べ, 雑談の中から既成でない新たな数学が産まれる可能性を指摘する. 新たな内容でなくとも, しばらく停滞していたものが,
雑談を通じて何かの機縁で一躍表舞台に躍り出る可能性もあるというのである. 目次から内容を拾ってみると, |
| 1. 格子の幾何学 (ピックおよびミンコフスキの格子点定理, クロネッカーの稠密定理など) 2. 平行線の話 (初等幾何における公理の再検討, サッケーリの平行線公理, ポアンカレの擬平面と擬空間) 3. 複素数 (複素数の幾何学および解析学への適用, 代数学の基本定理, 四元数および広延論など) 4. 無理数 (連続の公理, アルキメデスの公理, デデキントの切断, \(\varepsilon\)-\(\delta\,\)論法, 集合論など) 5. 数理が躓く? (ラッセルのパラドックス, カントールの対角線論法, 選択公理など) 6. 自然数論 (ペアノおよびデデキントの自然数論) |
|||
| となっており,『新撰算術』と同様 (あるいはそれ以上に), ここでも貞治が「数の体系」に固執する様子が窺える. これは『數の槪念』で更に深化され, 精密化されることになる. 貞治は, 生涯に亘って「数」の構造を徹底的に追求したのであった. 『新撰算術』と異なり,『数学雑談』には, 読者を一気に惹きつけ最後まで読ませる牽引力がある. それは, 貞治の数学思想および数学史談が随所に示されているからであり, これらも本論に付随する興味深い「雑談」となっているのである. 例えば, 玉突き台を題材としてクロネッカーの稠密定理と天体との関連性 (エルゴード性) を述べたり (pp.28-29), 地上と上空における景観の差異を喩えにして実函数に対する解析函数の経済性を述べたり (p.94), 公理なるものは後から顧みれば明白だが無数の命題から選び抜き公理と銘打つ過程を「冀北の馬群の中から, 千里の馬が見出された」と喩えたり (p.127) する. また, 整列可能定理に纏わる [烏有生] と [青年B君] の対話には, ツェルメロの時代から現在に至るまで続く論争の一端が垣間見える.「万人向きの味付け」を「矛盾を含む要求」とした上で,「100%無味」であるランダウ式の自然数論は, 消化すれば (薬が利いて) 骨まで通る痛味を覚えるが, 味付け無しは「味う勿れ」ではなく「存分に味え」と述べる (pp.243-244). 殊に, 自身の学生時代および著作を回顧するエッセイ (pp.119-122) は, この『数学雑談』において最も惹かれる部分であろう. |
| 1898と1904との間に於いて, 筆者は欧州留学の機会を享受した. 本郷の図書室での独り合点には, 聊か不安がないでもなかったが, 学問の源泉に接触したならば, 源泉の源泉ともいうようなものがあるのではなかろうか, というような空想を抱いていたのである. 1898か1899かにベルリン大学に於ける S.翁の講筵で Weierstrass 直伝の無理数論というものを, 緊張を以って聴いたこと勿論である. その結果は大なる安定感であった. | |||
| 「S.翁」はシュヴァルツ (前出, §2-4) を指す. (後に『回顧と展望』に述べられることになる) シュヴァルツによるヴァイエルシュトラス (前出, §2-1) へ崇拝ぶりは, ここに初出となるのである. |
| 翁は Weierstrass の一言一句を聖典として取り扱う人であったが, 如何に Weierstrass でも, その一言一句が凝固して聖典に化石してしまうのでは, 迅速に時の風化作用を受けずばなるまい.「ケルペル」論に立脚した当時の青年 Dedekind の深みも, 集合論を握っていた青年 Cantor の強みも感得されない. (何トイフ石頭の形式主義デアラウカ!) 青年の心は動き易い. Riemann へ! ゲッチンゲンへ! その頃既に偉才 H.先生の壮年的禿頭が陸離たる光彩を発揮していたのである. コーシー何者ぞ, ワイヤストラス何者ぞ, 批判的数学の最高峰は, 皮肉にもガウスの Disquisitiones と同じように, 世紀の変わり目に現出した「幾何学原理」ではないか. | |||
| 『回顧と展望』には見られない, 青年貞治の意気込みが熱気を帯びて伝わってくる. なお, 上記引用部における括弧内の文言は, 初版の『續 輓近高等數學講座 2.A』(共立社, 1931, p.3) に見られるもので, 上掲の [2版] では削除されている. 「無理数論に筆を執るのは, 今度が三度目」という貞治は, 一度目の『新撰算術』(1898) は学生時代に乱読した洋書を縦書きに「排出」したもので, 二度目の『新式算術講義』(1904) も「熟慮の遑もなく, 拙速に書い」た. これらの著作はそこに起因する「未定稿」であり, その後二十数年間, 書き直す機会がなかったと述べる. 貞治は, ヒルベルトの『幾何学原理』 |
| [Hilbert3] D.Hilbert "Grundlagen der Geometrie" B.G. Teubner, 1899, 全92頁. | |||
| に代表される, 素朴な幾何学的直観によらない無理数論の構築において, 量と数との差別を「克服されたる立脚点」と述べる. しかし,『幾何学原理』が冷遇する連続的な量 (一次元幾何学) を隔離した無理数論は存在理由を欠く. これが, 貞治が『新式算術講義』を執筆した所以であった. |
| 明治37年 (1904) の発行である. やくざな著書の出版年月に拘泥する筆者の偏執を (中略) 弁解する (後略). 思出多き本郷の図書室は1923年の震災に大損害を被って, 遂に取り毀されてしもうた. そこに仮住いの間の「エピソード」であるが, 例の叢書の或る一巻に於いて, Borel が効率的なる解析教程の重要性を高調する序に, Baire の Leçon を推奨しているのを見たのであった. (中略) 繙いて「ギックリ」したのであったが, 早速扉を見て, 1907 とあるので安堵した. しかし緒言の中に「無理数, 極限及び連続性」に関する部分は, 既に1905年に別冊として出してある由が, 記してある. それも1905ならば差支えない. このようなものがあるのに, 1904の新式算術講義が, 1912或は1916では, 著者の立場がなくなる. Baire の Leçon はフランス式の流麗なる「スタイル」で実にみごとに書いてある. Borel が推奨するのも尤もである. あのような立場から無理数論を組立てることは, 筆者も「新式算術講義」で試みたのであった. (中略) Baire の Leçon に於いて望蜀なるは,「具体的量」(Grandeurs concrètes) との連絡が, 解析教程らしく, 投げ遣りに扱われている点である. さて第三回の本稿が再び未定稿的に終るのを筆者は遺憾とするのである. |
|||
| 『新式算術講義』における無理数論が貞治独自の工夫によるものであることがここで告白される.『数学雑談』を「決定稿」にしたかった貞治であるが, しかしこれも「未定稿」に終わる運命にあった. 連続的量は斉質的 (各区間が同型) な連続集合であるが, 斉質性は連続集合の必要十分条件ではない. 順序の公理と-連続の公理のみから一次元的連続量を定めることの困難性に直面した貞治は, 次のように述べる (pp.181-187). |
| 本稿に筆を執るに当って, 泥縄式に心当りを当って見たが, 間に合わないで, 止むなく第三回の未定稿を心ならずも書くような仕末になったのである.
(中略) 今時, 無理数論の未定稿を書くのは筆者の酔狂に過ぎない. 終結はしていても如何に終結しているかを問題にして見ただけである. 第四回の無理数論を書くべき機会が筆者に与えられるや否や, 段々覚束なくなるから,「何がこれを未定稿にしたか」を告白して, 筆をおくのである. (昭和五年二月) |
|||
| ところで, ランダウ (ディリクレ) が指摘したペアノの加法の定義における瑕疵を回避する中で, 貞治自身が得た着想 (帰納法によらない加法の可換則と結合則) が解説される (pp.251-252). この手法は貞治独自の工夫によるものであろう.『数学雑談』の初出となる『續輓近高等數學講座 2.A』(共立社, 1930) とほぼ同じ時期に, これに関する論文が執筆されているからである (前節 [高木25] 参照). |
| 『数学雑談』の出版と同年の出版物に, 昭和9年の11月に大阪帝国大学理学部数学教室にて開催された貞治による講演4回分を纏めた小冊子 |
| 高木貞治『過渡期ノ數學 大阪帝國大學數學講演集』岩波書店, 1935, 全38頁. | |||
| がある. 出版されたのは貞治が60歳の時であったが, 講演はその前年に行われたものである. 当時, 大阪帝大理学部では, 学生を対象とした (数学者による) 講演を年に数回, 企画しており, それを「一般社會ノ數學知識ノ進歩に卑益スル所決シテ少クハナイデアラウ」として出版したのであった. 4回の講演は4日連続で行われ, この小冊子の目次は, 過渡期の数学 (11月5日), 解析概論 (11月6日), 数学基礎論と集合論 (11月7日), \(p\)-進数と無理数論 (11月8日) の4項目から成る. 「講演者の辞」として, 貞治は |
| 講演トハイフモノノ, ソレハ學術的ノ講演トイフヤウナソレデハナクテ, ムシロ座談, 或ハ事實ニ卽シテ言ヘバ, 講義室デノ立チ話シデ, 要スルニ, 不用意, impromptu ナル, イワユル漫談トイツタヤウナモノデアツタノデス. | |||
| と述べている. 自身の講演が筆記され, 況してや出版されようなどとは全く想定していなかったらしい. 実際, 各日における講演内容は, 貞治が日頃から抱いている随想のようなものであり,
数学的には特にこれといった纏まりはない. しかし, ここに示される貞治の数学思想はやはり看過できない重みがある. 「過渡期の数学」では, 貞治は, 数学の発展は一様ではない, 即ち |
| first approximation トシテ Treppen-Funktion ト見ラレル. 卽チ階段的ニナツテヰル (圖.1). 進歩ノ速度ハ階段的ニ昇ツテ行ク. 更ニ詳シク云ヘバ圖.2ノ樣ニナルデアラウ. | |||
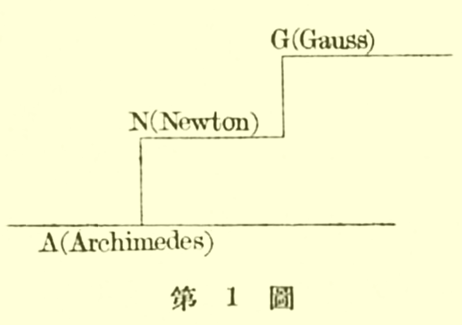 |
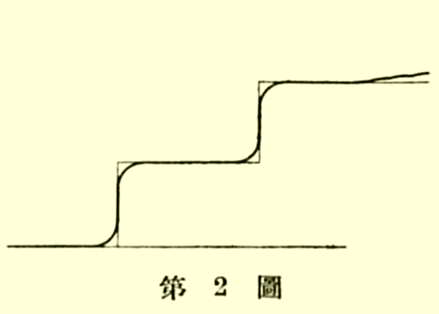 |
| と述べ, 階段の直後に数学者の名が密に集まると指摘する. 数学が発展する様子を貞治は川の流れに喩える. しばらく先へ進むと何らかの障害により横に拡がり, 障害を乗り越える高さに達すると一気に勢いを得て流れ出すというのである. ニュートン (Isaac Newton, 1643-1727) やガウス (前出, §2-2) などの出現は, 数学史の流れに活力を与えたのであった. カントール (Georg Cantor, 1845-1918) は「数学の本質はその自由性にあり」と言った. 真の Freiheit (自由性) がなければ数学において重要な拡張は得られない. 抽象化は拡張の一つであり, 種々の具体的なもの全て含む新たな概念を作ることである. 現代は数学史における過渡期時代 (急激に変化しつつある) と言える. |
| 過渡期の數學ノ特徴ハ第一, 非常ニ急激ニ變ル故少シ懶ケテヰルト分ラナクナル. 興味ノ對象ガ變ツテ來ル. (中略) コレカラ勉強スル者ハ早ク專門ヲキメナイデ深クト云フヨリハ早ク廣ク行ツタ方ガヨイ. 傳統的ノ分類ニヨツテ何ヲヤラウナドト云ハナイ方ガヨイ. | |||
| 貞治自身は, 抽象化を牽引するタイプの数学者ではなかったが, 抽象化の価値を認め, 若い数学者には積極的にこれを学ぶよう奨めていたようである. 彌永昌吉や河田敬義など, 貞治の少し後の時代の数学者達が幅広い数学的教養を身に着けていた背景には, 貞治の少なからぬ影響があったものと思われる. 第2日目の「解析概論」は, 著書『解析概論』に関する言及ではない (この講演時には, この著書はまだ出版されていなかった). 但し, 既に大学においては「微分積分学」の講義を担当していたのであり, 貞治は, 講義の中で得た感慨をここに述べたのであった. 講義で全ての概念や定理を述べる余裕はなく, 内容の取捨選択を要する. 伝統に束縛されることなく, "essential" と "torivial" を見極めた上で,「モツト自由ナ立場デ極ク初等的ナ萬人向キノ解析概論ノ出ルコトヲ希望スル次第デアル.」と結んでいる. 先述したように, 貞治は, 後に『解析概論』を執筆することでこの「希望」を自ら実践したのであった. 第3日目の「数学基礎論と集合論」および第4日目の「\(p\)-進数と無理数論」は,『数学雑談』後半部の内容と重複する. 貞治の疑問はここでも完全に解消されるには至っておらず, その意味ではやはり「未定稿」の感は否めない. |
| 貞治が著した上掲の啓蒙書における白眉は『近世數學史談』であろう. ガウス, コーシー (Augustin Louis Cauchy, 1789-1857) , アーベル, ヤコビ, ガロア, ディリクレなど, 一流の仕事をした数学者の人物像や業績およびその数学史的な位置づけなどが, 興味深く濃密に描かれる. 貞治流の独特な口上は, 読者を最後まで一気に読ましめる力をもつ. 実際, この著書により感化された数学者が多いことも周知の事実であろう. いや, 数学者に限らない. 本稿の冒頭に挙げた哲学者西田幾多郎も, |
| [西田] 西田幾多郎『高木博士の「近世數學史談」』/『西田幾多郎全集 第12巻』岩波書店, 1989, p.235. | |||
| において「大數學者の着眼點とか數學的思想の發展の經路とか云ふものに深い興味を有つた」と述べている. 『近世數學史談』の初出は,『續 輓近高等數學講座 15.A』および『續 輓近高等數學講座 16.C』(共立社, 1931) である. 執筆当時, 貞治は56歳であった. 後にこれは『近世數學史談 輓近高等數學講座 第2卷』(共立社, 1933) として一冊に纏められた. その「序」には, |
| 先きに共立社輓近高等數學講座刊行中社主の要請によつて, 匇卒の間に本編を草した (中略), 意に滿たない所は多いが些少の訂正を加へるに止めた. | |||
| とある. 初出の二分冊には「序」文はなく, 直ちに本文が開始される. 目次の項目を順に列挙すると, 正十七角形のセンセーション, 近世数学の発端, ガウス略歴, 研究と発表, ガウス文書, レムニスケート関数の発見 (\(\sigma\,\)関数, \(\theta\,\)函数), 数学計算とガウス, 書かれなかった楕円関数論, パリ工芸学校, 3つのL., 工芸学校の数学者, コーシー「教程」および「綱要」, 函数論縁起, パリからベルリンへ, アーベル 天才の失敗と成功, ベルリン在留研究生, パリ便リ, アーベル対ヤコビ, 初発の楕円関数論, ガロアの遺言, ディリクレ小伝, 3人の幾何学者, 追記, である. 前掲 (§2-1) した『近世數學史談』第2版 (河出書房, 1942) においては, 上記本文に若干の言い換えや書き加えがあるほか,『回顧と展望』(附録1),『ヒルベルト訪問記』(附録2) が追加されている. その4年後に出版された,『數學雜談』との合本版 (共立出版, 1946) 所収のものは,『近世數學史談 輓近高等數學講座 第2卷』の再販である. 初版の再販であるから,「附録1,2」は掲載されていない. 第2版の「序」には, この著作に対する貞治の気概が記されている. |
| 振へ振へ, 科学! 與れ與れ, 科学! 行進曲は勇壯である. その裡にあつて, はかない舊稿の校正刷を讀みつつ, 思ふ所なきにしもあらずである. ――科學は何に由つて與るか. ガウスやアーベルは, 手を拱いてその出現を待つ外はあるまい. 國難に促されて隆興した巴里工藝學校は他山の石であるが, そこで物を言つたのは人的「資源」のみである. 數學勃興期の史談が英雄傳に終始するのも止むを得ないであらう……. それら英雄の風丯を紹介する小照の挿入は出版所の思ひ付きであるが, 讀者の感興を惹き得るものと信ずる, 旣にガウスが, アーベルの訃音に接して, 肖像が見たいと言つたといふから, 爭はれないものは人情である. そこまでは筆者の史談は行届かない. ゲーテがバイロンの肖像を見たか, 見なかつたか, そこにはエッケルマンの索引でも繰つて見ようといふ手掛かりがある. 年代といひ, 事情といひ, そつくりだから, 興味は一段と高潮する. 楕圓函數發見のローマンスに筆を費やした史談の筆者は, 結局, 椽の下の力持をしたことにもならうか. |
|||
| この第2版を現代の仮名遣いに改めた版が |
| 高木貞治『近世数学史談 3版』共立出版, 1970, 全195頁. | |||
| である. 以下, 引用する際はこの版を (明らかな誤植を修正の上で) 使用することにする. |
 『近世数学史談 3版』(共立出版, 1970) |
| 約200頁に及ぶこの著作のうち, 4分の1以上がガウスの話題であり (pp.1-57), 4分の1弱がアーベルの話題である (pp.95-144). 他の数学者と関連する記述を含めれば, 彼らが登場する頁はさらに増える. 貞治は, この二人を主題とした理由を「彼等の口から当時の数学界を語らしめる為」(p.172) と述べているが, やはり貞治自身が特にこの二人に関心を寄せていたのであろう. ガウスの業績は多方面に亘るが, 貞治にとっては [Gauss D.A.] および [Gauss1] の存在が大きかったし,「五次以上の方程式における代数的解法の不可能性」や「楕円関数」におけるアーベルの功績に対しても心酔していたものと思われる. 『近世数学史談』は, 有名な『ガウス日記』の第1項目の引用から始まる. それは, "Principia quibus innititur sectio circuli ac divisibilitas eiusdem geometrica in septemdecim partes etc. Mart. 30. Brunsvigae."「円の等分に基づく原理, それに由って幾何学的に十七等分等々. [1796年] 3月30日. ブラウンシュワィヒに於て」という, 円分方程式論に纏わる正17角形の作図可能性を示唆するものであった. 『ガウス日記』の原著はラテン語で書かれており, 146項目に亘る研究題目のメモが, 1796年3月30日から1814年7月9日にかけて記載されている. 何れの項目についても, 具体的な計算や証明はほとんど記されず, 簡単な研究内容と, 得られた結果のみが記されている. 私が所蔵する |
| [Gauss 日記] C.F.Gauss "Mathematisches Tagebuch 1796-1814" Verlag Harri Deutsch, 2005, 全234頁. | |||
| には, ラテン語による直筆 (下図参照) および活字の対照表記 (pp.26-63) と, 羅語および独語の対照訳 (pp.66-131) がある. |
 『ガウス日記』第1項目, 自筆 ([Gauss3] p.26) |
|||
| [Gauss 日記] の冒頭に掲載されたビアマン=クルト (Kurt-Reinhard Biermann, 1919-2002) によるガウスの略伝は, ガウスの生涯と業績, 性格や特徴が詳しく解説されている. また, 後半部には, ガウスに関する研究文献 (pp.134-145) に基いて, 146項目の全てに関して個別に解説が施されている (pp.146-233). 19歳のガウスは, \(x^n\!-\!1\!=\!0\:(x\!\not=\!1)\,\)の根を適当に二組に分けることで円周を\(\,p\,\)等分し得ることを看破した.「高等整数論の研究は今もこの後も数学中最上のもので, 如何程美しい天文学上の発見でも高等整数論が与える喜びに比べれば言うに足らない」と述べるガウスは, 一般論を見出した後, \(p\!=\!17\,\)に関する計算を簡潔に示すのであるが, その計算方法の鮮やかさは読者を驚嘆させるものである. 貞治は,「十七角形でガウスが欣喜雀躍したのではあるまい. 伝説を製造する世間が驚いたのであろう.」と言う (p.10). 実際, 上記の手法を弟子のゲルリング (Christian Ludwig Gerling, 1789-1864) に報告するガウスの口調は, 至って冷静沈着である (貞治が引用したゲルリングへの報告も上記 [Gauss 日記] に見られる).「才に恵まれ寿に恵まれた彼は十九世紀の前半を通じて高く時流を超越して実に一世の泰斗であった」(p.12) と, 貞治も畏敬の念をもってガウスの業績を伝えるのである. 『近世数学史談』に述べられるガウスに関する逸話 (pp.13-28) は, 読者を感化せずにはおかないであろう. 数多くの業績を遺したガウスであるが, 順風満帆の生涯ではなかった.「数学の考究に於ては何よりも妨げられざる, 切り刻まれざる時間が必要」と述べるガウスも, ゲッティンゲン大学天文台長兼数学教授としての観測や講義に時間を割かれ,「まとまった大きい理論的の仕事をする暇がな」く,「その苦しさは言語に絶する」と嘆く. 「思想の豊富なるに比して発表する所の甚だ少なかった」ガウスは「研究の成果が完成されたる芸術的作品の如き形式を具え」ぬうちは発表しなかった, とするザルトリウスの評伝 (前掲書 [Sartorius] ) や,「建築が落成した後に足場が残る」ことを忌避し,「主要部の掛けている建築を提出したくないのであって, 決して外観の美を欲するのではない」とする, ガウスの弟子シューマッハー (Heinrich Christian Schumacher, 1780-1850) の宛の書簡を紹介する貞治は, このようなガウスの数学的態度を, 当時の数学界のガウスに対する無理解が原因であろうと述べる. 虚数を用いた証明や非ユークリッド幾何を外に持ち出すことで, 無用な論争や応酬が生じることをガウスは警戒したのである (pp.18-20). |
 C. F. ガウス (1777-1855) |
| 余談であるが, このようなガウスの数学的姿勢を読むたびに, 私は, "Hyperfunction" の創始者, 佐藤幹夫 (1928-2023) を想い出す.「発表する所の少な」い理由はガウスとは異なる. 佐藤の場合は, |
| [木村] 木村達雄編『佐藤幹夫の数学』日本評論社, 2007, pp.44-45, p.53. | |||
| によれば, 超函数の萌芽時代, 新たなアイディアをや手法を話題にしてもほとんど理解されないことに失望し, 英語が苦手であったこともあって論文を書かなくなったというのである. 佐藤の理論は, やがて小松彦三郎 (1935-2022) を中心として徐々に若手研究者に理解されるようになったことは周知の事実である. 研究グループの先鋒である柏原正樹 (1947- ) が今年 (2025年) の3月に\(\,D\,\)加群理論における業績をもって我国初のアーベル賞受賞者となったことも記憶に新しい. 佐藤のような例は特殊であるが, 一流の数学者たち同士の間では, 新しい理論の構築や新定理の発見に関する先発権争いは熾烈を極める. 同一方面の研究を進めてきた学者達の間において僅かでも他者より発表が遅れた場合は, それまでの研究の価値や労苦は無に帰する. 自力で労苦を重ねて得た成果であっても, 既に流布した研究成果と同程度のものならば, 発表する意義を失うからである. とは言え, 充分に検討することなく先を急いで発表した場合, その論理に僅かでも瑕疵が見つかろうものならば, 数学者として致命傷を負うことになる. しかし, ガウスは定理や理論の先発権には頓着しない. 貞治は次のように記している (pp.21-22). |
| 自分では意に満たないから発表しない, いずれその中に暇があったら整理して発表するであろうと, 友人や門弟には告げておく. 他人が発表すれば, それは自分が既に久しき以前, 何年何月に発見していたことだと言う. 知らないものは「うそつき」と思うであろう. (中略) 実際はうそではないのだから, 尚さら憤慨せざるを得ないのである. | |||
| ルジャンドル (前出, §4-8) が最小二乗法に関して公表した際, ガウスは以前から久しくこれを使用していたと言明し, ルジャンドルを怒らせている. ヤコビが発見した楕円関数についての定理をガウスはその20年ほど前に発見していると知らされたルジャンドルは, ヤコビ宛書簡の中で「ガウス氏ともあろうものが, 貴下御発見の諸定理を, 既に1808年以前に知っていたなどと言いふらす」ことに対し「他人の発見を横奪せんとする厚顔は思量の外」と怒りを露わにし,「斯の如き発見, 予の観る所では数学に於て未曽有なる発見に, 逢着したとするならば, 彼は速かにそれを発表しないでいる筈がない」と断じたという (pp.21-22). この遣り取りに対し, 貞治は, |
| ルジャンドルは所謂発表の先発権に拘泥しているが, 世界は広くて人は様々である. ルジャンドルがヤコービから聞いて知った「未曽有」よりも, ずっと広い意味での「未曽有」をガウスは秘蔵していたのである. | |||
| と記す (p.22). 貞治がここに記す限りにおいては, ヤコビやアーベルにはガウスに対する嫉心は見られない. むしろ, ガウスを目標として励んだという.
ガウスに対する猛烈な妬みや嫉みを剥き出しにするのは, 独りルジャンドルのみである. 楕円関数研究に関してアーベルも同等の研究成果を挙げているとヤコビから聞かされたルジャンドルは, 二人を賞賛すると共に「侵入者G氏などは既に久しく前からそれを発見していななどとは言わないが宜しかろう」,「ガウス氏は楕円関数に関して未だ何も発表していない. (中略) 若しも彼が先を越され, 或は又凌駕されたとしても, それは彼がその研究を秘密の雲に包んでおく報いである」と述べる (p.23). 貞治は, これに関して, |
| アーベルの楕円函数論 (Recherches) がクレルレ誌の第2巻に掲載されたとき, クレルレはガウスにも寄稿を乞うたが, ガウスからアーベルの論文を賞讃する返書を得て, 非常に満足して早速アーベルにそれを知らせている (1828年5月18日)「友よ, 喜べ」というのであるが, このような田舎の気分をパリの老大家などは知らなかったのである. | |||
| と記すのである (p.24). 19世紀の西欧における数学史劇の一端が, 貞治の巧妙な筆致によって鮮やかに活き活きと描き出されおり, 読者にとっては大変に痛快である. [Gauss 日記] に加え, ガウスが遺した学術関連書 (貞治の言う「ガウス文書」) は, ガウスが如何に早熟であったを示している.「Leiste 著の算術教科書」には,「初学者らしい練習問題と交錯して, 当時の数学界では思いも寄らないような独創的の研究」―― 例えば「楕円関数」が記されているという (p.26). ここに現れる「算術教科書」とは, 1790年に出版された, ライステ (Christian Leiste, 1738-1815) の『教育のための算術と代数』 |
| [Leiste] C.Leiste "Die Arithmetik und Algebra zum Gebrauch bey dem Unterrichte" Wolfenbüttel, 1790, 全114頁. | |||
| を指すのであろう. 四則演算から始まり, 冪根計算や代数計算, 不定方程式や高次方程式, 無限級数や連分数などが解説される小冊子である. ガウスの早熟ぶりを貞治は次のように伝える (p.27). |
| ガウス文書を見て驚かれることは, 彼が遠く時世に先行して独自の世界に往したことである. 我々は今更ながらガウスの偉大なる天才を感嘆するのである. 十九世紀数学の最初の飛躍は楕円函数の発見である. 然るにガウスはアーベル, ヤコービに先だつこと三十年にして既に楕円函数を発見している, 少なくとも発見の端緒を確実に把握している. 又デデキンドに先だつこと五十年にして既に modular 函数を発見してアーベル, ヤコービを凌駕しているのである. しかもそれは一例に過ぎない. |
|||
| ゲッティンゲン時代の関係諸氏との往復書簡に関して, 貞治は「当時の数学の活きた歴史の映画ともいうべきもの」と表現しているが, 貞治自身による史談もこれに優るとも劣らないであろう. 中学および高校時代の私は,『レ・ミゼラブル』,『モンテ・クリスト伯』,『アンナ・カレーニナ』などの文学作品に憑りつかれ, 残りの頁が減少していくことを惜しみながらこれらを読み進めた.『近世数学史談』も (これらの名作古典文学とは質は異なるものの) 読了が惜しまれるような著作であることは間違いない. 本節は, 貞治の著書の紹介や書評を目的とするものではなく, そこに見られる貞治自身の数学思想を紹介することであった. とは言え,『近世数学史談』に限って言えば, ある程度の内容を示さなければ貞治の言明は具体性に欠けた空言に陥る可能性がある. 敢えて著作内容を併記する所以である. 貞治は,「ガウス文書」について, ガウスの「完成されたる芸術」の成立過程, すなわち「建築が落成した後に」ガウスが隠そうとした「足場」を暴露するものであると述べ,「アトリエに闖入して自由に下画を掻き廻わすことができる」と述べる (p.28). これに基いて, 以下, レムニスケートの発見に至る経過が詳細に示されるのである. |
|
[Gauss 日記] を見ると, 第32項目 (1796年9月9日付) に初めて楕円関数の逆関数が現れ, 翌日 (第33項目) には超楕円積分の逆関数が現れる.
レムニスケート\(\,\rho^2\!=\!2a^2\cos2\theta\,\)の弧長\(\,\displaystyle{\int_0^{\rho}\!\!\frac{2a^2\,d\rho}{\!\!\sqrt{\!\:4a^4\!-\!\rho^4\!\:}}}\,\)から\(\,\displaystyle{\int\!\frac{dx}{\!\!\sqrt{\!\:1\!-\!x^4\!\:}}}\,\)を得たのが1797年1月8日
(第52項目) であった. |
|
同年3月19日 (第60項目) にはレムニスケートの\(\,n\,\)等分から\(\,n^2\,\)次方程式が生ずる旨が記され, 3月21日
(第62項目) にはレムニスケートの周を5等分しうる旨が記される. \(n\!=\!5\,\)の場合, 25次方程式の中の (5個の実根を除く)
20個の虚根の意義を求めてガウスは複素函数の考察へと向かったという. この経緯を, 貞治は「函数論の芽生」と記す (p.32). 貞治は, ガウスに関して, 複素数を用いた\(\,s(n),c(n)\,\)の計算, 無限級数や無限積の取り扱いの習熟性, \(\,\log4.81048\!=\!\displaystyle{\frac{\!\:\pi\!\:}{2}}\,\)なる推測 ([Gauss 日記] 3月29日, 第63項目), テータ関数の級数表示, \(e^{-\pi}\,\)および\(\,\displaystyle{e^{-\frac{\pi}{4}}}\,\)の近似値計算など,「ガウスが数字的計算に驚くべき才能を有したこと」を示す種々の逸話を紹介する (pp.29-49). |
| ガウスが如何にしてこれらの結果に到達したかは例の通り明らかでない. (中略) 既成の数学を学修するものは, その容易なる道を歩む (中略). 「幾何学に帝王道路なし」という諺もあるが, 既成数学は実は帝王道路である. 帝王道路の開拓は天才の創意の恩恵であるが, その創意は何処から来るか, それは創意者自身も知らないであろう. 全く天啓である.(中略) しかしそれは僥倖ではあるまい. (中略) 非常なる天才が, 更に非常なる勤勉と結び付いていたのである. |
|||
| ガウスの数学的発見が単なる「僥倖では」ないことは無論である. しかし, その驚嘆すべき数多の業績に鑑みる時, ガウスの「天啓」はやはり豊富なる「幸運」に肖るものと思わずにはいられない. 「算術幾何平均\(\,\mathrm{ag}\!\:\mathrm{M}\!\:(1,\!\sqrt{2\!\:}\!\:)\,\)とレムニスケート関数の周期\(\,\overline{\omega}\,\)との関連性」の発見 ([Gauss 日記] 1799年5月30日, 第98項目) や,「超幾何級数\(\,\mathrm{F}\!\:(\alpha,\beta,\gamma,x)\,\)と\(\,\mathrm{ag}\!\:\mathrm{M}\,\)とモジュラー関数との関係」などの発見もその一例と言えよう. 前者を考察する中で, 楕円モジュラー関数\(\,j\!\:(\tau)\,\)を創出する契機となる求和関数 "summatorische Funktionen" |
| \[\displaystyle{\mathrm{F}\!\:(x)\!=\!\prod_{n\!\:=1}^{\infty}(1\!-\!x^n)}\] |
| が登場する (p.55). これは, ガウスの論文『或る特種の級数の総和』 |
| [Gauss2] C.F.Gauss "Summatio quarumdam serierum singularium" Dieterich, 1808, 全40頁. | |||
| において用いられた有理式 |
| \[\displaystyle{\mathrm{T}\!\:(x)=\!1\!+\!\frac{a^n\!-\!1}{a\!-\!1}t\!+\! \frac{\!\:(a^n\!-\!1)(a^n\!-\!a)\!\:}{(a\!-\!1)(a^2\!-\!1)}t^2\!+\!\cdots\!+\! \frac{\!\:(a^n\!-\!1)(a^n\!-\!a)\cdots(a^n\!-\!a^{n-1})\!\:}{(a\!-\!1)(a^2\!-\!1)\cdots (a^n\!-\!1)}t^n}\] |
| であり, ガウスはこれを駆使して「遠くアーベル及びヤコービを凌駕」する\(\,j\!\:(\tau)\,\)の基本領域に到り, のみならず\(\,\mathrm{F}\!\:(\alpha,\beta,\gamma,x)\,\)との関係性を含めた理論を構築しようとしたのであった
(pp.50-57). 貞治は, ガウスの研究過程を顧みて次のように述べる (p.57). |
| ガウスが進んだ道は即ち数学の進む道である. その道は帰納的である. 特殊から一般へ! それが標語である. (中略) 数学が演繹的であるというが, それは既成数学の修業にのみ通用する (中略) 我々は空虚なる一般論に捉われないで, 帰納の一途に精進すべきではあるまいか. |
|||
| ガウスは77歳で長逝するまでに夥しくも輝かしい業績を遺した. 何れの分野においても, ガウスの手法は本質を突いていた. 理論構築に際し, 他の数学者のように別経路を辿ることなく, 常に最善の路をひたすら邁進した. これは結果論であり, ガウスが最初から意図することは難しいと思われる. やはりガウスは「僥倖」に恵まれていたのである. 先述した通り, 整数論の分野では, ルジャンドルの "Essai" (1798) と [Gauss D.A.] (1801) の対比がある. 貞治は「それらが同時代の著作であることは殆んど想像されない」,「ルジャンドルの整数論は史料としてのみ意味を有するが, ガウスの整数論を我々は百年後に至って漸く消化し終らんとしつつある」と述べ,「そこに数学史上の不連続点の最も著しい実例が提供されている」と述べる. 初等幾何学を講義しつつ平行線公理の証明の必要に迫られたルジャンドルは, 行き詰まりを感じつつ袋小路に嵌り込んでいることを認識できなかったのであるが, 一方のガウスは (先述した理由で公表は控えてはいたが) 非ユークリッド幾何に想いを巡らせた. 後年のボヤイ (Bolyai János, 1802-1860) およびロバチェフスキー (Nikolai Ivanovich Lobachevsky, 1792-1856) による非ユークリッド幾何は, ガウスが既に研究済であった事実が知れるに及んで, ようやく学界から承認されるようになったという経緯をもつ. ルジャンドルはここでもガウスに大きく水をあけられたのであった. 楕円積分に心血を注いだルジャンドルについて, 貞治は「どこまでも不運なる老大家は, 竟に逆函数としての楕円函数を拾うことを得なかった」と述べる. 一方,「幸運なる青年ガウスは, 偶然にも始めから逆函数を問題にしていたが為に, (中略) 決して行き詰らない途を歩いていた」のである. その他, \(\varGamma\,\)函数, (先述した) 最小二乗法, 測地学における非ユークリッド幾何学の実験的証明, 曲面論など, 全てにおいてガウスは大先輩のルジャンドルを遥かに凌駕した実績を示したのであった. これらの逸話を並べた後, 貞治は |
| このような対照に於て, 我々は成心を以って L.を抑えて G.を揚げるのではない. 気紛れな「歴史」が稀に見せてくれる面白い芝居が, ここに演ぜられたのである. 新しい時代は新しい人物に由って興るが, ルジャンドルは恰かも過ぎ行く時代を代表するような位置にいて, 新旧分岐の場面を鮮やかにする役をしたのである. | |||
| と記す (p.66). このくだりは, 読者の心に, ガウスに対する賞讃の念とルジャンドルに対する憐憫の情を抱かせるであろう. とは言え, 上記の逸話は数学史上の事実である. 貞治の文体には (咄家の演じる古典落語のように) 読者を惹きつけてやまない魅力がある. これこそが,『わたしの好きな数学史』(後述する『数学の自由性』に収録されている) において貞治が言うところの「面白い史論」に相当するものなのであろう. ガウスに関する逸話は『近世数学史談』の全編に亘って随所に挿入される. 貞治は, ひと通りガウスの業績や人物に関して記した後, 19世紀のフランス数学界に目を向ける.「三つのL」即ちラグランジュ (Joseph-Louis Lagrange, 1736-1813), ラプラス (Pierre-Simon de Laplace, 1749-1827), ルジャンドル (前出) を初め, モンジュ (Gaspard Monge, 1746-1818), ポンスレー (Jean-Victor Poncelet, 1788-1867), フーリエ (Joseph Fourier, 1768-1830), ポアソン (Siméon Denis Poisson, 1781-1840) などに関して言及し, その中で「最も重要なる一人」としてコーシー (前出, §5-3) の名を挙げる. 貞治は「ドイツ人がガウスを看板に出すような所で, フランス人はコーシーをかつぐ. 彼は「フランスのガウス」である.」と述べる (p.79). |
| 彼の思想は断えず揮発せねばならなかった. コーシー全集の巻々を繙く者は精粗錯綜, 玉石混淆に驚かざるを得ないであろう. ここにも「ガウス式洗練! そんな暇は持ち合わせない」人があった. 発表に関して消極的なるガウスと積極を極めたコーシーとは興味ある対照である. | |||
| 貞治による評伝には明記されてはいないが, コーシーが発表に「積極を極め」た理由は先発権争いにあったように思われる. フェルマーの最終定理に関するラメ (Gabriel Lamé, 1795-1870) の手法の横取りと不毛な「似非証明」の応酬は有名であろう. アーベルの才能を見抜けずに彼の功績を無に帰した (p.134) のも, 他者よりもまず自身の功績を優先させるコーシーの自己顕示欲の強さの現れと言えよう. 上記の「ガウス式洗練!」の直前にある「ここにも」とは, p.53 脚注において,「気の早い青年アーベル, ヤコービとは大分違う.「ガウス流の厳格主義!そんな暇があるものか」とヤコービは言うたとやら」を受けての記述であろう. ここで, アーベルに対する「気の早い青年」なる形容は, 読者に誤解を招く可能性がある. コーシーらを中心とする学界から無視されている間に, 自分の得た結論に近い成果を, ヤコビなる若手数学者が発表するのを目の当たりにしたアーベルである (pp.129-131). 貞治は, 他の箇所でアーベルを弁護する (p.132). |
| 当時のアーベルの身になって見るがよい. 彼はガウスのように泰然として先発権などを超越していることの出来る位地に居るのではない. アーベルは「自分ながら驚くばかり多くの発見」をしたけれども,
広い世界にそれを認め得る何人があったか. 旧師ハンステンも親友ホルンボーもアーベルを信じてはいたろう. しかし (中略) 得意らしい高等函数でもパリ学士院に黙殺されているではないか. 楕円函数論はアーベルの最後の切札である. それが思いも寄らない飛入りのヤコービなどに掻き廻されてしもうては, 立つ瀬がないではなかろうか. 借金と肺病とに対抗しつつ, 言葉通り心血を以って書かねばならなかった「楕円積分変形論」である. |
|||
| アーベルには時間がなかったのである. 一般五次方程式の代数的解法の不可能性, (コーシーに放置された) 楕円関数に関するアーベルの加法定理, 楕円積分の逆関数における二重周期性など, 認知されれば一挙に注目を浴びるはずの豊富な数学思想を所持しながらも, その論文の価値を見抜いてもらえなかったアーベルは, 無念のうちに26歳の若さで婚約者に看取られながら結核で世を去ったのであった. なお, アーベルの生涯については, |
| [Stubhaug] ストゥーブハウグ / 願化孝志『アーベルとその時代』シュプリンガー・フェアラーク東京, 2003, 全617頁. | |||
| が最も詳しい. アーベルの死後に彼の元に届いたクレレ (August Leopold Crelle, 1780-1855) の書簡は, 読者を感涙に誘うであろう. 「ヤコービなどに掻き廻されて」なる表現も誤解を招きかねない.「コーシーの紙屑籠に入りそこねた」(p.150) アーベルの論文をヤコビは知る由もなかったのであるから, ヤコビ自身には何の責任もない. 彼も立派な「楕円関数論の創始者」である. 「精力絶倫なる活動家」なるヤコビは, 後に発表されたアーベルの論文『楕円函数の変形に関する一般的の問題の解決』 |
| [Abel1] N.H.Abel "Solution d'un problème général concernant la transformation des fonctions elliptiques" Astronomische Nachrichten, Nr.138, 1828, pp.365-387. | |||
| に接して,「我の及ばざる所, 賞讃するに辞なし」として「感激を極め」た (p.133). 貞治も「ケーニヒスベルヒにいる敵手も立派な男であった.」とヤコビを認めている.
ガウスもアーベルの楕円関数論に関しては賞讃したようである (p.51, p.134). その概要を貞治はガウスのレムニスケート関数論と対照させながら紹介する (pp.137-143). |
| アーベルの論文を読むものは先ずその平明暢達で, 少しも巧を求めずして自然に妙なるを愛するであろう. 恰も彼の書簡の天真流露, 親しむべきと一般である (p.137). | |||
| アーベルは |
| \[\displaystyle{\alpha=\!\int_0^x\!\!\frac{dx}{\!\!\sqrt{\!\:(\!\:1\!-\!c^2x^2) (\!\:1\!+\!e^2x^2)}\!\:}}\:(c,e\!\in\!\mathbb{R})\] |
|||
| として楕円関数\(\,x\!=\!\varphi\!\:(\alpha)\,\)の考察を始め, \(x\,\)を\(\,xi\), \(\alpha\,\)を\(\,\beta
i\,\)としてレムニスケートの弧長と楕円積分を結び付けて加法定理を定めた. 途中, レムニスケートの\(\,n\,\)等分から生ずる「一般等分方程式」が
(\(n\,\)が奇数の場合は) 代数的解法で解き得ることを示し (副産物として得られたアーベル方程式の萌芽), そこから虚数乗法に着眼して乗法公式およびテータ\(\,(\vartheta)\,\)関数の商としての\(\,\varphi\!\:(\alpha)\,\)を得たのであった
(pp.137-142). 貞治は,「アーベルの長所は任意の代数函数の積分に関する所謂アーベル定理の高い立脚点」なるクライン (前出, §1-4) の評に対し,「このような持ち寄りで楕円函数論を合名的に組織するのでは, アーベルの寄与が不当に過大である」とし, 次のように述べる (p.144). |
| ヤコービの\(\,\vartheta\,\)函数, ガウスの modular function と併せて三幅対を作ろうならば, アーベルの虚数乗法が最も適当であろうと我々は思う
(中略) 虚数乗法はレムニスケートの場合にガウスが既にやっているが, \(\vartheta\,\)函数を断えず整数論の問題に応用してガウスを凌がんと力めたヤコービは何と言うだろうか. 彼は他の機会に言うている: 『フーリエ氏などは数学の目的は社会的利益及び自然現象の説明にあると言うが, 氏の如き哲人はすべからく学問の唯一の目標は人間の精神力の発揚 (l'honneur de l'esprit humain) にあることを知るべきである. この見地に於ては, 数の問題も宇宙系統の問題も同等の価値を有するのである』(1830年). |
|||
| ここに引用されたヤコビの言明は,『ヤコビ全集』第1巻 |
| [Jacobi 全集] "C.G.J.Jacobi's Gesammelte Werke Erster Band" G. Reimer, 1881, 全546頁. | |||
| におけるヤコビとルジャンドルの間に交わされた23通の往復書簡 (pp.385-461) の中の, 1830年7月2日付のヤコビの書簡に現れる
(pp.454-455). 時期としては, アーベルやフーリエ (前出) が死去した直後である. この書簡の該当箇所の直前には,「熱伝導を優先的に扱わないアーベルとヤコビを非難していた」とするフーリエの言葉を, ヤコビの業績に関する報告書の中に含めたポアソンに対する苦言が記されている. そこへ上記引用部の言葉が現れ, 直後には, フーリエが自身の研究を完成させずに死去したことに対する遺憾の意が表明されている. 貞治がこのヤコビの言葉をここへ持ち込んだ意図は何であろうか. |
| [志村] 志村五郎『数学をいかに使うか』筑摩書房 (ちくま学芸文庫), 2010, p.212. | |||
| によれば, フーリエは, アーベルとヤコビが熱伝導に有用なフーリエ級数ではなく, (それとは無関係な) 楕円関数論の研究を優先させていることを残念に思っていたという.
ポアソンフーリエやポアソンが, ポアソンの結果とヤコビの仕事との関連性を見抜いていれば, 逆にヤコビがポアソンのテクニックを知り得ていたら云々……, とある. 恐らく, 志村は\(\,\vartheta\,\)関数の変換公式とポアソンの和公式の関係を示唆しているのであろう. 上記に引用したヤコビの見解および志村の私見は理解できる. その上でもやはり, 貞治が「ヤコービは何と言うだろうか」としてヤコビの書簡を引用した意図は判然としないのである. アーベルは, その短い生涯全般に亘って, 貧困と結核に加え, 学界から誤解や黙殺を受けるという不運に見舞われた (ガウスと対照的である). 彼が中学生時代に書いた「五次方程式の解法の発見」は若気の至りとしても,『振子の運動に対する月の影響について』即ち, 後に |
| [Abel2] N.H.Abel "Om Maanens Indflydelse paa Pendelens Bevægelse" Magazin for Naturvidenskaberne" Bd I, 1824, pp.219-226, Berigtelse Bd. II, pp.143-144. | |||
| として発表された論文がシューマッハー (前出) により拒否された (致命的な認識不足を指摘された) のは, ガウスへの門戸を大幅に狭める要因となった
(pp.103-104). その上,『五次の一般的なる方程式を解くことの不可能の証明』は,「証明は略々完全」ながらも「貧乏成る彼は印刷代を節約する為に, 成るべく論文を短縮する必要に迫られて, 説明を十分にする余裕を有しなかった.」 さらに, 標題がいけなかった. アーベルは「代数的」解法の不可能性を意図していた (論文の内容は正にその通りのものである) が, ガウスには「代数的」が抜け落ちて伝わったという (p.108). であるならば, ガウスが論文に目を通したどうかも疑わしい. 後にクレルレ (前出『クレレ誌』) の雑誌発行が始まり, そこに掲載された改訂後のこの論文 |
| [Abel3] N.H.Abel "Beweis der Unmöglichkeit algebraische Gleichungen von höheren Graden als dem vierten allgemein aufzulösen" Journal für die reine und angewandte Mathematik, Bd. 1, 1826, pp.65-84. | |||
| には, ガウスも理解を示したようである (p.108, p.111). アーベルの絶筆となった論文は,『或種の超越函数の一般的性質の証明』即ち |
| [Abel4] N.H.Abel "Démonstration d’une propriété générale d’une certaine classe de fonctions transcendentes" Journal für die reine und angewandte Mathematik, Bd. 4, 1829, pp.200-201. | |||
| であった. 所謂「アーベルの加法定理」である. アーベルが結核で逝去したのはそれから間もなくであった. |
| ドイツに於てクレルレの運動がフンボルトを動かして, ベルリン招聘の議が将に決せんとしたとき, 1829年4月6日アーベルは溘然として逝いた. | |||
| アーベルのベルリン招聘が適ったことをクレルレが如何に喜んだかは想像に難くない. クレルレは直ちにそのことをアーベルに書き送った. しかし, その通知が届いたときには, アーベルは既にこの世の人ではなかったのである (前掲書『アーベルとその時代』参照). ガロアもアーベルと同様, 不運に見舞われて短い生涯を終えた. パリ工芸学校の入試に二度失敗し (p.63, p.146), 入学した師範大学では大学側との悶着の後に放校となった. 過激な政治活動が原因で複数回投獄され, 申し込まれた決闘に負けて21歳で死去したのであった. 翌日に決闘を控えた死の前日, 友人シュヴァリエ (Guillaume-Auguste Chevalier, 1809-1868) 宛に, 方程式が代数的解法をもつ条件 (ガロア理論) および一般アーベル積分に関する新たな定理を書き記した. 同時に「定理の正否ではなく, その重要性をヤコビやガウスに訴えてほしい」とシュヴァリエに訴えたのである (pp.145-147). この「遺書」はガロアの死後すぐに発表されたが,「世上の注意を惹かな」かった. ガロアの方程式論は, 嘗て「ポアソンが異議を挟んだ」が, リューヴィル (Joseph Liouville, 1809-1882) によりガロアの死後14年経ってから公表され, 積分論に至ってはガロアの死後25年経ってからリーマン (Bernhard Riemann, 1826-1866) に発見され, 発表されたのであった. アーベルとガロアを対照させて, 貞治は次のように述べる. |
| ポアソンに抑えられたガロアの方程式論, 叉危くコーシーの紙屑籠に入りそこねたアーベルのパリ論文の運命は奇妙というものであろう. アーベルもガロアも学士院の尻の重さの下に苦悶した. 内気なアーベルは隠忍したが, 高慢なガロアは咆哮した. そこで近世数学史上のローマンスが生じた. アーベルもガロアも処世に失敗したのである. 時代を超越するにも程合いがあって, 二十年, 三十年の超越は危険である. 学士院の尻重きにあらず, アーベル, ガロアの足が軽過ぎたのだ. よい手本に, かのゲッチンゲンの爺さんがある. 賢明というか独善というか, 先生てんで世間を相手にしない. 求むる所のない彼には弱味がない. むしろ求められる位地の強味を (中略) 自家の都合に利用した (後略). |
|||
| 結局,『近世数学史談』は, 独りガウスのみが群を抜いた栄光に浴したかたちに描かれることとなった. 他に, コーシー, ディリクレなどの評伝も興味深く記されているが, 既にこの著作からの引用も大分長くなったから, 最後に巻末の附録2「ヒルベルト訪問記」に簡単にふれるに留めて次へ進むことにしよう. 1932年10月8日の日付をもつ「ヒルベルト訪問記」は, [追想高木] によれば, 岩波講座「数学」に「書信 (チューリヒ・コングレスの状況, ヒルベルト訪問記」(1932年11月) として発表されたという (p.291). 第9回国際数学者会議のためにチューリッヒに赴いた貞治が, 帰り際に立ち寄ったゲッティンゲンのヒルベルトについて記した書簡体エッセイである. この第9回のコングレスについて, [百年史下] には |
| 世界41ヵ国から約700名の数学者が集まった. 日本からは高木貞治が学術研究会議の代表となり, 他に当時ヨーロッパ留学中の若い三村征雄, 南雲道夫,
弥永昌吉, 守屋美賀雄たちが参加した. 高木は類体論の業績によってすでに著名であり, 11名の副会長の1人として選ばれ, また全体講演の座長の1人に推された.
(中略) 閉会式のときに, 大会委員長よりフィールズ賞の提案があり, 4年ごとの国際数学者会議で2人の数学者にメダルを与えることを決議した. (中略) 第1回のフィールズ賞は次回の会議のときから与えられることになり, その選考委員として, バーコフ (アメリカ), カラテオドリ (ドイツ), カルタン (フランス), セヴェリ (イタリア)(委員長), 高木 (日本) が選ばれた. この会議では会長フェターが開会式演説で特に日本からの遠来の賓客として高木を紹介し, 暖かく迎えた. |
|||
| と記されている (p.56). 余談であるが, 矢野健太郎『第11回国際数学者会議〔1950年〕』(『自然』第6巻第1号, 中央公論社, 1951) に記載された第9回 (Zürich) の参会者の数は, 35ヵ国667人, 同行の家族も入れると853人である. ここに現れたフェターこそ, ストラスブール (1920年) での高木の講演で何の反応も示さなかったと先述した (§3-4) 人物その人である. チューリッヒでの貞治は, 目の前のフェターと12年前のストラスブールでのフェターとの応対差に苦笑させられたことであろう. ここで貞治が出会ったのは, 嘗てのように世界数学界の先陣を切って突き進むヒルベルトではなかった. 難治の重病に冒され弟子達の冷ややかな批判を受けつつも独り寂しく数学基礎論に取り組む, 老いた姿のヒルベルトであった. 「ヒルベルト訪問記」において, 貞治は憐みをもって (しかし畏敬の念を失わずに) 次のように述べる (p.193). |
| 数学基礎論は完成してもよい, 叉は完成しなくてもよい. 只H先生は余生を安楽に送られることを望む (中略) 毎日三十匁の生肝を食って不治の難病と戦いつつも, 駿馬も老いては揚足を若い助手連に時々は取られながらも, どうして排中律の証明等等を書かずには居られないでしょう. 余生を楽しむなどとは論外で, 生きながらの餓鬼道ではありませんか. |
|||
| 最後にヒルベルトに関する微笑ましい逸話が三つほど添えられて『近世数学史談』は終る. 以下, その概略のみを記す. (その1) 自宅への来客を迎える直前に, ネクタイを取り替えるよう夫人に促されて二階の自室へ上がったヒルベルト. 客が来訪しても降りて来ないので女中を遣いにやると, ベッドの上で安眠していた由. (その2) ヒルベルトが穴あきズボンを毎日穿いているのに気づいた学生たち. 角が立たぬよう先生に知らせる方法を思案した. ある日, 散歩に出た際, ヒルベルトがトラックの車輪に触れたのを見た一人の学生が, ここぞとばかり「おや, 先生のズボンが痛みましたよ」と伝えると,「ああこれか, この穴は前学期からあいていたようだよ.」 (その3) 自宅に来客を迎えた時の話. 客たちと挨拶や天候の話をして数分が経過した頃, 夫人に向かって「大分お手間を取らせたようだから, もうお暇しようじゃないか.」 以上は概略に過ぎないが, 実際に『近世数学史談』に著されたこれらの逸話に関する貞治の筆致は卓抜である. 貞治による表現は (数学書と同様) 的確で過不足がない上, ヒルベルトの人柄が如実に伝わってくるものである. なお, この書簡体のエッセイの冒頭には「S-君」なる宛名が記載されている. 架空の人物ならば, その人物を詮索することは無意味であるが, 実在するならば, 貞治に近い数学者の中の一人であろう. 「S-君」の可能性として, 苗字で該当するのは, 坂井英太郎, 末綱恕一, 正田建次郎, 菅原正夫などであり, 名前で該当するのは, 中川銓吉, 掛谷宗一, 黒田成勝, 彌永昌吉などである. 後年, 同僚として貞治と親しい関係にあったのは掛谷であるが, 1932年の時点での掛谷は東京文理科大の教授であった. 出版されている対談や談話の記録, 例えば |
| [高木吉江]『高木・吉江兩博士を圍む會』/ 考へ方研究社『高數研究』第3卷第7號 (1939年4月), pp.36-45. | |||
| を見る限り, 貞治が「君」づけで呼ぶのは苗字に対してであり, 直に名前で呼ぶのを見掛けたことはないから, この際, 掛谷 (および中川, 黒田, 弥永) は除外してよいであろう. 坂井は貞治より年齢が上であるから, 貞治が「君」づけで呼ぶ可能性は低い (§2-4 に記したように, 年上の長岡半太郎に対して貞治は「さん」づけで呼んでいる). 一方, 弟子として貞治に近い位置にいたのは末綱であり, 正田および菅原はまだ学位を得るか得ないかの状態であり, 教授または助教授として大学に所属する者ではなかった. 1932年当時, 末綱は, 前年にドイツ留学 (ゲッティンゲン) から帰国したばかりの東京帝大助教授であったから,「S-君」に該当する可能性は高いが, 確証はない. |
| 『近世数学史談』第2版が出版された2年後, 68歳の貞治は, 数学遊戯に関する小著 |
| 高木貞治『數學小景』岩波書店, 1943, 全227頁. | |||
| を上梓した. これは, |
| ・ケーニヒスベルグの橋渡り (一筆書きの可否判定, 迷路脱出法, オイラーの多面体定理など) ・ハミルトンの世界周遊戯 (正十二面体の頂点巡礼, 正十二面体の構成条件など) ・隣組, 地図の塗り分け (四色問題, 平面の塗り分け, 球面およびトーラスの塗り分けなど) ・十五の駒遊び (解法手順の存在問題, 順列と置換) ・魔方陣 (自然方陣の解法, 五進法と五方陣 (超魔方陣)) ・士官36人の問題 (\(n\,\)次オイラー方陣の問題, \(4n\,\)次および奇数次の解法, 半偶数次の検討) |
|||
| を題材として, 初学者でも興味をもって考察し得るように書かれた逸品である. このような専門書以外の啓蒙であっても, 読者を惹きつける話題と話術を縦横に展開する貞治の手腕は見事である言えよう. |
 『数学小景』改版 (岩波書店, 1981) |
| 1943年の [初版] が出た一年後に [再版] が出ている. 誤植や缺落など些細な点はともかく, 貞治にしては珍しく, 数学的な誤謬が含まれていたためである. 1981年に出版された [改版] では, (内容はそのままで) 仮名遣いおよび誤記誤植が改められた. その際, 高木佐知夫 (貞治の三男) による「改版にあたって」なる解題が付加されている. [再販] 出版時における未解決問題で1981年時には解決されていたものもあったが, 内容の改訂は行われていない. 2002年に出版された [現代文庫版] も, (漢数字を算用数字に, 漢字を平仮名に, などの微細な改訂はあるが) [改版] と同一の内容である. 但し,「改版にあたって」は削除されている. 貞治による「序」を見ると, |
| 数学において本質的なるものは, 数学的なる物の見よう, 考え方である. 本書において, 最も簡単なる数個の問題を拉し来って, それらを平易に解決する裡において, 数学的考察法の一斑を説明することが, 著者の意図であった (中略). ただし, 遊戯といえども, 真剣でなくては, 味が出ないであろう. 遊戯は仮託で, (中略) 問題の取扱いに重点が置かれるのである. |
|||
| とある ([改版], pp.vii-viii). この著作で扱われる題材は, 親しみ易いが, 緩やかに思考を巡らさねば理解ができず, 咀嚼吸収しかねるものである.「真剣でなくては,
味が出ない」,「問題の取扱いに重点が置かれる」とは, 取りも直さず貞治自身の数学的姿勢を表現するものであろう. 続けて貞治は記す. |
| 数学には, 雄大な構想もあるが, その雄大は粗大ではない. 極微の抹消においても, 寸毫の齟齬を容さない. 放胆にして, 同時に細心なる所に, 数学の特色があるのだが, いま, 本書で述べる所は, 数学の細心なる方面にある. 題して数学小景という所以である. | |||
| 数学徒以外の一般読者に対しても, 数学に向かう姿勢の最重要点を示す貞治は常に「真剣」である. 遊戯ないし身近な題材をもって読者を惹きつけておき, いざ考察が始まると本格的な数学的姿勢をもって読者を牽引するのである. 初版における貞治の誤謬は, 半偶数次オイラー方陣の問題にあった. 発案したオイラー自身も「多年苦心考究の後, それは恐らく不可能であろうと思われるが, その不可能の証明がむつかしくて, できな」かった ([改版] p.162) という難問である. |
| 6次オイレル方陣の不可能なることは, G.Tarry が試行によって検証したと言われている. その詳細なる報告は, フランス科学協会記事,
1900年号 (中略) に掲載されている由であるが, この文献に予はいまだ属目していない. P. Wernicke (ドイツ数学協会年報, 1910年) は, 一般半偶数次オイレル方陣の不可能性の証明を発表したが, それが誤謬であることが, 近頃指摘された. |
|||
| 最後の「近頃」とは, [再販] (1944) が出版された直前であろうか. あるいは, それ以前に指摘されていたことを貞治が知らなかっただけかも知れない. 貞治は, [再販] が出る直前に, |
| 高木貞治『オイレル方陣について』/ 岩波書店『科学』第14巻第2号 (1944年2月), pp.42-44. | |||
| において, 誤った証明を『数学小景』に載せたことを読者に詫びている. ところが, 転んでも唯では起きないのが貞治である. この『オイレル方陣について』の後半部では, Wernicke の着想を活かし, ラテン方陣の置換群から得られる群作用によってオイラー方陣の構造を再考したのであった. ところで, 貞治による [初版] の誤謬について, 彌永昌吉は |
| 高木先生は初版を書かれたとき, ウェルニッケの発表をそのまま紹介してしまわれたのである. | |||
| と記し ([現代文庫版], p.187), 続けて |
| 初版が出たとき私はおもしろく読み, 誤りなどにも気づかなかった. 少し経ってから誤りを注意してくれた友人があり, 高木先生でも誤りをされることがあるのかと驚いた (中略). どんなに小さい問題に見えても, 高木先生がこの問題に挑まれたように, 真剣に考えねばならないことを示しているように思う. |
|||
| と記している (同書, p.188). [現代文庫版] にはこの問題に関して編集部による註が付されており (p.177), それによれば, \(n\!\not=\!2,6\,\)なる\(\,n\,\)次オイラー方陣の存在が1959年に証明されたという. 出典は記されていないが, 恐らく |
| [Parker1] E.T.Parker "Construction of some sets of pairwise orthogonal Latin squares." Proc. Amer. Math. Soc., Vol.10, 1959, pp.946–951. | |||
| [Parker2] E.T.Parker "Orthogonal latin squares." Proc. Natl. Acad. Sci. U.S.A., Vol.45, 1959, pp.859–862. | |||
| を根拠にしたものであろう. 単純な問題ながら, 数学史上において興味深い舞台を見せてくれる題材が, ここでも一つ追加されたのであった. |
| 貞治が74歳で上梓した最後の著作 |
| 高木貞治『數の槪念』岩波書店, 1949, 全94頁. | |||
| は,『新撰算術』,『新式算術講義』,『数学雑談』に引き続き, 数の構造を扱った著作である. 数の構造を究めることは, 貞治の (類体論と並ぶ) もう一つの重要な仕事であった. 貞治は, 生涯に亘ってこの問題から離れられなかったのである. |
 『數の槪念』(岩波書店, 1949) |
| その「序」は, 風変わりな書き出しで始まる. |
| うちの娘などは, 大學で理科を卒業したのだけれども, \(xy\!=\!yx\,\)など, どうしてさうなるのだか, よくわかつてゐないやうだ.
このやうに, エドムンド・ランダウは, 其の著『解析の基礎』の中に述べてゐる. かうしたことは, うちの娘たちに限るまいから, 一般讀者のために, 解析の基礎として, 數の槪念を, 根本から, 論理的に無缺陥なる體系として, 展開して見せようといふのであらう. |
|||
| 最初の一文は「うちの娘」\(=\)「貞治の娘」を想定させるが, 次の一文で「ランダウの娘」のことだと分かる. すなわち, 数学者シェーンベルク (Isaac Jacob Schoenberg, 1903-1990) と結婚した長女シャルロッテ (Charlotte, 1907-1949), および, 医者 (インディアナ大学医学部教授) になった二女スザンヌ (Susanne, 1908-1982) を指すのであろう. 娘たちも一般的な数学に関しては十分に理解していたと思われるが, とは言え, 基礎論の専門的レヴェルまで要求するのは流石に酷であろう. このランダウの言葉を受けて, 貞治は次のように述べる. |
| 今日, \(xy\!=\!y\!\:x\,\)にしても, \(\sqrt{2\,}\!\cdot\!\sqrt{3\,}\!=\!\sqrt{6\,}\,\)にしても,
周知であらうが, それが何故に然るか. 叉如何にして, それが證明されるか, といふことになると, 話は別である. しかし, 解析學を學ぶものは,
いつか一度は, 根本に立ちもどつて, 數學知識の再檢討をしてみる必要のあることは, 言ふまでもあるまい. さうして, そのとき第一に遭遇するのは, 數とは何ぞやといふ問題であらう. (中略) この問題を平易周到に解説することが, この小册子の目標である. |
|||
| 貞治は, この著作において, (自然数ではなく) 整数の公理から始め, 加法や乗法, 結合則や分配則などを示す. 次に有理数を構成し, 四則およびその稠密性を解き明かす. 最後に, 有理数による収斂数列の極限として, 加法公理を認めた一次元連続体として実数を構成するのである. ヒルベルトの幾何学基礎論における無矛盾の公理系を受けて, 貞治は整数論における無矛盾の公理系を追究した.「序」の末尾には次のように記される. |
| 無矛盾性の證明.「そんなことができるものか」(So was kann man ja nicht.) と, ランダウは勇敢に言ひ放つ (出所上掲). 吾々は謙虚な態度で, そんなことのできるのを待つてゐる. それができた上で, どんなものができたか, ゆつくり檢討することにしても, 晩くはあるまい, と思つてゐるのである. | |||
| 『數の槪念』と同年に出版された |
| 高木貞治『數學の自由性』考へ方硏究社, 1949, 全128頁. | |||
| は, 1936年から1944年にかけて執筆した数学評論ないし随筆を一冊に纏めたものである. これらの初出は, 藤森良蔵 (1882-1946)
主宰による数学誌『高數硏究』(考へ方硏究社) および受験雑誌『考へ方』である. |
 『數學の自由性』(考へ方研究社, 1949) |
| 貞治による「序」と巻末には藤森良夫 (良蔵の長男) による「高木貞治先生への感激」なる一文がある. ここには, 戦後『考え方』に発表された「數學の自由性 」および「考へ方のいろいろ」のほか, |
| ・數學漫談――わたしの好きな數學史 (第1卷第1號, 1936.10, pp.3-4) ・數學漫談――彼理憤慨 (第1卷第1號, 1936.10, pp.4-5) ・數學漫談――微積の體系といつたやうなこと (第2卷第3號, 1937.12, pp.1-4) ・Newton. Euclid. 幾何讀本 (第3卷第4號, 1939.1, pp.1-5) ・日本語で數學を書く, 等々 (第4卷第1號, 1939.10, pp.2-4) ・數學の應用, それの實用性などといふこと (第5卷第1號, 1940.10, pp.1-4) ・或る試驗問題の話 (第6卷第1號, 1941.10, pp.1-3) ・昔と今 ―― 圓周率をめぐつて (第7卷第1號, 1942.10, pp.1-10) ・數學の辻説法 (第7卷第8號, 1943.5, pp.1-2) ・數學の實用性 (第7卷第11號, 1943.8, pp.1-5) ・蟲干し (第9卷第1號, 1944.10, pp.39-42) |
|||
| が掲載されている (括弧内は,『高數硏究』掲載関連情報). 『高數硏究』は, 1936年10月から1944年12月まで発行された月刊誌である. 第1卷第1號の冒頭において, 藤森は「發刊の辭」に続き,「高數硏究發刊の趣意」として, |
| (前略) 昭和維新の達成が獨創發明の完遂にまつ以上, (中略) どうしても具現しなくてはならぬことは, 高等數學としての微積分を知つてゐる人を,
中等數學としての代數幾何を知つてゐる人の數位に到達せしむる事である. (中略) 高等數學入門, 大學數學解放をスローガンとして雜誌「高數硏究」を創刊することにした. |
|||
| と, かなり困難度の高い目標を掲げている (p.2). その内容については, |
| (前略) 高等數學の平易化, 大學數學の解放を目標として本誌を發行する次第でありますが, 高等數學をやるといふ以上, 何と云つても高等學校程度としての高等數學
―― 解析幾何, 微積分或は高等代數, 三角法といふものに對するしつかりした根柢を作つておくことが大切であります. (中略) 卷頭の論說としては, 日土大學講師諸先生並びに其他の権威ある方々から原稿を頂き, 明快且つ嚴密なる數學の眞の姿に接すると同時に, 數學を學ぶ者への正しき指針を示して頂くことになつて居ります. |
|||
| とある (p.2). ここに登場する「日土大學」は, 藤森が創設した一般人を対象とする講座である. |
| [高木末綱]『高木末綱兩博士を圍む日土大學座談會』/ 考へ方研究社『高數硏究』第6卷第11號 (1942年8月), pp.26-35. | |||
| を見ると, 貞治や末綱を中心とする数名が, 日土大学の現状と今後の在り方を論じている. 正規の大学生ではないが大学の数学に興味を有する一般人を相手に, 入門的な講義をなすことが目的であったらしい. 余談ながら, この座談会の中で, 次節で触れる矢野健太郎 (1912-1993) の名が現れる. |
| 藤森良蔵:矢野健太郎君なんかずつと始めから日土大學をきいてゐて, 去年日土大學の先生になつて非常にしつくりした講義が出來たといふことは, やはり會員の心理狀態を知つてゐるからですよ.
(後略) 高木:矢野がいつ聞いたんです? 藤森良蔵:新制にならない前からずつと聴いて居られたんです. 高木:君のところと關係があるんですか? 藤森良蔵:ええ, 雜誌の懸賞問題なんか熱心にやつてをられました. (中略) 藤森良夫:(前略) 川上圭介といふ人は, 丁度矢野君と同じくらゐの年配だ (中略). 高等學校の準備時代に「考へ方」の懸賞問題を熱心に應募したんです. (中略) 矢野君はその川上君達と一緒だつたんですから, その賞を互ひに爭つたものなのです. (中略) |
|||
| 貞治が定年退官した1936年当時の矢野は大学院生であり, この座談会が開かれた1942年当時の矢野は30歳で東大の講師であった. 掛谷や吉江などの同僚に対しては「君」づけにしていた貞治が, 学生ないし講師であった矢野に対しては呼び捨てにしている点が注意を引く. さて, 上記引用部にある「権威ある方々から原稿を…」の通り, 続く3頁から5頁にかけて,『數學漫談』と題する貞治の随筆が二つ (『わたしの好きな數學史』,『彼理憤慨』) 掲載されている. 『數學の自由性』の「序」を見ると,「『高數硏究』及び『考へ方』に掲載された雜文に多少筆を加へたものの集錄」とある. この著作の標題の由来でもある最初の小論『數学の自由性』(pp.1-16) では, カントールの言葉「數学の本質はその自由性にあり」が数学史上において如何なる状況で発せられたか, その経緯が具体的に示される. 後半部では, 数学史上に発生した順序そのままに学んだ貞治自身の学生時代にふれ, それは伝統に縛られた不合理な方法であると解く. 続く『考へ方のいろいろ』(pp.17-22) では,「ゼノンの逆説」の解説および時計の針が重なる時刻に関する軽い話題が展開される. 貞治の言う『わたしの好きな數学史』(pp.23-25) は,「正確なる史實の記錄」である. しかし,「(數学) 史論は各人各樣でなければなら」ず, 貞治は「面白い史論」を好むという. 貞治はこう述べた数年後に,「面白い史論」としての『近世数学史談』を自ら執筆したのであった. 『彼理憤慨』(pp.26-29) では,「極限だの収斂だの」に「構わ」ず「\(\displaystyle{\sqrt{\!\:1\!+\!x\,}\!=\!1\!+\!\frac{x}{\!\:2\!\:}}\,\)でよい」としたペリー (Matthew C. Perry, 1794-1858) の姿勢を引き, その「核心」である「數学の實用性」について,「人生は短いけれども, 多くの實用主義は人生よりも短命である」と述べる.「微に入り細を穿つよう理論を講ずる學術主義」や「理論を無視した極端なる實用主義」を斥け, ペリーが狙う数学教育改良講壇に関して, 貞治は, 彼らの抱く高遠な理想へ徐々に収斂することを信じると楽天する. ペリーは憤慨するが, 貞治のような「樂天家は憤慨しない」のだという. 『微積の體系といつたようなこと』(pp.30-39) は, 全篇中, 最もユーモアに富んだ逸品であろう. これも,『高數硏究』第2巻第3号においては『數學漫談』と銘打って掲載された. 内容は, 解析学における基礎的な話題であるが, 上記の矢野健太郎との関連で次節 (§6-2) で触れる関係上, その内容を少し詳しく見ておくことにする. なお, 初出の『高數硏究』と単行本『數學の自由性』とでは, 表記や内容に関して若干の異同がある. ここでは前者からの表記を採用しよう. |
| 本誌の爲に何か書けと, Nにせがまれ出したのは, 何でも蘆溝橋の頃であつた.「何分, この暑さではね.」で, あつさり撃退した積りでゐたのが, 不覺であった. 逆が必ずしも眞でないことを知らぬ顔に,「昨今は大分秋らしくなりました」ことを指摘するNである. 形勢は宜しくない. | |||
| 冒頭部において貞治はこのように記す. 藤森良蔵は貞治にたびたび『高數硏究』への寄稿を依頼した. とは言え, この著書において初登場となる頭文字「N」なる人物が誰なのかは判らない. |
| 形勢は單調に惡化した. 竟には「書くことがないから, 書かない」などと, 丸で借金の言譯でもするやうな破目に陥つた. しかしながら, 僕といへども, 日本男児のはしくれだ. 外交が下手で, 借りもしない借金を背負込むやうだが, かうなれば潔よく自腹を切つて見せようと, 決心をして居たのである. | |||
| 数学とは何の関連もない「漫談」が続くが, ほかでもない, 貞治の「漫談」であるからこそ, 読者は飽くことなく読み進められるのである. |
| それは小春日和の或る午後であつた. このやうな條件の下に於て, 僕の場合, 一般的には, 慢讀は甘睡に收斂するのであるが, 上記午後は特異であつた. 僕はハツとした, ハツとして發見をした. 借金を返す工面がつきさうなことを發見したのである. | |||
| これまで, 驚嘆すべき理論や美しく鮮やかな解法を展開した際にも決して大風呂敷を拡げなかった貞治が, ここでは些か昂奮ぎみに読者の注意を引いている. 以後, 例の「N」と, もう一人の人物「O」との対話形式で話は展開される.「O」は, 自宅で雑誌の整理をしつつ何気なく頁を捲っていて「ハッとした」のだという. |
| N.朝寝の後に晝寝, その忙がしい中で, 何をページつて, 何を發見したのですか. ――これですか Mathematische Zeitshrift, 40. 一つの連續函數について. Hermann Schmidt. Jena の住人. ページ70-71. こんな短いもので, 逃げようと言ふのですか. |
|||
| 会話の発端は, ドイツの数学誌に掲載されたシュミット (Hermann Karl Schmidt, 1902-1993) の論文 |
| [Schmidt] H.K.Schmidt "Über die Stammfunktion einer stetigen Funktion" Mathematische Zeitschrift, 1936, pp.70-71. | |||
| である. |
 シュミット『連続関数の不定積分について』冒頭部 |
|||
| 要は,「微分積分学の第一基本定理」即ち「有界閉区間\(\,I\!=\![\!\:a,b\,]\,\)で\(\,f\!\:(x)\,\)が連続ならば, \(I\,\)において連続関数\(\,F\!\:(x)\,\)が存在して\(\,F^{\prime}(x)\!=\!f\!\:(x)\).」(定理 (A) とする) の証明法に関する話題である. |
| O.何の變哲もないやうだが, S君はそこに變哲を發見したのだ. S曰く, (A) は問題としては微分學!の問題だ. (中略) この微分學の問題を解くのに, 現今はリイマン積分の可能性といふやうな積分學の定理を用ゐて大迂回をしてゐるのが, 心持が惡い, とSは言ふのだ. ビ分のことはビ分でせよ, と修身で敎はつたではないか! そこで, S氏は某年某學期に, 初級生の爲の講義に於て, 定理 (A) を微分學で說明したさうである. |
|||
| 『ヒルベルト訪問記』と同様, ここでも「S君」が登場する. この場合の「S」は, 言うまでもなくシュミットを指すものである. [Schmidt] の冒頭部 (上掲) を見ると,「任意の連続関数\(\,f\!\:(x)\,\)は原始関数\(\,F\!\:(x)\,\)の微分と看做せる」なる定理は, 本来は微分の範疇における証明が望ましい, これに基く1934年の夏学期の初心者向けに行った講義の内容を紹介したい, とある. 無論, ここには,「大迂回」が「心持が惡い」とか「ビ分のことは…」云々なる文言は見られない. 当時のドイツに「修身」なる授業があったかどうか, 私は知らない. これらは貞治流のユーモアであろう. |
| N.あゝ分かりました. あれでせう. 微分學と積分學, 神奈川縣と靜岡縣だ. 蘆の湖の水面にも神奈川縣と靜岡縣との境界がある. 境界がある以上は, 神奈川縣の鑑札を持つた船なら, 神奈川縣と蘆の湖の交はり, Durchschnitt に於て, 止まり, 走り, 叉は沈沒すべきである. 同樣に靜岡縣の鑑札……, 所で, その人, 靜岡縣の土木課ですか? O.氣の早い男だ. しかし, 何も箱根くんだりまで行かずとものことだ. 新聞で讀んだらう. 數寄屋橋の中程に行倒れがあると微分署と積分署との間に管轄爭ひが起るといふではないか, それは「おれは知らんぞ」といふのださうだが, Sの場合は (A) を微分署へ引取らうといふから, 殊勝ではないか. |
|||
| \(f\!\:(x)\,\)の連続性から, \(f\!\:(x)\,\)に各点収束する\(\,f_n(x)\,\)が線分の接続により得られる. 放物線の弧の接続として適当に\(\,F_n(x)\,\)を作り, \(F^{\prime}(x)\!=\!f_n(x)\,\)とできることは明白であろう. そこで,「項別微分の定理」すなわち「\(\,I\,\)で\(\,F_n(x)\,\)が各点収束し, \({F^{\prime}}_{\!n}(x)\!=\!f_n(x)\,\)が\(\,I\,\)で一様収束するならば, \(F_n(x)\,\)は\(\,I\,\)で収束し, その極限を\(\,F\!\:(x)\,\)とすれば\(\,F^{\prime}(x)\!=\!f\!\:(x)\).」(定理 (B) とする) を用いれば, 定理 (A) が得られる. なお, 些細なことであるが, 後に出版された単行本『數學の自由性』では, 上記の「N」の最後の台詞「同樣に……土木課ですか?」は削除されている (続く「O」の台詞にも若干の言い回しの違いが見られる). 一方, 上記の「N」台詞の冒頭には, 単行本において追加された台詞がある (下記の下線部). |
| N.あゝ分かりました. あれでしよう. sectionalism, 割拠主義というやつでしよう. 微分學と積分學, 神奈川縣と靜岡縣だ. (以下略) | |||
| この一文が追加された理由は不明であるが, これが発表された1949年当時 (戦後民主主義が発展しつつある中), 戦前に各地を席捲した軍閥割拠や国家レヴェルでの "sectionalism" を想起させることで,「嘗て流行した」即ち「現代にあっては時代遅れ」なるニュアンスを醸し出そうとしたのかも知れない. 何れにしても, 次節 (§6-2) でこの部分が引用される関係上, この追加された台詞の部分を附記しておく. |
| O.Sさんは連續函數の平等連續性と, よく知られた定理 (B) と, そんなものだけで, 積分なんかに觸れないで, 神奈川縣内に於て (A) に達したのだ. N.成程面白いですね. O.感心したらう. 所で定理 (B) だね. あれは, どうして證明するのだつたかなあ. (中略) \(f_n(x)\,\)が連續ならば, 積分をすれば, 直ぐに證明が出來る. Sの場合, 折角\(\,f_n(x)\,\)は連續だけれども, 不幸にしてその積分が封ぜられて居る. さうすると (B) の證明はむづかしい. (中略) S君は\(\,f_n(x)\,\)の連續性を利用して, 何かうまい考案があるのかな. |
|||
| 「O」自身はS何某氏が如何にして「定理 (B)」を証明したかに関しては知らないらしい. [Schmidt] では, 最初の頁 (p.70) の脚注において, [Landau] の「単純だが本書の中で最も難しい」という「定理344」が挙げられるのみである. ところがこの後, この「O」自身は, 積分せずに定理 (A) に達する方法があると述べる. 区間\(\,I\,\)の分割\(\,[\!\:x_{i-1},x_i\!\:]\,\)の最大値\(\,\mu_i\,\)を用いた\(\,\displaystyle{\small{\sum}\,\mu_i\!\:(\!\:x_i\!-\!x_{i-1})}\,\)は各分割に関して有界であるから, その下限\(\,S\,\)に対し, \(\,[\!\:a,x\!\:]\:(x\!\in\!S\!\:)\,\)における\(\,S\!=\!S\!\:(x)\,\)が\(\,I\,\)において確定する. これは連続で, 実は\(\,f\!\:(x)\,\)の原始関数になっているというのである. |
| N.當前でせう. 積分をすれば, 原始函数は得られませう. O.所が積分はして居ないのだ. 例の和\(\,\displaystyle{\small{\sum}}\,\)から極限へ行けば, それは積分さ. しかし吾々は極限へ行かなかつた. 吾々は下限へ行つて踏止まつた. 靜岡縣へ間一髪と言ふ所だね. (中略) Sさん曰く, あれは神奈川縣だ. 積分は確にして居ない. (中略) N.その下限と最大値とだけで, 原始函数を出すといふのは, 誰が考へたのですか. O.それは知らないね. Sは Landau の「手引き」に出て居るといふ. (中略) 出典調べにも及ぶまい. 旣に Vallée-Poussin の解析敎程に出て居る. あの爺さんなんか, 平氣なものだ. 連續函數の積分を定義する方法は, いくらもあるが, 最も手近なのは, 例の和卽ち\(\,\displaystyle{\small{\sum}\,\mu_i\!\:(\!\:x_i\!-\!x_{i-1})}\,\)の下限であらう. (中略) それを積分と名づけやう, といつた調子で, 心地よく, ドライヴ・ウエイをしてゐる. 縣の境界なんか無視して (後略) |
|||
| ここに現れるランダウの「手引き」とは前掲の [Landau] すなわち『微分積分学入門』であり, ヴァレ・プサン (Charles-Jean de La Vallée Poussin, 1886-1962) の『解析教程』とは |
| [Vallée Poussin1] de L.V.Poussin "Cours d'analyse infinitésimale Tome I" A. Uystpruyst - Dieudonné, 1903, 全372頁. | |||
| [Vallée Poussin2] de L.V.Poussin "Cours d'analyse infinitésimale Tome II" A. Uystpruyst - Dieudonné, 1903, 全440頁. | |||
| である. 以上が, 初出誌『高數硏究』に掲載された記事である. ところで, 以上の内容のみであるならば, 標題『微積の體系といつたやうなこと』の趣旨が判然としない. そこで『數學の自由性』pp.37-39 を見ると, 以上の記事に続けて, 後に追記された貞治の所見が掲載されている. 以下, そこから引用しよう. まずは,「微分, 積分」の名称についてである. 明治時代以降,「微分法, 積分法」と称していたものが, いつの間にか「微分學, 積分學」なる名称が流布していることを貞治は疑問視する. 英米ではこれらを一括して "calculus" と呼ぶ. これに倣って我が国でも「微分積分法」あるいは「微積」でよい, と述べるのである. 続いては,「微積分の體制」すなわち「初學者」へ「微分積分の手引き」をする手段についてである. 貞治は, |
| 微分と積分とを切り離し叉は對立させて,「微分のことは微分でする」といような考え方は不適切であろう (中略) 兩手ですれば具合よくできることを强いて片手でしてみたり, 兩足でらくに歩けるのを片足で跳ねて行くというようなことは, 特別の理由がない限り, 無益な難行苦行といふものであろう. S氏の指摘したことはたしかに面白い. 微分學の先生を喜ばせるに十分であろう. 喜ぶのはよいが, それを直に敎養學部の講義でやつてみるのは行き過ぎというものだ. そういうやり方を例の彼理などは批難するのだ. |
|||
| と述べる. これが貞治の主張したかった「微積分の體系」であった. 『解析概論』を執筆する中で, 貞治はその叙述法に関して種々の工夫を凝らした.「教本式」か「講義式」か, 歴史の流れに沿う形か, 天下り式を含む効率主義的な形か. 何れの形態を選ぶかは, 時代に趨勢に沿った執筆目的や出版事情その他の要因により左右される. 「一般向きの解析学予修書」ないし「解析学読本」として執筆された『解析概論』において, 貞治は, (上記の定理を含め) 可能な限り平易で単純な手法を採用したのである. 時代の変化の中で後に批判に晒されることになるのも想定済みであったことであろう. 『微積の體系といつたようなこと』のような「O」と「N」との対話形式は, その後も『Newton. Euclid. 幾何讀本』(pp.40-50),『應用と實用』(pp.64-71),『或る試驗問題の話』(pp.72-78) などで採用される. 落語を聴くかのような丁々発矢の遣り取りが読者を惹きつけて離さない. 無論, 内容に関しても, 数学史上における逸話 (『Newton. Euclid. 幾何讀本』(pp.40-50)), 数学用語の名称 (『日本語で數學を書く, 等々』(pp.51-63)), ガウスやフーリエによる計算の工夫例 (『數學の實用性』(pp.104-118)),『蟲干し』(pp.119-128) など, 読者を感心させる話題が豊富である. このガウスによる計算例は,『近世数学史談 3版』p.45 にあるものと同一である. その紹介の後, 貞治は |
| ガウスの手に掛かると, 整數論が實用的になる. 若しも吾々がその眞似をして, 何か妙案はないかなどと考へていた日には,「下手の考え休むに似たり」で,
時間の徒消に終るでしよう. それは不實用の極端でありましよう. ガウスの話をしたのは, 實用は物に在らず, 人に在り. 徹底的なる理解の上に於てのみ, 眞の實用は可能である, ということの一例を擧げたのであります. 吾々凡人にはガウスの眞似は出來ない. しかしガウスの精神を眞似ることは出來る. (中略) 世ニ用アリヤ, ナシヤなどと大それたことを考えないで, 身分相應の所で最善を盡くすこと. これが吾々に與えられたる唯一の途でありましよう. |
|||
| と結んでいる (p.118). 現代においても「数学の実用性」を云々する者達は少なくない. その多くは, 概して数学に対する無理解 (苦手意識を纏った)
者達である. 貞治のこの見解を是非, 味わって頂きたいものである. この著書の中では,『昔と今 ―― 圓周率をめぐつて』(pp.79-99) が興味深い. 円周率の計算は, 実用的な必要性もあって, 古代から多くの人々の興味ある対象であった. アルキメデス (Archimedes, 紀元前287-212) は正九十六角形の周を考察して\(\,\displaystyle{3\frac{1}{\!\:7\!\:}\!>\!\pi\!>\!3\frac{10}{\!\:71\!\:}}\,\)を得たという. また, マチン (John Machin, 1680-1751) は, 初等的ながら極めて巧妙なる計算によって得た |
| \[\displaystyle{\frac{\!\:\pi\!\:}{4}\!=\! 4\mathrm{Arc}\tan\frac{1}{\!\:5\!\:}\!-\!\mathrm{Arc}\tan \frac{1}{\!\:239\!\:}}\] |
|||
| を用いて小数点以下100桁まで計算したという. 貞治は, このマチンの公式を, \(\displaystyle{\frac{1}{\!\:1\!+\!x^2}}\,\)の冪級数展開の\(\,0\,\)から\(\,x\,\)までの項別積分\(\,\mathrm{Arc}\tan x\,\)から |
| \[\,\displaystyle{\tan\!\left(\!4\mathrm{Arc}\tan\frac{1}{\!\:5\!\:}\!-\!\frac{\!\:\pi\!\:}{4}\!\right) \!=\!\frac{1}{\!\:239\!\:}}\,\] |
| を用いて得る方法を紹介している. |
|
\(\,\displaystyle{}\,\)シャンクス (William Shanks, 1812-1882) もこの公式を用いて707桁まで計算したが, 第528位以下に誤りがあったことが後に判明したようである
(『數學』第1卷第1號, 岩波書店, 1947, p.45). |
 『数学』第1巻第1号 p.45 掲載記事 (執筆者不詳) |
|||
| また, オイラー (Leonhard Euler, 1707-1783) は, 極めて技巧的なる計算によって得た |
| \[\displaystyle{\frac{\!\:\pi\!\:}{4}\!=\! 5\mathrm{Arc}\tan\frac{1}{\!\:7\!\:}\!-\!2\mathrm{Arc}\tan \frac{3}{\!\:79\!\:}}\] |
|||
| を用いたが, マチンよりもうひと工夫を加え, 収束するスピードの速い |
| \[\displaystyle{\frac{\!\:\pi\!\:}{4}\!=\! \frac{7}{\!\:10\!\:}\left\{\!1\!+\!\frac{2}{\!\:3\!\:} \!\cdot\!\frac{2}{\!\:100\!\:} \!+\!\frac{2\!\cdot\!4}{\!\:3\!\cdot\!5\!\:} \left(\!\frac{2}{\!\:100\!\:}\!\right)^{\!\!2}\!\!\!+\!\cdots \!\right\}\!+\!\frac{\!\:7584\!\:}{\!\:10^5\!\:} \left\{\!1\!+\!\frac{2}{\!\:3\!\:}\left(\!\frac{144}{\!\:10^5\!\:}\!\right) \!+\!\frac{2\!\cdot\!4}{\!\:3\!\cdot\!5\!\:} \left(\!\frac{144}{\!\:10^5\!\:}\!\right)^{\!\!2}\!\!\!+\!\cdots \!\right\}}\] |
|||
| を得てから円周率を計算した. 貞治は, このオイラーの手法に関して, 10の冪を分母に含めた点に「實用整數論」的手腕を認めている.「一寸眞似の出來ない藝當で, アルキメデスの再生とも言うべき所」と賞讃する (p.90) のである. 数学史上における円周率の計算技法の向上に関しては, 現代では既に数多の解説書が出版されているが, これが人口に膾炙していなかった時代にあって,『數學の自由性』は多くの読者の興味を掻き立てたことと想像される. 周知の通り, 現在でも小数点以下の桁数の記録は日々更新され続けている. コンピューターの機能性を図る指標とされることもあるが, 如何に収束スピードの速い級数を得るかが本質的な重要性をもつと言えよう. ラマヌジャン (Srinivasa Ramanujan, 1887-1920) が考案した円周率に関する数々の驚異的な公式は現代ではよく知られている. 直近では, 高速で収束するアルゴリズム (チュドノフスキー法による級数) |
| \[\displaystyle{\frac{1}{\!\:\pi\!\:}=12 \sum_{k\!\:=0}^{\infty} {\frac{(-1)^k (6k)!\,(545140134\!\:k+\!13591409)}{(3k)!\,(k\!\:!)^3(640320)^{3k + 3/2}}}}\] |
|||
| を用いて202兆桁まで計算されているという (2024年6月28日現在. 米国の Wikipedia による). 閑話休題. 現在,『數學の自由性』は絶版であるが, 現代仮名遣いに改められた |
| 高木貞治『数学の自由性』筑摩書房 (ちくま学生文庫), 2010, 全346頁. | |||
 『数学の自由性』(ちくま学芸文庫, 2010) |
| は入手しやすい. この [学芸文庫版] には, 前出の『過渡期の数学』,『中学時代のこと』,『明治の先がた』,『オイレル方陣について』のみならず,『訓練上数学の価値』(1936),『現代数学の抽象的性格について』など, 貞治の数学思想が現れた小篇が幾つも収録されている. |
| 本稿冒頭部において, 私が本稿を執筆する動機に関して簡単に述べた. 前掲書 [本田] (『高木貞治の生涯』(日本評論社『数学セミナー』1975年1~6月号) を執筆した本田欣哉 (1924-2018) は, これに関して次のように述べている. |
| 高木博士という人物は, 偉人ぶらず, 天才ぶらない点で, 終始一貫している. 84年の生涯を, '普通の人' として生きた (中略). 何の劇的波瀾も無く, 普通の人として坦々と生きながら, しかしその生涯のある時期に, 渾身の力をふるってひとつの masterpiece を生み出し, そしてふたたび, 坦々とした後半生を生きた. 博士の生涯には, 玄妙で豊かな味わいと, ひとつの美があり, それは数学者だけでなく, 一般の人々にも十分味わってもらうことができる (後略). |
|||
| 同様の記載は,『高木先生の伝記』(前掲書 [追想高木] p.182) にも見られる. 貞治は,『わたしの好きな數學史』(前掲) において「正確なる史實の記錄」を挙げた. とは言え, 本人でさえ,「正確」を期すことは容易ではない. 貞治自身, 先に引用した『中学時代について』のほか, 他の箇所でも |
| 過ぎ去ったことを正確に伝えるのは, 非常に難しい.『一数学者の回想』 回顧は老人の追想談になるのが普通で, それは通例不確かなものである『回顧と展望』 |
|||
| などと述べている (何れも冒頭部で言及されている). [本田] は, 直接的に貞治を知る多くの人物を取材し, 多くの記録を調査した労作であるが, 取材対象が (記事記録ではなく) 人間である場合, 上記の「記憶の不正確さ」は, 当然考慮されなければならない. 例えば, 幼少時代の貞治の神童ぶりを伝える『岐阜日日新聞』(1886年1月7日付) による「記事」として, [本田] には |
| 美濃国本巣郡数屋村高木勘助の長男貞治というは今年漸く10年1ヵ月と成り, まだ乳臭を離れざるも, 夙に一色小学校に通学し, 当時既に高等三級の学課を修め, 頗る穎才の天資なるに, 加ふるに映雪聚螢の勉励と師父教育の懇切にして, 大いに学業勇進し, 正科の外に更に英学を研究し, 愈よ奮発し怠らざるよし, 実に後世頼もしき神童なりと. | |||
| とある (『数学セミナー』日本評論社, 1975年1月号, p.16). 私はその原典『岐阜日日新聞』を確認していないが, このような公的な「記事」に関しては, 誤謬は少ないと考えられる. 尤も, 引用者側にミスが生じることはあり得る. 上記引用部には一部に旧字や旧仮名遣いが見られる (恐らく修正洩れであろう) が, 当時の新聞は全般に亘って旧字および旧仮名遣いで表記されていたことと思われる. 一方, 大学時代の貞治の秀才ぶりを伝える八田三喜 (1873-1962) による「伝聞」として, [本田] には |
| 微積分の試験の前に, 本多光太郎 (後年, 鋼鉄の研究で文化勲章を受賞) が友だちに向かって,「俺はノートを4へんよんだから, どこから出てもいい」というと,
高木が皮肉な微笑を浮かべて,「数学って, 暗記する学問ですかね」といった. ガムシャラに勉強する本多の善良性へのこの皮肉は, 高木の現代人的な知的な性格を,
鮮明に示しているのである. ところで, この藤沢の試験の結果であるが, 高木の成績は140点であった. もちろん, 100点満点なのである. この点数は, 高木の数学的頭脳の冴えを示すとともに, その冴えを敏感にキャッチして, かつそれを独特の流儀で表現した, 藤沢の頭脳と性格をも示しているのである. |
|||
| とある (『数学セミナー』日本評論社, 1975年2月号, p.34).「受賞」なる記載がミスであることは直ぐに気づくが, 八田三喜の記憶までは検証できない. 藤沢か本多または貞治自身の述懐があれば話は別であるが,
私自身はこれに関する他の文献を寡聞にして知らないのである. 本田が八田からこの逸話を聞いたのがいつであったかは記載されていないが,「高木と大学時代のはじめ同級であった八田三喜氏と, 筆者はその生前インターヴィューをすることができた. (その後, 昭和37年, 89歳でなくなった.)」と記載されている. 従って, この記事が『数学セミナー』に発表された時点では, 誰もこの逸話を検証できない状態にあったわけである. なお, 本田自身はこの逸話がお気に入りであったようで,『100人の数学者』(数学セミナー増刊, 日本評論社, 1989, p.178) や『高木貞治の生涯』(『数学セミナー』日本評論社, 2010年3月号, p.10) でも (各々異なる私見を交えながら) 紹介している. 伝記ないし評伝を書く際には, 多くの困難を伴う. これは, 筆者が特定の人物に興味関心をもつがゆえに執筆されることが多い. その場合, 多かれ少なかれ, そこには筆者の感情 (畏敬や崇拝, 憧憬や憐憫, ときには軽蔑や嫉妬など) が含まれることになるであろう. 人物を評価する場合, 過小評価することは無論避けるべきであるが, 過大評価することも避けるべきであろう. 性格や業績に見解を挟む場合にも, 矛盾が生じないよう, 注意を払う必要がある. 本田は, 貞治を「偉人ぶらず, 天才ぶらない (中略) 普通の人」と評する一方で, 上記の例を引いて「本多の善良性へのこの皮肉は, 高木の現代人的な知的な性格を, 鮮明に示している」と評している. 前者の評価については, 特に異論はない. 後者の評価おける「善良性への皮肉」なる表現が気に掛かる. 本多の言う「ノートを4へん読んだから」云々は,「試験範囲における数学を丸暗記した, または当該箇所の論理の要点を完全に理解した」の意味であろう. 貞治は,「数学は暗記によって理解する (し得る) とする考え方や姿勢」を穏やかに批判したのであろう.「ガムシャラに勉強する本多の善良性」とは, 何事に対しても成り振り構わず懸命に努力する本多の性格を指すものであろうか. 貞治は, 本多のそのような部分を,「皮肉」ったのであろうか. この点に些か疑問が残るのである. さらに,「この皮肉」が「現代人的な知的な性格を (示し)」なる表現も気に掛かる. これを読む限りでは, 具体的に如何なる状態を指すものかが判然としない. 具体性のない「何か」をもって貞治を無意識の裡に過大評価する仕儀に陥っていないであろうか. 「100点満点」中, 如何なる理由で「140点」であったかに関して八田の言明はなかったにも拘らず (あったならばこれも記載すべきであろう),「高木の数学的頭脳の冴え」あるいは「独特の流儀で表現した, 藤沢の頭脳と性格」云々に関しても, やや憶測が過ぎるように思う. 仮に, 貞治がこれを読んだとしたら, 何と述べるであろうか. 私自身は,「高木の成績は140点」なる逸話に関しても貞治ならば「それは正確ではない」と否定するかも知れない, などと憶測する者である. 一方, 河田敬義は, この種の逸話の取り扱いには慎重な姿勢を見せている. [追想高木] 所収の『追悼会での思い出ばなし』(pp.207-210) では, 貞治が逝去した翌年に開催された内輪の追悼会の席上で遺族や関係者から語られたことが記されている. ただし,「録音したのではないから, 不完全なものであり, 聞き誤りもあったかも知れない. また, 多くの方々はすでに亡くなられたので, 確かめることもできないままである.」とある. 河田敬義の誠実さが伝わる文章である. ちなみに, 河田自身の人となりについては, §4-9.における前掲書『柔らかい頭と強腕 河田敬義追想集』(1994) に詳しい. 因みに, この『思い出ばなし』には, 末綱恕一や守屋美賀雄 (1906-1982), 菅原正夫や黒田成勝などの教え子達による |
| 末綱 Klassenkörper を類体と訳されたのは高木先生であった. 私は共立社の講座を書くときに級体としたが, 先生の気に入らなかった. これは後の類数 (Klassenzahl) という訳とも関連していた. | |||
| 守屋 Bewertung を賦値と訳したのも先生であった. | |||
| 菅原 大学を卒業したとき, 先生から数学が分かったかと言われて返事に困った. いくらか分かったような気がすると答えたら, 先生はそれは嘘だ, もっと具体的な問題からやり直せと (後略) | |||
| 黒田 ブロウエルの論文を読んで, 初めの集合の定義が分からなくて, そう言ったら, 先生もよく分からないと言われたことがあった. | |||
| などの回想が語られている. また, 貞治の門下生の一人で類体論を深く理解している彌永昌吉は, 貞治の「ガウス数体の上の相対アーベル体がすべてルジャンドルの楕円関数の特殊値で生成せられる」ことを示した学位論文を紹介する文脈において, |
| 後の御仕事をも合せ考えれば, 先生はこの時すでに一般相対アーベル体の理論について重大な予想を持っておられたのではないかと想像される. 然るに先生はその後約10年間,
一つも論文を出されなかった. (中略) 先生は先生としての夢を育みつつ, 徐ろに想の熟するのを待たれたのであろう. (中略) あくせくと仕事をし, 焦り気味に発表する多くの学者とは, 全く正反対の行き方である. 先生の落着いた, 自ら深く信ずるところのある, 迫らない御性格によってのみ, 始めてこのようなことができたのである. |
|||
| 記したことがあった (前掲書 (§3-7) [彌永8], pp.8-9). この記事の初出は『帝大新聞』(1940年11月発行) であり, この文章は恐らく貞治の目にも止まったのであろう. その直後 (1940年12月7日) に開催された講演『回顧と展望』において,「類体論は主として第一次世界大戦の「刺戟」によって始められたので, そう前から考えていたのではない, と述べられた」ことを受け, 彌永は次のように追記した (同書, pp.11-12). |
| 勝手な想像で書いたりしたことを, 申し訳なく思った (中略). これが, 先生を冒瀆することにならねばよいが, と私は気遣っている. ただ心中いつも先生に頼っている一人の書いたもののこととて, わりなきふしもあらば, と御諒恕あらんことを, 先生および読者にお願いするのである. | |||
| 彌永は貞治を尊敬するあまり, 理想化した憶測を加えてしまったのであり, 他意があったわけではない. それを理解しつつ, それでも自身に対する過大評価を看過できない貞治は, 講演においてその憶測を修正したのであった.「偉人ぶらず, 天才ぶらない」というよりも, 事実を正しく認識し, また認識してもらおうとする貞治の科学者的な姿勢が, このようなところに如実に現れていると言えよう. 一方, 上記のように自身の誤りを詫びる彌永に見られる謙虚な姿勢にも感心させられる. 些細なことながら, 上記『回顧と展望』の講演日を「12月7日」と記したのは,『近世數學史談』[第2版] (1942) の記載によるものである. [第3版] (1971) や直近の [岩波文庫版] (1995) に至るまで, この日付に異同はない. 一方, 初出の『高數硏究』(§2-1 において紹介した [速記版]) には, その前日「12月6日」なる記載が見られる. ところで, 過大評価されることを好まなかった貞治は, 過小評価されることに関しては如何なる判断を下したであろうか. 「高木関数」を知らなかったランダウがファン・デル・ヴェルデン (Bartel Leendert van der Waerden, 1903-1996) の構成した関数を高く評価した件 (§4-9) について, 貞治が何か批判した様子はない. 後年,『解析概論』の当該箇所では, 淡々と事実を述べたのみであった (p.471). ランダウにとって, 相手が貞治であったことが幸いした. これがルジャンドルやコーシーであったら, ランダウは彼らに罵詈雑言を浴びせられたことであろう. 類体論の概要を発表した時点では, 貞治の理論は誰にも理解されず, 何の反応もなかった. これも一種の (主体性の無い) 過小評価と言えようが, これに関しても貞治がどこかで不満を洩らした形跡はない. 時が熟するのを待って, ジーゲルおよびアルティンに論文を送付したのみであった. |
| 他にも, (故意ではないが) 貞治に対する過小評価に繋がった実例がある. 私が最初にこの実例を知ったのは, |
| [梅田1] 梅田亨『「微分のことは微分でせよ」とは』/ 日本評論社『数学セミナー』2004年1~3月号. | |||
| によってであった. これは後に単行本化され, |
| [梅田2] 梅田亨『徹底入門 解析学』日本評論社, 2017, pp.2-23. | |||
| に収録された. 以下に述べることの要点は, 全てこの著作に掲載されている. 但し, (上述した理由で) 孫引きを避けるため, 私自身が確認できた範囲のものをここに記すことにする. 私が矢野健太郎 (前出, §5-6) の名を知ったのは, その著書 |
| [矢野1] 矢野健太郎『数学のたのしさ』新潮文庫, 1976, 全237頁. | |||
|
を読んだ中学3年生時のことであった (拙稿『楽しい読書・夏』(2009) 参照). 矢野には, 論文 (微分幾何学関連) の他に, 大学生用の数学演習書や高校生向けの受験参考書, 一般人向けの啓蒙書など,
夥しい数の著作があることはよく知られていよう. 矢野は1931年に東京帝大に入学し, 1934年に卒業した. その後2年間, 1936年までを大学院生として過ごした. 貞治の代数学の講義を学部時代に聴講している. 貞治が定年退官したのが1936年の3月であるから, 貞治の教えを受けた学生としては最年少の世代に属する. |
| [矢野2] 矢野健太郎『ゆかいな数学者たち』新潮文庫, 1981, 全293頁. | |||
| には国内外の数学者の興味深いエピソードが多数紹介されており, 貞治に関する逸話も10種類ほど掲載されている (pp.16-28). 代表的な逸話は, |
| [矢野3] 矢野健太郎『数学の散歩道』新潮社, 1972, pp.47-49. | |||
| [矢野4] 矢野健太郎『数学者のおくりもの』旺文社文庫, 1980, pp.268-269. | |||
| [矢野5] 矢野健太郎『数学者おぼえ書き』新潮社, 1980, pp.21-23. | |||
| [矢野6] 矢野健太郎『草履を拾っていただいた話』/ 前掲書 [追想高木] , pp.128-131. | |||
| などにも現れる. これらは一字一句同一ではないが, 大意については大同小異であるから, ここでは, 最も簡潔に纏められている |
| [矢野7] 矢野健太郎『東大で教えていただいた先生方の逸話』学士会アーカイブス, No.742, 1979. | |||
| から抜粋する. |
| あるとき高木先生は, この雑誌に1つの論文を寄稿された. それは, いままでは, 微分学の定理であるのに, 積分学を用いて証明されていた定理に対して,
微分学の範囲内での証明を与えられたものであった. そして先生はこの論文を, つぎの言葉で結ばれた.「昔から言うではありませんか. 微分のことは微分でせよと」 |
|||
| この最後の駄洒落は有名である (本稿においては, 前出 (§5-6) の『微積の體系といつたようなこと』(以下 [體系] と略記する) の項で引用済みである). 私のこれまでの勤務校においても, 年配の教員が, 微分に関する問題を質問しに来た生徒に対して (冗談としてではあるが) この駄洒落を発するのを何度か耳にしている. 但し, 私がこれを知ったのは [體系] によってではない. 学生時代に読んだ [矢野5] によってこれを知った. 単なる駄洒落として記憶されただけではない. 貞治が何か独創的な発想をもって画期的な証明を発表したらしいことも, 鮮明に私自身の記憶に残されたのである. 一方, 私が『數學の自由性』を繙いたのは [梅田1] を読んだ後のことである. 梅田の報告に驚愕し, それを確認するために初めて『數學の自由性』を手にしたのであった. ところで, これを孫引き (曾孫引き?) したと思われるのが, §4-9 において「名著」の一つとして掲げた |
| [赤1] 赤摂也『微分学+積分学』数学セミナーリーディングス, 日本評論社, 1973, 全224頁. | |||
| である. その「まえがき」は, |
| 本書は題して〈微分学積分学〉という. その内容は, 通常,〈微分積分学〉ないしはつづめて〈微積分学〉とよばれるものである. | |||
| なる書き出して始まる. これ自体は, [體系] において貞治が言及したものと同等の名称に関する話題であり, 特に問題はない. ところが, その後半には, |
| 〈微分学〉を〈積分学〉から全く分離し,〈微分学積分学〉と題したのも, 一にこの分野の理論構造をよりあきらかにしようと思ったからにほかならない.〈ビブンのことはビブンでせよ〉というのは高木貞治先生の名警句であるが, 私は, これを進んでそっくり頂くことにしたのである. | |||
| と記されているのである. これが, 貞治の意図と真逆であることは, [體系] を読めば明白であろう. そもそも, この句が (赤の言う意味での)「警句」として発せられたものではないことも [體系] を読めば分かるはずであるから, 赤自身はこれを読んでいない可能性が高い. であるならば, 赤の文言は, [梅田] p.2 にあるように「引用の孫引き・曾孫引き」ということになる. 出版年月から見て, 引用元の可能性があるのは, §4-9 においてやはり「名著」の一つとして掲げた |
| [一松1] 一松信『解析学序説 上』裳華房, 1962, 全342頁. | |||
| [一松2] 一松信『解析学序説 下』裳華房, 1963, 全316頁. | |||
| [一松3] 一松信『解析学序説 上 (新版)』裳華房, 1981, 全275頁. | |||
| であるか, または [矢野3] であろう. [一松1] における該当箇所 (第Ⅱ章 積分法) には,「基本定理」即ち「連続函数は必ず原始函数をもつ. 原始函数は, 定義域内の一点での値を定めれば, 一意的に定まる.」の証明に関して, |
| この定理はみかけ上は, 微分方の域に属するものであるが, 普通は積分 (定積分) を作って, それがちょうどうまく原始函数になっている, ことを証明する. (中略) 定積分の概念に依存せず, 微分法の範囲内だけで証明することも, まったく不可能ではない.*) しかしそれにはかえって不自然な技巧が必要なので, ここには採用しない. | |||
| とあり, 脚注*) を見ると, |
| かつて高木貞治先生が 'ビブンのことはビブンでせよ' という有名なシャレをとばしたものである. (数学の自由性, 考え方研究社, 1949, p.32; 同所に書かれた高木先生の意見には含蓄が多い.) | |||
| とある (pp.48-49).「ビ分」(貞治) でも「微分」(矢野) でもなく,「ビブン」(一松) と表記した点から見て, 赤による引用部は, 一松の上掲書からの曾孫引きである可能性が高い.
また, [一松2] における当該箇所「第X章 一様収束」を見ると,「定理10.7. (項別微分の定理)」に対する (\(\{f_n(x)\}\,\)の各点収束性と\(\,\{{f_n}^{\!\prime}(x)\}\,\)の一様収束性による) 証明が示された後に,「別証」が掲載されている. そこには, |
| 定理10.7 は文面上は微分法の定理であるから, 積分を使わない直接証明を与える.*) | |||
| とあり, \({f_n}^{\!\prime}(x)\,\)の連続性や可積分性を仮定しない証明が示されている. 脚注*) を見ると, |
| このような証明は, 単に sectionalism 的な 'ビブンのことはビブンでせよ', という興味だけではない. 定理自身の精密化, および後述のようにこれによって基本定理の一つの証明ができる点が重要なのである. | |||
| とあり, [體系] において貞治が紹介したシュミットの方法が「補題10.8. 基本定理 (連続函数は原始函数をもつ)」の証明中に紹介されている (pp.52-54).
一松が [體系] を読んでいることは疑いがない. 上記引用箇所に見られる "sectionalism" が単行本『數學の自由性』で追記された台詞であることは, 前節 (§5-6) において述べた通りである. 次に, これらの著作の改訂版である [一松3] を見てみよう. 配列や表記における (旧版に対する) 大幅な変更は, 恰も別の著作に見えるようなレヴェルの改訂である. 旧版では一変数と多変数で上巻と下巻に分別されていたが, 新版では実用的な話題と理論的な話題とで上巻と下巻に分別されたのであった. 余談ながら, 私自身は旧版の方を好んで読む者である. さて, 当該箇所「7. 級数・整級数」を見ると,「定理7.18. (実変数の項別微分の定理)」の証明の後の「注意」として, |
| 定理7.18 は, 形の上では微分法の定理であり, 積分を使わずに証明することも可能だが面倒である. 高木貞治先生の有名な言葉 'ビブンのことはビブンでせよ' は, 元来この定理に対するものであった. | |||
| と記載されている (p.192). 旧版では,「割拠主義をもって定理の精密化と基本定理の証明の一つが得られる点が重要」と述べた一松が, 新版では「積分を用いない証明は可能だが面倒」と片づけてしまっている. 因みに, |
| [一松4] 一松信『解析学序説 下 (新版)』裳華房, 1982, 全286頁. | |||
| には, この話題に関する記載は一切見られない. [梅田] においては, 矢野の事実誤認が厳しく責められる. 即ち, この駄洒落が発せられたのは, 論文においてではなく, 結びの文句でもない, 抑々この「新証明」自体が貞治の考案によるものではない, 等々. 矢野自身は, 後に単行本化された『數學の自由性』ではなく, この話題の初出である『高數硏究』における [體系] を読んだものと思われる.『數學の自由性』には「微分, 積分」の名称および「初学者へ微分積分を手引きする手段」に関する貞治の見解が追記されていることは既に述べた. 矢野の記述法を見る限りでは, 矢野はこの追記部分を読んでいないか, または, 駄洒落に気を取られるあまり (本質的な重要性を見落として) 失念してしまったかであろう. 元来, [矢野1] から [矢野6] までの一連の著作は, 数学を専門としない一般読者を対象として執筆されたものである. 一般的には, 堅苦しく気難しい性格をもつ別世界の存在と看做されている「数学者」を, ユーモアのある親しみ易い存在として紹介しようとした矢野の意向は充分に理解できる. しかし, とは言え, 人物の過小評価に繋がる事実誤認を看過するわけにはいかないであろう. 事実, これを受けての [赤1]「まえがき」における曾孫引きである. 原典を照合せずに貞治の一部の台詞のみを切り取って掲載した矢野および赤の責任は大きい (照合した上での誤解, 表記ミスの可能性もゼロではないが……). また, 原典を熟知していたと思われる一松による上記のような脚注も, やはり誤解を与えかねず, 全く責任がないとは言えないであろう. その結果, [梅田] (p.3) にある通り, |
| これらの引用文を見ると, 高木貞治は, (1) 微分学の定理はできるなら, 微分学だけで証明するのが望ましい (2) 或る微分学の定理に対し, 微分だけ使う証明を自ら工夫した ように見える. 上の引用は, もちろんこれを肯定的にとらえているが, 陰では逆に「高木貞治は解析学者でなく, 代数学者だからそんなセンスの悪いことをやったのだ」というアンチ高木の評価をしたり顔で述べる人もいる. |
|||
| となるわけである. 最後に言及される「したり顔で述べる人」が誰を指すものかは不明であるが, SNS 上における匿名の何某を指すものであれば, 私自身も該当者 (該当記載) を見かけたことがある. |
 梅田亨『徹底入門 解析学』(日本評論社, 2017) |
| これが貞治に対する過小評価の例である. これに関する貞治への誤解が拡散しないよう, [梅田] が人口に膾炙することを望みたい. 余談ながら, [梅田] は,「有界収束定理」および「フーリエ級数」に関する独自の視点による解説が収録された, 大変に興味深い著作である. また, 上記のような瑕疵は見られるものの, [赤1] も, 他にあまり類を見ない特異な構成法をもつ, しかし厳密且つ明快に書かれた名著であるという評価に変わりはない. 私自身が長年所属している数学研究サークル (現在も継続中) においても, 赤摂也の著書は概して評判が良い. このサークルでは, 嘗て, [赤1] 以外にも, |
| [赤2] 赤摂也『集合論入門』培風館, 1957, 全180頁. | |||
| [赤3] 赤摂也『確率論入門』培風館, 1958, 全224頁. | |||
| を, 各々, 一定期間を費やして講読したことがあった. いずれも, 省略や誤魔化しのない厳密かつ単純明快な論理構成に感心させられた著作である. 矢野にせよ, 赤にせよ, 原典を確認せずに貞治の台詞の一部のみを切り取って掲載したことは問題であったが, 根柢には彼らの貞治に対する畏敬の念が窺えるものであった. 記憶違いや多少の憶測が含まれることを前提して読むならば, 矢野による貞治に関する逸話は (他の数学者に関する逸話も含めて), 大変に面白い. 次の「NとO」に関する逸話も同様である. 再び [矢野7] から引用する. |
| 私より2年後輩の田島一郎君が「高数研究」という雑誌の編集をしていた. 高木先生は田島君から求められて, ときどきこの雑誌に面白い記事を寄稿された.
それらの一連の記事は, Nという人物とOという人物の対話の形をしていたが, Nが愚問を発すると, Oがそれをたしなめつつ, 詳しい数学的な説明を与えるという形をしていた. 田島君も私も, このNとOは何を意味するかわからなかったが, 恐る恐る高木先生に伺ったところ, このNは NANJI (汝) の頭文字で, Oは ORE (俺) の頭文字であるという先生のお答えであった. |
|||
| 『高數硏究』に現れる「O」と「N」については先述した (§5-6).「Nが愚問を発する」なる表現が適切かどうかはともかく, 先述した通り,「O」と「N」の間には, 読んでいて小気味よい「落語を聴くかのような丁々発矢の遣り取り」が交わされるのである. それらは全て, 貞治の優れた表現力の賜物にほかならない. 矢野は, この逸話に関しても他の複数の著書で紹介している. 上記の引用部を見る限りでは,「恐る恐る高木先生に伺った」のが誰なのかは不明であるが, [矢野2] によれば, 田島が貞治に尋ねたようである (pp.23-24). |
| あるとき田島君が,「矢野さんは先生の文章に出てくるNという名前をOという名前のいわれを知っていますか」と聞くので,「そんなことは僕には判らないよ.
高木先生に直接伺ってみたらいいだろう」と答えると, 田島君は,「そんなこと先生に聞いてもいいかな」と言っていたが, 思い切って先生に伺って,
しばらくすると私につぎのように教えてくれた. 「矢野さん. 判ったよ. 高木先生に伺ったところ, Nは NANJI (汝), Oは ORE (俺) の頭文字だってさ」なるほど, おかしなことを言うのは汝であって, これをたしなめるのは俺というわけであった. |
|||
| 一方, 矢野の『草履を拾っていただいた話』([追想高木] p.130) には,「私はこのNとOの意味がよく判らなかったので田島君にきいてみた. ところが田島君も知らないという.」とある. 田島から発せられた疑問なのか, 矢野から発せられた疑問なのか, という点に関して, 両者の記載内容には矛盾が生じている. 些細なことであるが, 矢野の複数の著作には, 同一の逸話であってもこの程度の差異 (少なくとも一方は事実と異なる記事) が見受けられるのである. 『高數硏究』にたびたび原稿を依頼していた田島がNとOの謂われに関して尋ねたのだとすれば, 田島自身も何かの折にこの話題に触れていそうなものである. しかし, 彼の著作は, 私が知る限り, 純粋な数学書 |
| [田島1] 田島一郎『数学解析入門』好学社, 1960, 全258頁. | |||
| [田島2] 田島一郎『整数』(数学ワンポイント双書10), 共立出版, 1977, 全96頁. | |||
| [田島3] 田島一郎『イプシロン-デルタ』(数学ワンポイント双書20), 共立出版, 1978, 全128頁. | |||
| [田島4] 田島一郎『解析入門』(岩波全書325), 岩波書店, 1981, 全293頁. | |||
| のみであり, この逸話に触れた田島の随筆ないし評論を見かけたことはない. 余談であるが, [田島1] p.151 および [田島4] pp.162-165 には,『高數硏究』からの引用 (前者は吉江琢兒, 後者は彌永昌吉による) があり, 読んでいて大変に面白い. とは言え, この逸話が矢野自身の創作 (想像) のみで書かれたわけではないであろう. 上掲した [矢野1] から [矢野7] が出版 (発表) された時点では, 田島はまだ存命であったからである. |
|
貞治とは直接の関連性はないが, 矢野の著書に見られる事実誤認と思しき他の実例について触れておく. |
| [矢野8] 矢野健太郎『数学者おしゃべり帳』新潮社, 1982, pp.124-125. | |||
| には [矢野2] の「こぼれ話」として数名の学者達の逸話が掲載されている. その中に次のような逸話がある. |
| 若いK教授の話である. K教授は終戦後いち早くアメリカに渡り, アメリカで数々の立派な業績をあげた方であるが, 日本のある大学から要請されて帰国され, その大学の学生を指導することになった. ところがちょうどその時期に, 理学部長の改選が行なわれることになった. K教授のように研究一途の方が理学部長に向いているかどうかについては私には何とも言えないが, それでも選挙となれば, 立派な業績をあげて帰国されたK教授に票が集まりそうな形勢になった. ところが, どこからか,「理学部長に専門馬鹿は困りますね」という妙な言葉がきこえてきた. これを聞いたK教授は, 思わず,「専門馬鹿でない人はただの馬鹿ですか」と反問して動じる色はなかったという. |
|||
| 矢野の著作に見られる各学者の逸話に関しては, 出典が明記されていない. 矢野自身が直接見聞きしたか, あるいは噂ないし伝聞として耳にしたものを, 記憶を頼りに執筆しているように思われる. 上記のK教授が誰を指すものかは [矢野8] を読む限りでは判らないが, これが小平邦彦 (1915-1997) であることは |
| [小平] 小平邦彦『ボクは算数しか出来なかった ―― 私の履歴書』日経サイエンス社, 1987, 全181頁. | |||
| を読めば明らかであろう (pp.152-153). |
| 昭和42年 (1967年) の8月半ばに日本に帰って, 東京大学の数学教室に復帰した. (中略) 翌43年の夏に東大紛争が始まった. (中略) しばしば団交が行われて, 教授達が学生に専門バカと罵倒された. ある日, 紛争に対する理学部の意見をまとめるからめいめい意見を書け, という回覧板が回って来たので, 私は「専門バカでないものは唯のバカである」と書いて出した. そうしたら, この句がそのまま理学部の意見の中に採用されて有名になった. 3年後の昭和46年の11月4日の教授会での選挙で, 私は理学部長に選出された. 怠けものの私はあまり教授会に出席せず, この日もうちにいたら選出されたという電話があった. ギョッとした. アメリカから帰ったばかりで, 日本の習慣もまだよくわからず, 評議員はおろか教室主任もしたことがない私に学部長が務まるとは思えなかったし, 東大に帰るとき雑用はいっさいしなくてよいという約束があったはずであるから, 断ろうと思ったが, 断った先例がないということでついに学部長にさせられてしまった. |
|||
| 上記における矢野および小平の記載事項は互いに齟齬を来している. 何れか一方, または両者共々による記憶違い (事実誤認) があるものと思われる. 小平に関する逸話であるから, 小平自身の記憶違いの可能性は (矢野よりは) 低い. 少なくとも, 小平自身に学部長就任を望んだ気配はない. 周囲の者達が小平の意思に反して学部長に仕立て上げたわけである. であるならば, 矢野の言う「どこからか,「理学部長に専門馬鹿は困りますね」という妙な言葉がきこえてきた. これを聞いたK教授は……」の話は, 事実ではないことになる. 小平が「専門馬鹿でないものは」云々を発したのは教授会においてではないからである. 矢野は, 恐らく, 小平のこの台詞をどこかで聞きかじったものと思われる. 選挙で学部長に選ばれた話も知人から聞き知ったのであろう (当時の矢野は東工大の教授であり, 東大には所属していなかった). この二つを結び付けて話を面白くするために,「どこからか」,「妙な」などという曖昧な表現を付随させてこの逸話を仕立て上げた可能性が高い. 尤も, このような作り話を知人から耳にした矢野が, それを横流しした可能性も拭いきれない. |
 『ボクは算数しか出来なかった』 (日経サイエンス社, 1987) |
| [小平] の原稿が日経新聞に掲載され始めたのは1986年であるから, これを執筆した時点で小平は [矢野8] を読んでいた可能性がある. 無論, 矢野にも同様のことが言える. 但し, 矢野も小平も互いに相手の著書に関しては何も言及していないので, 何れの逸話が事実かに関しては, 私のような部外者には判断しかねる. 戦後「アメリカで数々の立派な業績をあげた」苗字のイニシャルがKの他の理学部長としては, 小平邦彦の前任者久保亮五 (1920-1995) が考えられる. これも矢野の言う「若いK教授」に該当するが, 久保が渡米したのは1963年であり,「終戦後いち早くアメリカに渡」ったとは言えない. 一方, 小平のプリンストン行きは, 次の引用部にもある通り1949年である. 因みに, 戦後に東大の理学部長を務めたイニシャルKの学者は, 他にも, 茅誠司 (1898-1988), 木村健二郎 (1896-1988), 小谷正雄 (1906-1993), 朽津耕三 (1927-2021) などが存在するが, 彼らの経歴を見れば, 矢野の言う「終戦後いち早くアメリカに渡り, アメリカで数々の立派な業績をあげた方」に該当しないことは明白である. [小平] では,「プリンストン行き」の章で, 貞治との関わりが紹介される (p.83). |
| プリンストンの高級研究所の所員には全然義務がなく, 自分の好きな研究をしていればよい, という話を聞いて, (中略) 行けたら, さぞうれしいだろう,
とは思ったが, 怠けものの私はこちらから願書を出す, などということには全く思い至らなかった. 昭和23年の春, 菅原正夫先生から,「高級研究所のワイル教授に君の推薦状を書くように高木貞治先生にお願いしておいたから」という話があった. それから半年ほど経ってワイル教授から, 1949年 (昭和24年)9月から一年間高級研究所に来ないか, という招待状がきた. 早速, 菅原先生と一緒に高木先生のお宅にお礼に行ったら, 高木先生は悠然として「エヘヘ……実は怠けていてまだ何も書いてないんで……」と言われた. なるほど, 大先生というものはこういうふうに悠然としているものか, と感心した. |
|||
| 同様の記事は [追想高木] pp.162-163 にもある (両者の原稿の執筆時期は, ほぼ重なっている). 貞治が小平の推薦状を書かなかったとしても, 何かの折に直接または伝言をもって小平の件をワイル (Hermann Weyl, 1885-1955) に伝えた可能性はある. 仮に貞治がワイルに対して何の働きかけもしなかったとするならば, 純粋に数物理学上の業績をもってプリンストン高等研究所 (Institute for Advanced Study) から招聘された小平の実力は見事というほかはない. [追想高木] では, 上記の逸話に続けて, 学士院賞受賞の際の貞治に関して |
| 昭和32年の春, 高木先生から「学士院賞を貰っていただきたく, ついては論文の別刷を送っていただきたく……」という手紙を戴いた. (中略)
面倒かも知れないが我慢して別刷を送って学士院賞なるものを受賞してほしい, という調子の文面で, 受賞が決ってお目出度うなどということは書いていなかった,
と記憶している. 日本に帰って学士院会員になってみて, 数学の業績に学士院賞を出すには, その業績が賞に値する重要なものであることを第ニ部の多数の会員が納得するように説明しなければならず, それが非常に難しいことを知り, 当時82歳の高木先生が私のために大変な苦労をして下さったことに感謝の念を新たにしている次第である. |
|||
| と回想されている (pp.163). 余談であるが, [小平] (p.129) には後日談が載っている. 貞治から上記の手紙を受け取った小平には, 授賞式に出席せよという通知は来なかったようである. その「通知は東京の留守宅の母の所で止まってしまったらしい. 授賞式には母が代わりに出席したと後で聞いた.」とある. [矢野2] に掲載された数学者達や物理学者達の逸話は, (多少の脚色はあるにせよ) 面白いものが多い. 脚色を疑えば際限がないが, その件は保留にして, 貞治自身の言及が存在する例を紹介しよう. 矢野はまず, ドイツ留学から帰国したての新進気鋭教授であった貞治が集合論の講義で学生に説明したことを紹介する. \(\mathbb{N}\,\)のような可付番 (abzählbar) 集合の濃度を\(\,\mathfrak{a}\), \(\mathbb{R}\,\)のような連続 (continuum) 体の濃度を\(\,\mathfrak{c}\,\)で表せば, \(\mathfrak{a}\!<\!\mathfrak{c}\,\)である. その後, 矢野は次のように続ける. |
| 高木先生は,「濃度\(\,\mathfrak{a}\,\)より大きく, 濃度\(\,\mathfrak{c}\,\)より小さい濃度をもつ無限集合は存在するか, という問題は連続体の問題とよばれるが, この問題はまだ解決されていない」と言ってこの講義をしめくくられた. 先生が教室を出ようとすると「ハイ」と言って手を挙げた学生がいた. 先生が何だねと尋ねると, その学生は「先生がいま言われた連続体の問題解けました」と答えた. 先生が, ほうどんな具合にときき返したところ, その学生は「\(\mathfrak{a}\,\)と\(\,\mathfrak{c}\,\)の間は\(\,\mathfrak{b}\,\)に決っています」と答えたという. ([矢野2], pp.18-19) | |||
| この逸話に関しては, |
| [高木掛谷]『高木貞治 掛谷宗一 兩博士縱橫對談記』/ 考へ方研究社『高數硏究』第5卷第8號 (1941年5月), pp.24-35. | |||
| において貞治自身が言及している. この対談全般に亘る貞治と掛谷の遣り取りは大変に面白いが, それらは割愛して, 濃度の関する部分のみを抜粋しよう. |
| 洒落で面白かつたのは何時か集合論の講義をしてゐた時に, 濃度が\(\,\mathfrak{a}\,\)と\(\,\mathfrak{c}\,\)との間の集合はあるかないか分つて居ないといつて敎室を出たら, 或る學生が黑板の處へ行つて\(\,\mathfrak{a}\,\)と\(\,\mathfrak{c}\,\)との間には\(\,\mathfrak{b}\,\)があるとやつたんだ. (笑聲) この洒落はインターナシヨナルだから記錄にとつておき給へ. (笑聲) 巧い洒落をいつたものだと思つて, 非常に感心した. 保證に半分位判を捺してもいゝんだけれども, 相憎頼みに來ないんだ. (笑聲) それとも誰かに習つて來たのかも判らないね. | |||
| 貞治はこの学生を賞讃して「この洒落はインターナショナル」としているが, 各々の記号が異なる言語の頭文字を採られている (可算濃度を独語で, 連続体濃度をラテン語 (または英語) で表記している) 点が気に掛かる. 慥かに, カントールは "continuum" を用いたが, これはラテン語であって独語 "Kontinuum" ではない. 仮に, 可算濃度の記号にラテン語版 "numerabilis" の頭文字を当てたとしても, この洒落は成立しないし, 可算濃度を\(\,\aleph_0\), 連続体濃度を\(2^{\aleph_0}\,\)または\(\,\aleph_1\,\)で表すこと多い現代にあっては猶更である. その点, 貞治が [體系] において発した「ビ分のことはビ分でせよ」, あるいは, [矢野2] に掲載されているような, 太平洋に棲息する種々の魚類の分布状態に関する統計学者の説明を受けた直後に角谷静夫 (1911-2004) が発した「それはポアソン分布か?」(pp.80-82) の方がセンスが良い. 後者は, 数学者間の会話であれば「インターナショナル」として通用するであろう. 上記の学生による洒落は, 貞治が言うように, 当時の学生達あるいは一部の学者達の間では既に言い古された小噺の類であったかも知れない. |
| [矢野7] ではもう一つ有名な逸話が語られている. |
|
私が在学中の東大数学科の時間割は, 何時から何時までは何と, 1時間きざみで表示されていた. しかし教室から教室への移動などで時間がかかるので,
実際には先生方は, 15分過ぎか20分過ぎに教室へこられた. しかし高木先生は, たとえ先生のお部屋まではきておられても, 必ず30分過ぎに教室へこられて, 30分間講義をして下さった. 私が大学院へ入れてもらって, 少しは先生に心易く口がきけるようになってから私は, 先生にその理由をたずねてみた. すると先生は 「矢野君はアカデミック・コーター (大学の15分) ということを知っているかね」 ときかれた. これは大学の先生はふつう時間より15分は遅れてくる, という意味である. そこで私が聞いたことがありますと申し上げると 「ふつう講義は15分過ぎに始まることになっているのだろう. それにアカデミック・コーターを足すと30分になるよ」というのが先生のお答えであった. なんとも良き時代であったと言わざるを得ない. |
|||
| 大学における貞治の講義が定刻より遅れて開始されることは, 一時的な現象ではなかったらしい. 教え子達達によるこれに関する回想部分のみを [追想高木] から抜粋してみよう ( [ ] 内の数字は, 当人が東京帝大の数学科を卒業した年を表す). |
| 先生はいつも25分過ぎくらいに見えられた. そして内ポケットから小型の手帳を取り出されてから御講義を始められた. (増井真須夫 [1925卒], p.28) | |||
| 始業時間に15分くらい遅れて講義が始まることが多かったのに, 一時間分の内容を越える充実した講義であった. (吉田耕作 [1931卒], p.73) | |||
| 一回の講義時間は短くて, 30分か40分だがその内容は充実していた. (倉石治七郎 [1931], p.79) | |||
| 高木先生の講義は必ず30分遅刻して来られたが, 残りの30分で結構内容豊富のものであった. (小松醇郎 [1932卒], p.87) | |||
| 時間表には午前10時から11時までとなっている講義に, 先生はいつも判で押したようにきっかり10時半に教室に現れ, 先生独特の講義を正味30分で終わり, さっと引き上げて行かれた. (浅野啓三 [1933卒], p.97) | |||
| 先生の講義は実に理路整然としていて話しに繰り返しがなく, 無駄な言葉がなく, 聞いていて胸のすくような思いがした. だからいつも一定時間きまって遅刻されたにもかかわらず, 講義の進み方が速く内容が充実していた. (村勢一郎 [1934卒], p.115) | |||
| 先生の御講義は, 規定一時間のところ, 実質30分, その御来場は風の如く迅速であり, 12時の呼鈴と共に御退場も脱兎の如く俊敏である. (北川敏男 [1934卒], p.121) | |||
| 高木先生の御講義は11時からとあったので, われわれは11時15分までに, 教室へ集って先生をお待ちしていた. ところが, 先生はもうとっくにお部屋まで来ておられるはずなのに, 11時30分までは教室にお見えにならなかった. いつも11時30分になるとはじめて教室へお見えになり, 11時30分に講義をお始めになった. (矢野健太郎 [1934卒], p.128) | |||
| 彼らの回想によれば, 講義時間が規定より短かったというその講義内容に無駄がなかったのみならず, 教室への入退場の仕方にも無駄がなかったようである. この点は哲学者西田幾多郎の講義と対照的であろう. 余談であるが, 下村寅太郎 (1902-1995) は,『「高木貞治先生の生涯」落穂拾い』([追想高木] pp.258-266) において, 貞治と幾多郎の関わりについて詳しく記している. 引き続き, この逸話に関して引用する. |
| 高木先生の講義はいつも11時から12時の時間帯で組まれており, 確か週3回であったと記憶している. (中略) 先生は11時からお待ちしているわれわれの処へ, 約20分ぐらい遅れて (中略) それから約40分ぐらい, 先生は考えながら最も簡明で直裁的でしかも最も一般化された独特の思考過程の講義を展開されてゆかれた (後略) (山内正憲 [1935卒], pp.135-136) | |||
| 教室に11時から12時までのその時間 (ただし先生は20分ぐらいは遅くいらっしたように思うが), 早くから前の方に席を確保して毎度お待ち申し上げたのである. (亀谷俊司 [1936卒], p.139) | |||
| 当時は講義は50分単位であったが, 学生の集中力は30分が限度というのが先生の持論であったらしく, 毎回きっかり11時半に教室へおいでになり, 12時にはピタッとおやめになった. (栗田稔 [1937卒], p.144) | |||
| 高木先生の講義は週4回で, 一回の講義は約30分ほどだったが, ゆったりとした話し方で先を急ぐという感じは一度もなかった. (古屋茂 [1938卒], p.158) | |||
| 時間割のうえでは講義は11時から12時までとなっていたが, 高木先生が数学教室に到着されるのが11時10分頃, それから先生は小使室で悠然とお茶を飲んでおられた. (中略) 講義が始まるのが11時半, 終るのが時間割通り12時きっかりであった. (中略) 講義の内容は先生が当時の岩波講座『数学』に執筆された『解析概論』とほぼ同じであった. 11時半から12時まで正味30分, 週4回で2時間, それで一年間で『解析概論』の終わり (現行本のルベッグ積分は除いて) まで済まされたのだから不思議である. (小平邦彦 [1938卒], pp.161-162) | |||
| 一回30分余りで, 必ず一つのトピックをすまされるので, 講義をきいた後に, 一種の充実感を味わうことができました. (中略) 全く無駄のない講義で, 知らぬ間にどんどん進んで,『解析概論』の膨大な内容を一年間で殆んどカバーされたのは不思議な程でした. (伊藤清 [1938卒], p.166) | |||
| 講義には, 高木さんはおそく来て, 時間の半分位しかやりませんでした. (杉村欣次郎 [1912卒], p.201) | |||
| 先生は11時半頃になると正門の方から大股で坂を下りいきなり教室にはいってこられます. 講義は30分間でしたがどの教授のよりも充実していました. (菅原正夫 [1925卒], p.222) | |||
| 聞くところによると, 先生は夕食に好物のお酒を召上り, 間もなくおやすみになり夜半に起きて明け方まで数学の研究をなさり, またおやすみになるとのこと, 当然朝寝になり大学に来られる時間が遅れ, したがって講義の時間が短くなるということだったらしい. しかし私達にとっては, 講義の時間が短かかったからまだよかったので, 同じことを二度繰り返されず, 要点だけを押えていかれるので, 内容はずいぶん豊富だった. (正田建次郎 [1925卒], p.226) | |||
| 貞治が講義の開始時刻を常に定刻より遅らせた理由は何であったか. 上記の引用箇所には,「学生の集中力は30分が限度というのが先生の持論」(栗田), あるいは (毎晩明け方まで研究していたため)「朝寝になり大学に来られる時間が遅れ」(正田) とあるが, 何れも「らしい」という伝聞または憶測によるものである. 後者の「朝寝」は正鵠を逸しているようである.「先生はもうとっくにお部屋まで来ておられるはずなのに, 11時30分までは教室にお見えにならなかった」(矢野), あるいは「高木先生が数学教室に到着されるのが11時10分頃, それから先生は小使室で悠然とお茶を飲んでおられた」(小平) とある. これに関して, 矢野は, 上掲の [矢野7] と同様の逸話を [追想高木] (pp.128-129) や [矢野2] (p.21) などでも披露している. 話としては面白いが, これが実話なのか矢野の創作なのかは判らない. 実話であるとしても, 真の理由に関しては別問題である. 貞治流のユーモア (矢野が揶揄われた) という可能性も否定できないからである. 少なくとも, この矢野が述べる内容と同一の理由が記載された (他の教え子達による) 著作を私は見かけたことがない. [追想高木] では, 矢野の他に, 浅野が唯一, この理由に関して貞治に尋ねた人物の話題を提供している (p.100). |
| 講義の場合には, 10時頃すでに先生は教授室まで来ておられたのに, 何故か30分の間をおいて開始されるのであった. その理由を, 図らずも,
一年先輩の木下佳寿氏から聞く機会があった. 同氏は卒業式の日に「先生はいつも10時半から講義をされましたが, それはなぜでしょうか」と直接に高木先生に質問された由で,
そのときの答えは次のようであった. 「もともと学生諸君は10時には遅れずに教室に来ておらなければならない. そして30分の間にこの前はどんなことを学んだかを調べ, それを復習して, 続いて聴く講義に対して準備を整えておくべきである. クラインがこのようにやってみてたいへん有効であったといっている.」 |
|||
| 上記引用部において, 講義時間が規定よりも短かかったにも拘らず, その内容は豊富で充実していたという記載が, 複数箇所に見られる. 無駄がなく同じことを繰り返しさない, という記載も散見される. 彼らの卒業年度から見て, 多くの者は, 貞治が類体論の創始者として有名になった後の時代の学生達である. 貞治を畏敬するあまり, その講義に対する盲目的な崇拝もあったであろう. 例えば, 講義中の貞治の声は小さかった, あるいは, 黒板に書かれる文字は薄かった, などの状況に関しても,「高木貞治」を畏敬する教え子達には, 何か深淵なものに思えてくるものらしい. 引き続き, [追想高木] から引用する. |
| 先生が親指と人さし指でチョークを持たれ, 黒板をいたはるかの如くに字を書かれ, 声帯に負担をかけまいとするかの如くに静かな声で講演されたことを思ひ出す (佐藤良一郎 [1916卒], p.17) | |||
| 先生に最初に御免謁したのは大正11年 (1922) の最初の御講義の時であった. 当時の理学部本館の階段教室で, 十数名の新入生は何となく遠慮して, 皆少し後の席に坐っていた. 先生のお名前は入学前より存知あげておったので, 緊張してお待ちしておった. いざ御講義が始まり, ノートを取ろうとしたところが, お声が聞きとれない. 皆呆然としているうちに御講義は終ってしまった. 私にはこれは頭をどやされたようなショックであった. (増井真須夫 [1925卒], p.27) | |||
| 講義は, 我々の方に向って, 笑みを含みながら静かな口調でゆっくりと話される. 同じことは繰り返されないが, 抽象的な事柄でもまるで目前にあるもののようにありありと話されるので誠に心地よく理解することができた. 要所へくると少し声を高められる. よく白墨の先を小さく折ってから黒板へうすく式や図を描かれる. (寺阪英孝 [1928卒], p.42) | |||
| 私が高木先生に始めてお目にかかったのは, 東大数学科に入学を許された昭和3年 (1928) 4月で, この月に先生の「代数学」の講義とその演習に始めて出席した日のことであった.
先生の講義は明晰であることはもちろんであるが, 同じことを繰り返しては言われないことが特徴であった. (中略) ただしお声が大きくはなく, また黒板に書かれるチョークの字も稍々薄い (中略). 高木先生の講義は繰り返しをされないので, いささかの懈怠も許されず, 真の学問修行の座に列しているような喜びがあった. (吉田耕作 [1931卒], pp.72-73) |
|||
| 憧れの高木先生の整数論の講義はユニークだった. (中略) 奇麗な建造物か彫刻でも仰ぎ見るように雄大壮大だった. 講義の後は何回か繰り返し反すうの必要があった. (倉石治七郎 [1931卒], p.79) | |||
| 指先でつまむようにチョークを持って書かれる板書の文字はうすく, 悠然たる話し方ではあったが, 言葉数は少なく声は小さくて, 目をこらし耳をそばだてたものである.
ゆっくりとした調子で講義を進めておられるようにみえたが, 後になって講義のノートを調べると, 意外に内容が豊富で, (中略) 先生の講義は, (中略) 長年繰り返して推敲を重ねられたもので, 実によくまとまっている. いかに多くを盛り込むかではなく, つねに本質的なものを念頭において, 省くべきは省いて, いかに短くするかに本格的に苦心を払われたものである (中略). 定理の証明一つにもそれなりの工夫のあとが感じとられ, エレガントな証明が随所に見出される. 理論の展開は鮮かで分りやすく, 私にとっては芸術品にも似た香り高い魅力的なものであった. (浅野啓三 [1933卒], pp.97-98) |
|||
| 高木先生は真に数学を愛し, 理解し, 純粋に数学の中に没入し, 俗世界に左右されず, かと言って俗世間を蔑視せず, 愛想笑いをせず, 怒りの表情を微塵も出さず, 人の気持を忖度するような面倒なことは一切せず, 三十数分の授業をいつも淡々とひとりごとのように楽しんで語る. (安部道雄 [1933卒], p.107) | |||
| 高木先生の御講義は始まったが, ここでも困ったことがおこった. それは先生のお声がいかにも小さく, また黒板にかかれる字もいかにも小さいことであった. それでも聴き落としたりすることがあっては大変なので, 講義の後では, あちらこちらの参考書を読み, ノートの整理は大変であった. (矢野健太郎 [1934卒], p.129) | |||
| 声はどちらかといえば低い方で, 広い教室の後ろの方に席をとるとききとりにくいこともあった. 黒板の文字や式はやや小さめではあったがていねいにきれいに書かれた. (古屋茂 [1938卒], p.158) | |||
| 高木先生は声も小さく黒板に書かれる字も薄かったので, 後の方の席に坐ったわれわれにはよく聞こえないし見えなかった. (小平邦彦 [1938卒], p.161) | |||
| これらを読む限りでは, 貞治への畏敬の念を強くもつ学生, あるいは学力の優秀な (あるいは学力優秀だと周囲から認められたい) 学生は, 貞治の講義を肯定的に捉える傾向があるように見受けられる. 言い換えれば, 貞治の講義を理解できないこと, あるいは貞治の講義方法を肯定できないこと, その原因を全て自己の学力不足や努力不足に帰する傾向がある (従って, 自ら努力してこれを理解し, これを肯定的に捉えるように努めている) ように思われるのである. その一方, やや距離を置いてこれを客観的に捉える者も存在する. |
| 高木先生は数々の名著をあらわされたが, (中略) 高木先生の書かれた本とその講義について少くとも外見的には非常に隔りがある (中略) 高木先生の御本は理路整然, 懇切叮嚀, 快刀乱麻, 時にはジョークを交えて流麗の筆になるようです. これに対し御講義の方は, 少くとも昭和初頭の頃在学した学生達にとってはかなり難渋な, 更には神韻縹渺として捕らえがたいもののようでした. なぜあのように著書と講義の間に違いがあるのだろうか. 著書は一般の人にも読まれるものだから判り易く明快に書くことが必要で, 講義は大学の数学専攻の学生達だけがきくものだから要点だけを簡単にと配慮されたとも考えられます. 要はこれを聴く学生側にあるというわけで, これをたとえようもない名講義とし, とぎれとぎれの要点から珠玉の思想を汲みとるか否かは学生の腕前という考えです. (恒川実, p.82) |
|||
| 貞治の著書は慥かに「理路整然」であり「明快」と言えよう. 一回につき僅か30分の講義で一つのトピックを纏め, 緩やかに進む通年の講義で『解析概論』の大半を終えることは, やや無理があるように思う. 要点のみの講義であったからこそ, 聴講後, 学生達は他の数学書を調べたりノートを整理しながら復習したりする必要が生じたのであろう. ここに見られる彼らの自己研鑽力は, 現代における一般の大学生のそれとは雲泥の差がある. それを貞治への憧憬に後押しされるながら苦ともせず継続し得たからこそ, 彼らもまた優秀な数学者と成り得たのであろう. |
| 貞治は,『微積の體系といつたようなこと』において,「微分のことは微分で…」のような考え方は, 両足が揃っているのに敢えて片足で歩行するような無益な苦行と断じた. 貞治の著書が明快で理路整然としている最大の理由として, 論理の流れおよび証明の手法が自然であることが挙げられよう.『初等整数論講義』や『解析概論』における独自の工夫を加えた説明あるいは証明は, 読者を感嘆させるものが多い.『高等教育代数学』に掲載された問題に対する解答は, その手法に関して何れも鮮やかで美しく, やはり読者を感嘆させる. そこでは, 問題に解答する際は単に正答を得ればよいわけではない, 常に単純明快を旨とせよ, と学生達に注意を与えたのであった. また, 貞治は, 自身を等身大以上に見せたり過大評価されたりすることを好まず, 数学に対しては厳密な理解を旨とし, 理解不足を決して誤魔化さない謙虚さを兼ね備えていた. このような貞治の学究姿勢ないし教育方針は, 折に触れて教え子達にも伝授されたようである. [追想高木] には次のような回想が記されている. |
| ゼミにおいて, 菅原さんはヘッケの数論の教科書 (1923), 正田さんはフロベニウスとシューアの論文を (中略) 講読され, 問谷さんはシュパイザーの群論の初版 (1922) を講読に用いられた. このゼミは三人の熱意が直かに感ぜられるようなゼミであった. 高木先生は, 温顔を以て静かに講読を聞かれておられたが, 時々「そうは行かぬ」と仰せられた. そうすると講読者はほとんどかならず立往生をされてしまった. まことに鋭い御指摘であった. (増井真須夫 [1925卒], p.28) | |||
| 私達が初期の頃, 何かといえば鉛筆を取って計算などを始めようとする態度をたしなめられた (中略) 書物は "lessen zwischen den Zailen" (行間を読み取れ, 眼光紙背に徹する) とか言われた (寺阪英孝 [1928卒], p.44) |
|||
| 寺阪は, 貞治の言葉として「書物は行間を読み取れ」と記しているが, 寺阪以外の者がこれに関して言及しているのを私は見掛けたことがない. 寺阪は, 上記引用部以外にも, |
| [寺阪] 寺阪英孝『幾何学研究の思い出』/ 寺阪英孝, 南雲道夫, 守屋美賀雄 共著『数学のながれ』上智大学数学教室, 1977, p.6. | |||
| において,「高木先生の本を読む態度としての教訓は, Lesen zwischen den Zerilen (行間を読め) ということであった.」と記している. 但し, これに関して, 貞治自身が『解析概論』の「緒言」に同様の文言を記していることは既に述べた通りである (§4-9). |
| ゼミの第一回目, よくわからない本の内容と悪戦苦闘やっと話し終えた途端, 先生がおっしゃった「ちっとも面白くない」, これにはぎゃふん. 結局要点だけを簡明に言えばよかったのに, 始めから終わりまでだらだらと冗長に話したのがお気に入らなかった次第. あらかじめ一言, 要点だけを簡単に話せばよいのだよと注意されないところが, 先生の面目躍如たるところでしょう. 数学科の学生たる者は, 注意されなくとも自得すべきだという, 一生忘れ得ない御教訓だったようです. (恒川実 [1931卒], p.83) |
|||
| 演習の時間は特にこわい時間であるとともに数学を考究する態度を悟らせるものであった. へまなことをしていると横を向いていた先生が「そんなことそしていてはしようがない」やがて「退れ」と言われる. (小松醇郎 [1932卒], p.87) | |||
| 当時は, 数学抽象化の盛んな時代であった. 高木先生は, よく「看板の塗り替え」などと皮肉を言われたが,「看板も塗り替えている中に, 何かが出て来るかもしれない」と言われもした. (中略) セミナーではたった一回だけ, イデアル論の中で使われていた選択公理の役割が面白くて, ここは熱を入れて報告した. 先生は何か, にやにやされながらそれを聞いておられたが, 最後に一言,「ペダンティックだね」と言われた. 著者に対してか, 報告者に対してか, とにかく私には, この一言は身に沁みてこたえた. (小野勝次 [1933卒], pp.93-94) |
|||
| 先生のよく口にされた言葉で, エッセンシャルとトリヴィアルがいつまでも私の耳に残っている. 先生流にいえば,「数学で何かがよく分ったというのは, 何から何まで, すみからすみまでよく分ったということではなく, 何がエッセンシャルで何がトリヴィアルであるか, その区別がよく分ったということである. エッセンシャルなものを追求し, 重視する, 重要性の認識が本質である.」(浅野啓三 [1933卒], p.98) | |||
| 先生は (中略)「君, ラゲールの全集を読んでみないか」と言われた. 先生のお考えはすぐに分かった. ラゲールの論文は方法が奔放であり着想が面白いということを一年生のとき講義か演習で聞かされていた.
ラゲールは解析を用いて代数の定理を得ているが, これらは純粋に代数的な方法で証明し直せるはずであるから, やってみよというのが先生のお考えであると思った.
(中略) うまくいったのはスツルムの問題に関するいわゆるラゲールの定理だけであった. しかしその代数的証明を求めるということは先生が絶えず気にしておられたものらしく,
私の証明を聞いて下さったとき, 一言「よくやった!」と仰言って下さった. 嬉しかった. なお, その証明をあとで先生の『代数学講義』の改訂版に載せて下さった.
(中略) ある時, (中略) シュタイニッツの定理は証明が面倒であるが如何でしょうかと伺ったところ,「ああいうものは, あるものとして……」とさりげなく仰言った. 軽くいなされたわけである. と同時に私はハッとした, この類の定理は, (中略) その概念の認識に立ってその先を考えるところに意味がある, というのが先生のお考えのように思われて, 私は目を開かれる思いがしたのであった. (中略) 一年生のときの代数学演習の時間に, 誰かが「帰納法で証明します」とやったところ, 終ったあとで「帰納法は素人のやるものだ」と仰言った, これも妙に心に残っている. (村勢一郎 [1937卒], p.117, p.119) |
|||
| 演習のとき, この証明はよくないなどと余計なことをつい口にしたら, 先生から数学の証明にはよしあしの判定基準はないとたしなめられた. 先生のお言葉ながら果たしてそうだろうか.
そこで, 自分が当たったとき, 整数論の演習問題を解くのに, 微積分をつかった証明を板書して引き下がった. 先生は嫌な顔をなさっている. しかし先日のことがあるからお叱りになるわけにも参らぬとお見受けした.
(中略) 高木先生はよく言われた.「何が essential で, 何が trivial か, その区別が大切である.」「いかに怠けるかが大切である.」「自分で機関車にならなければ数学者になれない.」(北川敏男 [1934卒], p.121, p.125) |
|||
| 私達が, 先生の方法と異った解法を外国書などで見出して先生にお話申上げると「そんな方法でやるとコーシー先生が泣くよ」などと言って笑っておられた
(中略) 「学究の徒は, なにがエッセンシャルであり, なにがトリヴィアルであるか, を見極めることが肝腎である」といわれたことがあった . (山内正憲 [1935卒], pp.136-137) |
|||
| 先生はしばしば独特のうまい言いかたで数学の感覚的内容を示唆なさった. (中略) 三角級数のところでファイエ (Fejér) (中略) の定理の証明にうまい計算を示され,「こんなズルイ計算なんかして……」と言われたのである. 賞めっぱなしにはしたくないお気持ちが窺われた. (中略) 大は小を兼ねるという辞書式網羅主義を, 先生は採られなかったように思う. たとえば有限項のテイラー展開で最後の剰余の項はいろいろに表わすことができるのであるが, 私たちは最も標準的なものを一つ知ればよかった. 時間がもっとあればやるというのではなく, あったとしても敢てそれはやらないのである. (中略) 不定形の極限といわれたものについても, 実解析的定理については触れられていない. テイラー展開を知っていれば済むことだからである. (中略) 正項級数の収束・発散の判定条件ではガウスの条件を代表に選ばれた. (中略) 先生の御講義の中でも複素関数の部分は圧巻であった. われわれはほとんど陶酔したといってよい. 私自身も先生の魅了する力の虜になったために解析学の一分野にのめり込んだらしい. (亀谷俊司 [1936卒], pp.141-142) |
|||
| 講義は, 実数の性質として, 上に有界な単調増加列は極限値をもつということを前提として始められました. 厳密にいうといくらでも遡ることになるから, この辺から始めるとおっしゃった様に記憶しています. 私は『新撰算術講義』で実数の厳密な定義をしておられるのを覚えてましたので, この出発のしかたは意外でしたが, 暫らく聞いている中に先生が直観と論理とのバランスを考えて講義を進められるのがよくわかりました. (伊藤清 [1938卒], pp.165-166) | |||
| 先生の示されたお考えの一端, 例えば「若い者は三つのAとGという分類によって専門化されず, 広くモダンな数学を勉強しなければならない」とか「essential と trivial の区別が肝要である」と言うようなことは, われわれ学生仲間の間の標語となっていた. (河田敬義 [1938卒], p.168) | |||
| 先生が黒板に書かれる字は, うすいけれど丁寧に書かれました. (中略) ゼミナールの時, 話がつまらないと窓の方を向いたりしていました. つまらないことを長くは御免だという気があるんでしょう. (三村征雄 [1928卒], pp.205-206) |
|||
| 貞治は, 自身がその講義や著書で見せた「独自の工夫を加えたエレガントな手法」を, ゼミにおいて学生達にも (口にしないまでも) 求めていたのであろう. 意に沿わない発表をする学生達には,「面白くない」あるいは「退れ」と言ったり「横」あるいは「窓の方」を向いたりしつつ, それを伝えたのであった. 「エッセンシャル」と「トリヴィアル」に関しても多くの教え子達を感化したようである. これは, 前出の西田幾多郎にも見られる学究姿勢であった.「本物の哲学者には必ず独自な考え方がある. 書物を読むというのは, その骨をつかむことだ.」あるいは「骨がわかってしまえば, 何も最後のページまで読む必要はない」というものである (高山岩男『西田哲学とは何か』燈影舎, 1988). |
| [追想高木] pp.286-294 には, 貞治の著作目録が掲載されている. まず,「欧米論文」27篇については, 本稿の §3 における [高木1] から [高木26], および『帝国学士院紀事』に発表された『オイラー方陣についてのノート』 |
| [高木27] T.Takagi "Note on Eulerean Squares" Proc. Imp. Acad. Japan, Vol.22, 1946, pp.113-116. | |||
| が全てであり,「著書」に関しては, 本稿の §3 で採り上げた『あーべる方程式ニツキテ』から §6 に掲げた著作までのものが全てである. 随想録や回想録などの小篇に関しては, 本稿各所で引用したもの以外にも数篇が存在する. ここでは, その中の一つ, |
| 高木貞治『訓練上數學の價値 附數學的論理學』/ 吉江琢兒, 高木貞治, 田邊元『一般敎養としての數學について』岩波書店, 1936, pp.37-70. | |||
| を採り上げておこう. 岩波茂雄 (1881-1946) による「はしがき」によれば, これは, 1935年12月26日から28日に開催された, 文部省主催による高等学校の文科における「数学教授改善」を「目的」とする, 高等学校の教員向けの講習会における「講義録」であるという. ここにおける貞治の講演を見ると, |