| 評論・随筆・記録 |
| 管弦楽《名曲50選》 1994 | 管弦楽《続・名曲50選》 2004 |
| 西田幾多郎と京都学派 2001 | スティーヴ・ライヒの音楽 2024 |
| フェルマーの最終定理と未解決問題 2003 |
| 高木貞治と類体論 |
| 2025年 執筆 |
| 目次 |
| 貞治は, その生涯の大半を数学者 (研究者) および大学教授 (教育者) として過ごした. 教育者としての貞治に関しては次節に回すことにして,
本節では, その両者の立場に基いて創出された著書について見ていくことにしよう. 貞治の最初の著書は, 大学院生時代 (洋行直前) に著した |
| 高木貞治『新撰算術』帝國百科全書第六編, 博文館, 1898, 全297頁. | |||
| である. 貞治はこのとき23歳であった. |
 『新選算術』(博文館, 1898) |
| 序文を見ると, |
| 「アリスメチック」ノ語ニハ二樣ノ意義アリ. (中略) 前者ヲ算術ト稱シ, 後者ヲ整數論と云フ (中略) 本書説ク所ハ, 此所謂算術ニ外ナラズ. (中略) 此書ノ眼目トスル所ハ, 讀者ヲシテ數ノ精確ナル觀念ヲ得セシメントスルニアリ. 抑々數學ニ於ケル數の觀念カ十分明晰ニ説明セラレ, 最嚴密ナル意味ニオ於テ論理的ニ完全ノモノナレルハ, メテ輓近ノ事に屬ス. (中略) 此智識は高等數學ヲ修ムルノ階梯トシテ, 欠クヘカラサル者ナリ. |
|||
| とある. 要するに, 小学校時代から慣れ親しんだ「数」を一度精密に見直し, 高等数学を学ぶ確固たる基礎固めを目的としている. 対象とする読者は明記されていないが, 恐らく, 初等教育に携わる教員か学部生または大学院生であろう. 全6章49節から成る書籍で, その内訳は |
| 第一章 整数 (整数の四則演算, 冪乗, 合同式) 第二章 整数の性質 (公約数と公倍数, 素因数分解, \(\varphi(m)\,\)の性質, フェルマーの小定理) 第三章 分数 (分数と小数の四則演算, 加比の理, 循環小数と循環節) 第四章 冪根 (冪乗と冪根, 有理数の限界, 開平算) 第五章 無理数 (数列または有理数の切断による無理数の定義, 無理数の大小と四則演算) 第六章 量及其測定 (量の相等と大小関係, 量の連続性, 量の測定, 長さ・面積・体積) 結 論 負数, 虚数および実数, 代数学の基本定理 |
|||
| となっている. 丁寧な解説であるが, 緻密な議論を積み重ねるため, 全てを精密に読むには根気がいる. 決して読みやすくはないが, 数学の根柢を形作る数の大系が過不足なく展開されている著作である. 『新撰算術』は「帝國百科全書」なるシリーズの中の一冊に収められた. 本文の後に掲載された宣伝文句を見ると,「全部壱百卷, 紙數壱册壱三百廿頁, 毎月壱回發行」とあり, 発刊の主旨として「専門學述の普及を促して已まず, 本書は乃ち此急需に應じて起りたる者にして, 會智識の指導を以て任ずる者, 獨り僻郷師に乏しき者の爲のみとせんや, 大都大中學に在るの士も, 亦本書に俟つ所必ず多大なる者あらん」と書かれている. この読者に対する向学心啓発欲に満ちた出版社 (博文館) の意気込みと, 狭窄的な営利中心主義に傾く現今の出版業界とを想うとき, 甚だしき隔世の感を否めない. |
| その「帝國百科全書」には貞治の2冊目の著書 |
| 高木貞治『新撰代數學』帝國百科全書第十七編, 博文館, 1898, 全296頁. | |||
| も収録された. これも貞治が23歳のときの著作である. |
 『新選代数学』(博文館, 1898) |
| これは前作『新撰算術』の続編とも言うべき著作であり, この頃 (即ち貞治が『あーべる方程式ニツキテ』を書いた頃) に繙いたであろう [Serret1], [Serret2], [Weber1] の内容と重複するものである. 全9章64節から成る書籍で, 内訳は |
| 第一章 序論 (演算, 実数, 数の大小関係, 虚数とその幾何学的表示) 第二章 有理関数 (四則演算, 二項定理, 剰余の定理, 最大公約, 有理関数, 導関数とテイラー展開) 第三章 方程式の根 (複根, 整関数の連続性, 根の存在, ラグランジュの補間法) 第四章 整関数の有理分解 (関数の可約と既約, ガウスの補題, アイゼンシュタインの定理) 第五章 多変数関数 (多変数関数の同次性, 項の数, 分解, 展開) 第六章 対称式論 (冪和, 対称式の基本定理, 交代式, 判別式, 終結式, チルンハウス変換) 第七章 行列式 (行列式の性質, 小行列式, 行列式の積, 連立方程式, 補間法) 第八章 二次形式論 (二次形式の行列式, 二次形式の平方和への変形) 第九章 三次および四次方程式 (カルダノの解法, 四次方程式の解法, チルンハウス変換, ラグランジュの解法) |
|||
| となっている. 『新撰代數學』は, 前作の『新撰算術』と異なり, 序文に該当するものがない. そのため, 執筆目的は不明であるが, 貞治の恩師である藤澤利喜太郎が後年に発表した報告書 |
| [藤澤] R.Fujisawa "Summary Report on the Teaching of Mathematics in Japan" 文部省, 1912. | |||
| によれば (Chap.VII "The teaching of mathematics in higher middle schools"),
東京高等師範学校 (1886年設立) および広島高等師範学校 (1902年設立) の第2学年において『新撰代數學』が教科書として用いられたという. ところで,『新撰代數學』の序論の第一節には |
| 代數學ニ於ケル硏究ノ主眼トナルヘキモノハ, 數ノ値即其大小ニ關係スル者ニアラスシテ, 寧ロ數ノ算法ニ關係スルモノナリ. 算法トハ畢竟一定ノ順序ニ與ヘラレタル二個ノ數ヨリシテ,
新ニ第三ノ數ヲ定ムル方法ニ外ナラズ. 代數學ニ於テ用ヰラルヽ算法は所謂加減乘除ノ四則ニ限レリ. 吾輩ハ此處ニ此四則算法ヲ支配スル根原的ノ法則ヲ略叙シ, 讀者ノ記臆ヲ新ニシ, 以テ新硏究ノ地ヲ成サント欲ス. |
|||
| とある. ここでも, 数学の根柢となる数の演算構造を厳密に構築しようとする貞治の姿勢が如実に窺えよう. その後, 代数学全般に亘り綿密なる議論が展開された後, 第九章の最終節において, 貞治の代数学に対する思想が再び明確に表現される. |
| 方程式ノ代數解法ハ代數學ニ於テ最重要ナル問題ニシテ, 代數學ハ其實方程式ノ硏究ニ外ナラスト謂フモ過言ニアラサルナリ. 四次以下ノ方程式ノ解法ハ十五六世紀の交旣ニ以太利ノ學者間ニ知ラレタル所ナレトモ, 其解法ハ個々其趣ヲ殊ニセリ. ラグランジュハ此等ノ解法ノ根柢ニ一貫セル系統ノ潜在セルヲ看破シタル後, 更ニ此一貫ノ經路ヲ尋ネテ五次以上ノ方程式ノ解法ヲ索メタレドモ其効ヲ奏セザリキ, 今日ニ於テハ, 五次以上の一般ノ方程式ノ代數的解法ハ絕對的ニ不可能ノ事ナルコト旣ニ證明セラレ方程式ノ硏究ハ別に新進路ヲ採ルに至レリ. 此最モ趣味饒キ硏究塲裡ニ入ルニ及バズシテ茲ニ讀者ニ辭セサルヲ得サルハ吾輩ノ最も憾トスル所ナリ. 讀者若シ更ニ進テ現今代數學ノ眞相ヲ究メント欲セハ請フ去テウェーバー敎授ノ有名ナル敎科書 (H. Weber, Lehrbuch der Algebra) を繙ケ. |
|||
| 洋行直前,『あーべる方程式ニツキテ』を完成させた貞治が最も関心を抱いていた代数方程式論の最先端を, この著作において一般読者に示唆したのであった. 『新撰代數學』は, 日本人著者による最初の本格的な代数学の専門書と言えよう. |
| 洋行を経て帰朝した後, 1904年に東京帝大教授に就任した貞治は, 同年, |
| 高木貞治『新式算術講義』博文館, 1904, 全436頁. | |||
| を上梓した. このとき貞治は29歳であった. 当然のことながら, 前二作の表紙にある「理学士」なる記載が, ここでは「理学博士」に書き替わっている. |
 『新式算術講義』(博文館, 1904) |
 『新式算術講義』(ちくま学芸文庫, 2008) |
| この著作の執筆目的は「緒言」に明記されている. |
| 算術敎師が算術の知識を求むる範圍, 其敎ふる兒童の敎科用書と同一程度の者に限らるゝこと, 極めて危殆なりと謂ふべし, 確實なる知識の缺乏を補ふに, 敎授法の經驗を以てせんとするは,「無き袖を振はん」とするなり. 又数學を專攻せんとする學生にありても, 目下の狀態に於ては, 其算術の知識は幼時普通敎育によりて得たる所に限られ, 漸く進んで稍々高等なる数學諸分科の修業に入るに當りても, 數學の根源に關せる問題を囘顧して, 精密に之を復習するの遑なきが如し. 斯の如くなれば其知識は堅牢なる地盤を缺くが故に, 學ぶ所愈々進むに随ひ, 知る所愈々不確実となる. |
|||
| 小学校以来, 充分に理解したと思っていた事柄が実はそうでなかったという例は少なくない. 例えば, 中学生や高校生であっても, 小学校の範囲である「\(a\!\div\!b\,\)は\(\,a\!\times\!(1/b)\,\)に等しい」ことの説明ができないという事例は (少なくとも私の携わる教育現場では) 多々見られる. 中学校におけるユークリッド幾何, 高等学校における三角関数や微積分などが, (その出立点において) 厳密性に欠ける前提や素朴な直観に基いて構成されていることも (教員側にとっては) 周知の事実である. 貞治は, このような事柄に関して, 再度顧みて精密に理解せよと注意を喚起したのである. 『新式算術講義』は全11章から成り, 内容は |
| 第一章 自然数の起源 (順序数, 基数, 自然数の公理) 第ニ章 四則算法 (可換律, 結合律, 分配律, 除法の原理, 冪乗, 2数の最高位の係数および桁数の比較) 第三章 負数, 四則算法の再審 (数学的帰納法の原理, 負数の演算法則, 絶対値) 第四章 整除に関する整数の性質 (合同式, 不定方程式, 算術の基本定理, 素数の無数性) 第五章 分数 (既約分数, 有理数の稠密性, 比例式, 有理数の四則演算) 第六章 分数に関する整数論的の研究 (部分分数分解, \(\varphi(n)\,\)の性質, フェルマーの小定理) 第七章 四則算法と形式上不易 (数が従うべき一般的な演算法則, 除法の例外) 第八章 量の連続性及無理数の起源 (量の比較, 有理区域に属する量, ユークリッドの比例論) 第九章 無理数 (上限と下限, 有理数の稠密性, 有理数の切断, 無理数の四則演算) 第十章 極限及連続的算法 (極限, 集積点の存在, 基本列, 連続的算法の定義と拡張) 第十一章 冪及対数 (冪乗の存在と極限, 有理数の指数, 無理数の指数, 開平算) |
|||
| である. 藤澤がその著書『算術條目及敎授法』(1895) ,『算術敎科書』(大日本圖書, 1896) において, 算術から量の概念を除外しようとしたのに対し, 貞治は積極的に量およびその連続性を扱っている. また, 統計学にも造詣が深かった藤澤は, 上掲書において, 歩合算や利息算や年金算などを採り入れ, その関係から級数や対数をも扱っていた. それを意識したのであろうか, 貞治も『新式算術講義』において, 極限や対数など解析的な内容を「算術」に含めているのである. 些細なことであるが, 貞治は『新式算術講義』第六章において, 現今ではオイラーの関数 "Euler's totient function" として知られる\(\,\varphi(n)\,\)を「ガウスの函数」(p.174) あるいは「ガウスは\(\,\varphi(n)\,\)なる記號を用ゐたり」(p.197) と述べている. 前作『新撰算術』の第ニ章 (pp.89-100) では\(\,\varphi(m)\,\)に関して固有名詞は登場しないが,『初等整数論講義』(後述) の第一章 (p.41) では「Euler の函数\(\,\varphi(n)\,\)」として紹介されている. 貞治が如何なる理由でガウスの名を挙げたのか, 出典が気になるところである. 数学の専門書でありながら縦書きを余儀なくされる和製数学書のスタイルには, 貞治も辟易したことであろう. 巻末の「附録」には, |
| 「フート, ノート」といふもの邦文の書に入り難し. 本文の各處に添ふべき重なる引用及參照書目を取りまとめて, 卷末に附するに當り, 印刷の進行中に心つきたる本文の修正追補ニ三を收む. | |||
| とある. 15ページに亘るこの (当時としては珍しい) 「脚注」から, 興味深い記述を少し抜粋してみよう. |
| 「代數的の數」(中略) につきて注意すべき一條あり. 古風の數學書又は通俗數學書 (特に或種の初等敎科書) 等に於て此語を負數又は所謂不盡冪根などの義に用ゐたる者なきを保せず. 然れども斯の如きは當今の數學社會一般に用ゐらるゝ用語例を違犯せる者なり. (中略) | |||
| Dの右及左に如何なる點をとるとも, 其中間には必點 (Dより外の) あり. Dの直に右, 直の左の點なる者なし. 連續の定義はデヾキンドの名著, 連續及無理数 (Dedekind, Stetigkeit und Irrationale Zahlen, 1872) に載す. これ必讀の書なり. (中略) | |||
| 此書に於てはデヾキンドの連續の法則を採りて, アキシオマチツクの方法に準じ以て數の觀念を說明せり. 但本邦の一般讀書界の程度を顧慮して, 形式的に論理の最嚴密なるを期せざりき. | |||
| 上記の諸書に於ける叙述の調子槪して全く量の觀念を離れ, 最抽象的に卒然として無理數の定義を立し數と量との關係は讀者の推考發明に一任せり. 而し讀者の多數は其自ら補充すべき所の者を自ら補充することをせずして, 之を說明の不明に歸せしめんとするの傾向を有するが如し. | |||
| 此種の叙述は論理上間然する所なしと雖, 一般讀者の讀書力を信用すること多きに過ぎたりと謂ふべし. 予の舊著「新撰算術」に於ても紙幅節儉の爲此種の叙述法を採りたり. (中略) | |||
| 上掲の引用部では割愛したが, 貞治はこの「脚注」において, \(4k\!+\!1\,\)あるいは\(\,6k\!+\!1\,\)なる形の素数が無数に存在することを巧妙に証明している. また, 無理数の定義についても, 無限小数を拡張するヴァイエルシュトラスの手法を簡明に説明している (本文では基本列数によるカントール (Georg Cantor, 1845-1918) の方法や有理数の切断によるデデキントの方法も紹介されている). なお, この「脚注」の後には,「學用語對譯」として, |
| ・エラトステネスの篩 sieve of Eratosthenes, crible d'Eratosthène. ・集積點 Häufungsstelle, Verdichtungspunkt, point limit. ・不定方程式 indeterminate equation, unbestimmte Gleichung. |
|||
| など, 和語と英語ないし独語の対訳が付されている. これも, 読者の便宜を図ってのことであるが, これを掲載することは, 当時の和製数学書としては初めてに近い試みであったと言えよう. |
| 『新式算術講義』を著した貞治は, その後, 東京帝国大学理科大学教授 (理学博士) としての執筆義務を負ったか, あるいは執筆依頼を受けたかなどの経緯により, 多くの教科書を執筆した. |
| [追想高木] 河田敬義編『追想 髙木貞治先生』高木貞治先生生誕百年記念会, 1986. | |||
| の巻末にある「著作目録」を見ると,「著あるいは編著」のリスト |
| 『普通教育算術教科書』,『普通教育代数教科書』(1904) 『女子教育算術教科書』,『女子教育代数教科書』,『女子教育幾何教科書』(1907) 『廣算術教科書』(1909) 『師範教育数学教科書 [算術・代数]』(1910) 『師範教育数学教科書 [平面幾何・立体幾何]』,『新式算術教科書』,『新式代数教科書』,『新式幾何教科書 [平面・立体]』,『新式三角法教科書』(1911) |
|||
| が掲載されている. 出版社は何れも開成館である. 「普通教育」や「新式」は旧制中学校および高等学校で,「女子教育」は高等女学校で,「師範教育」は高等師範学校で採用されていたものと思われる. このリストの中の教科書から下記の二冊を繙いてみよう. 因みに, これら教科書類は全て横書きで書かれている. まず,『普通敎育代數敎科書』を見ると, 冒頭の「例言」即ち序文には, |
| 普通敎育に於ける代數學敎授の目的は, 生徒をして文字を使用して卑近なる問題を自由に解釋する能力を取得せしむるを以て足れりとすべし. 是故に嚴密なる抽象的の論證は此書の最も忌避する所にして, 常に算術を囘顧して應用上の問題を明透集密に處理することは, 其の最も力を致せる所なり. |
|||
| とある. 前作の『新式算術講義』が教師用として理論構築の厳密性を重視したものであったのに対し, 本作は普通教育の生徒用として厳密性よりも実用的運用力の向上を企図したというのである. 貞治の教育に対する姿勢の一斑が窺えるであろう. この教科書は, 上下二冊に分冊されている. 上巻の内容は現今の中学校から高等学校初学年にかけての内容 (整式の四則演算 (ただし除法は単項式に限る), 因数分解, (連立を含む) 一次方程式) であり, 下巻は現今の中学校高学年から高等学校全般にかけての内容 (二次方程式, 分数式, 冪根, 対数, 級数, 順列と組合せ, 二項定理) になっている. 何れの巻末にも補習問題がちょうど150題ずつ付されている. 例えば, 上巻の問題は |
| 6. 四時四十八分ニハ時計ノ短針ハ長針ヨリモ幾分畫ダケ後ニアルカ. 叉\(\,m\,\)時\(\,n\,\)分には如何. | |||
| 55. 或試驗ノ受驗者二百六十人ニテ, 受驗者全體ノ平均點數64, 及第者ノ平均點數67, 落第者ノ平均点數57ナリ. 及第者及ビ落第者各〃幾人ナルカ. | |||
| 116. 次ノ方程式ヲ解ケ. \((b\!-\!c)(x\!-\!a)\!+\!(c\!-\!a)(x\!-\!b)\!+\!(a\!-\!b)(x\!-\!c)\!=\!d\) | |||
| 149. 七圓七十錢ノ買ヒ物ヲナシ十圓紙幣ヲ出シテつり錢ヲ取リタルニ, 二十錢, 十錢, 五錢ノ三種ノ貨幣合セテ二十四枚ヲ得タリ. 此中, 白銅貨ノ數ハ二十錢銀貨ノ數ノ二倍ナリシト云フ. つり錢ノ勘定ニ誤リナカリシカ. | |||
| などであり (各問の冒頭の数字は問題番号を表す), 下巻の問題は |
| 184. 次ノ方程式ヲ解ケ. \(1\!-\!x\!=\!\sqrt{1\!-\!x\sqrt{4\!-\!7x^2\!\:}\!\:}\) | |||
| 224. \(\alpha,\beta\,\)ガ二次方程式\(\,x^2\!+\!px\!+\!q\!=\!0\,\)ノ二ツノ根ナルトキ, \(\displaystyle{\frac{\,p\alpha\!+\!2q\,}{2\beta\!+\!p}}\,\)ヲ簡單ニセヨ. | |||
| 262. 兵數ノ比\(\,A\!:\!B\,\)ナル東西兩軍ガ交戰シタルニ, 戰死者ノ數の比ハ\(\,a\!\!\::\!\:\!b\), 生還者ノ數ノ比ハ\(\,c\!\!\::\!\:\!d\,\)ナリシト云フ. 兩軍ニ於ケル戰死者ト生還者トノ比各〃幾許ナルカ. | |||
| 294. \(x\,\)ヲ含メル整式ノ五乘冪ヲ計算シテ, 之ヲ\(\,x\,\)の降冪ニ排列セルニ, 其始ノ二項ハ\(\,x^{10}\!\!-\!5x^9\,\)ニシテ, \(x^8\,\)の項ハナシ. 第四項以下ヲ書キ添ヘヨ. | |||
| などである. 現今の教科書に見られるような (解法パターンの定まった) 紋切型の問題の羅列ではなく, 一問一問に対して丹念に取り組みたくなるような独自性の強い問題が数多く含まれている. 尤も,「普通教育」とは言え, 当時の中学校は義務教育ではなく経済的にも学力的にも選ばれた学生のみが進学し得た場所であったことは考慮されねばならない. |
| 次に,『廣算術教科書』を見てみよう. これも上下二冊に分冊されている. 上巻の内容は |
| 第一篇 緒論 第ニ篇 四則 (加法, 減法, 乘法, 除法, 四則の應用) 第三篇 諸等算 (長さ, 面積, 体積, 重さ, 時間, 貨幣などの単位, 単位の変更と演算) 第四篇 整数ノ性質 (約数, 倍数, 倍数判定, 素数, 素因数分解, 最小公倍数, 最大公約数) 第五篇 分数 (分数の四則演算, 循環小数) |
|||
| であり,下巻の内容は |
| 第六篇 比及ビ比例 (比例, 複比, 連比) 第七篇 歩合及ビ利息 (合計高, 残高, 単利法, 複利法, 租税, 保険, 公債, 株式, 手形, 年金) 第八篇 開法 (平方根, 開平算, 無理数, 不盡根数, 立方根) 第九篇 求積 (矩形, 平行四邊形, 梯形, 三角形, 直角三角形, 円, 直方体, 柱体, 円柱, 角錐, 円錐, 球) 第十篇 省略算 (近似値, 省略寄セ算, 省略引キ算, 省略掛ケ算, 省略割リ算, 省略開平) |
|||
| である. 何れも各項目ごとに例題や問題が豊富に掲載され, 巻末には略解が付されている. 序文が存在しないため, 執筆意図や対象読者は不明であるが, 商業系の内容を含む実用性を追求した教科書と言えよう. 上巻第三篇には, |
| 佛國ぱりーノ萬國めーとる同名度量衡局ハめーとる法の物指及ビ分銅ノ原器ヲ保管ス. 物指ノ原器ハ白金製ノ棒ニシテ, 攝氏零度ノ溫度ニ於ケル此棒ノ兩端ノ間ノ長サヲめーとるトイヒ,
之ヲ長サノ單位トス. 一めーとるハ地球子午線ノ長サノ約四千萬分ノ一ニ等シ. 分銅ノ原器モ亦白金ニテ作リ, 其目方ハ大約一めーとるノ十分ノ一ヲ一邊トセル立方體ト同ジキ體積ノ蒸餾水ノ攝氏四度ニ於ケル目方ニ等シ. 此目方 (一きろぐらむ) ノ千分ノ一ヲぐらむト名ヅケ, 之ヲ目方ノ基本單位トス. |
|||
| のように度量衡の万国共通の単位の定め方の記載や (pp.149-150), |
| 地球ガ太陽ヲ一週スル時間ハ三百六十五日五時四十八分四十六秒 (365.2422日) ナリ. サレバ一年ヲ365日トスルトキハ, 此端下0.2422日ガ積リテ,
四年ニハ0.9688日即チ約一日トナル. 故ニ四年目毎ニ366日ノ閏年ヲ置ク. サレド, 是ニテハ四年毎ニ 1-0.9688=0.0312日ダケ多過グルガ故ニ, 四百年ノ後ニハ約三日ノ差ヲ生ズ. ヨリテ四百年ノ中ニ三度閏年ヲ省クナリ. (カヤウニスルトキハ四百年中ニ0.12日ノ狂ヒヲ生ズレドモ, 是ガ積リテ一日ノ狂ヒニナルハ約四千年ノ後ナルベシ). |
|||
| のような閏年の定め方の記載 (p.171) も見られる. 下巻にも, 租税 (所得税, 営業税, 関税, 府県税, 市町村税) や株式 (配當歩合, 利廻りなど) に関する詳しい説明があり, 読んでいて大変に面白い. |
| 『新式算術講義』を上梓したのと同年の1904年に, 貞治は |
| 高木貞治『髙等敎育代數學』東京開成館, 1904, 全404頁. | |||
| を上梓した.『新式算術講義』で解明された初等的な算術から, 本格的な代数学へと一歩進んだ内容をもつ講義式の数学書である. |
 『高等教育代数学』(東京開成館, 1904) |
| 序文によれば, |
| 此書ハ (中略) 普通敎育ノ程度以上ニ於テ, 初等代數學ノ一部分ヲ說カントスルモノナリ. 然レドモ取材ノ範圍ハ初等敎育ニ所謂代數學ノ埒外ニ逸スルコトナク,
唯少シク論證ヲ嚴密ニシ, 問題ノ解釋ヲ詳細ニセル點ニ於テ, 稍是ニ凌駕セルニ過ギズ. 純正代數學ノ智識ト趣味トノ本邦數學界ニ普及センコトハ, 編者ノ切望スル所ナリ. |
|||
| とある. その後の文脈から判断すれば, 前掲の「教科書」類における「代数」と西欧数学界にて称される "Algebra" とはレヴェルおよび内容の異なるものであり, この書籍はその階梯的役割を担うと述べているのである. 内容は, |
| 第一篇 緒論 (整式と四則, 展開と因數分解, 対稱式と交代式, 齊次式, 分數式, 複素數) 第ニ篇 一次方程式 (聯立一次方程式を含む) 第三篇 二次方程式 (聯立二次方程式を含む) 第四篇 不等式 (不等式の原則と解法, 絕對不等式, \(n\,\)次不等式, 分數不等式, 極大極小) 第五篇 代數式の數値の變動 (一次函數, 二次函數, 分數函數, 方程式の根の變動) |
|||
| であり, 一見すると前掲「教科書」類と差異がないように見える. しかし, この書籍を繙くと, ここには随所に貞治の数学思想が鏤められ, 扱われる題材も学生への有意義な示唆に富んだものが多いことに気づかされるのである. 例えば, 交代式の項目において, 辞書式順序で\[\,ab\!+\!ac\!+\!bc,\:\:\:\:\:(a\!-\!b)(a\!-\!c)(b\!-\!c)\,\]と表記すべきところを\[\,bc\!+\!ca\!+\!ab,\:\:\:\:\:(b\!-\!c)(c\!-\!a)(a\!-\!b)\,\]と表記することには「特別ノ理由アリ」とする (pp.32-33). 即ち, \(bc,\,ca,\,ab\,\)以外の文字 (\(b\!-\!c,\,c\!-\!a,\,a\!-\!b\,\)以外の文字) が順次\(\,a,\,b,\,c\,\)となるように配置するというのである. また, 上式の各々において\(\,ac,\,a\!-\!c\,\)ではなく\(\,ca,\,c\!-\!a\,\)と表記することに関して, |
| コハ所謂循環ノ順序ニシテ次の圖ヲ參照シテ其意義ヲ覺ルベシ. | |||
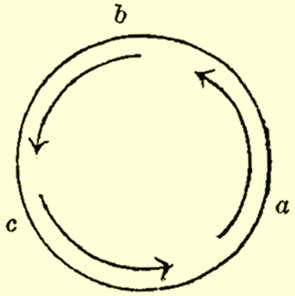 |
|||
| とした上で,\[a^2(b\!-\!c)\!+\!b^2(c\!-\!a)\!+\!c^2(a\!-\!b)\,\]を表記するに際して, 第ニ項のみ負号を用いて\[a^2(b\!-\!c)\!-\!b^2(a\!-\!c)\!+\!c^2(a\!-\!b)\,\]と表記することは「錯雜セル幼稚ナル記法」と断じている. 貞治は続けて次のように述べる. |
| 此處ニ言ヘル如キコトハ, 決シテ拘泥スベキコトニアラズ, 叉一見甚タ些細ナルニ似タリト雖, カヽル些細ナル點ニツキテモ意ヲ用ヰルヘキ餘地アルコトハ, 篤學ノ士ノ注意ヲ要スル所ナルヘキカ. 是ニ於テ吾人ハ我讀者ト共ニ次ノ宣言ヲナスベシ: 代數學ニ於テ數ヲ表ハスニハ, 如何ナル文字ヲモ用ヰ得ヘキ自由アリ. 宜シク此自由ヲ善用シテ, 記法ノ成ルヘク便利ニ, 成ルベク明透ナルヲ勉ムヘキナリ. |
|||
| 数を表す文字に関する貞治の思想は, 後述する『初等整数論講義』(p.277) においても現れる. また, 分数式の通分と見れば直ちに最小公倍数 (式) を持ち出す学生への戒めを |
| 最小公分母ニ通分スヘシトイフ普通ノ規則ノ如キハ, 唯凡テノ場合ニ通用スヘキ一種ノ簡便ナル計算ノ方法ニ過ギズ. (中略) 必スシモ其勞ヲ償フニ足ルノ利益ヲ與フルモノニ非ズ. 理論ノ根本ニ屬スル事ト, 計算ノ枝葉ニ關スル事トハ截然區別セラルベキナリ. | |||
| のように与え, 実例として |
| 例一. \(\displaystyle{\frac{1}{\!\:x\!+\!a\!\:}\!+\!\frac{1}{\!\:x\!+\!3a\!\:} \!+\!\frac{1}{\!\:x\!+\!5a\!\:}\!+\!\frac{1}{\!\:x\!+\!7a\!\:}}\) |
|||
| 例ニ. \(\displaystyle{\frac{b}{\!\:a(a\!+\!b)\!\:}\!+ \!\frac{c}{\!\:(a\!+\!b)(a\!+\!b\!+\!c)\!\:}\!+\!\frac{d} {\!\:(a\!+\!b\!+\!c)(a\!+\!b\!+\!c\!+\!d)\!\:}}\) |
|||
| 例三. \(\displaystyle{\frac{\!\:x\!-\!1\!\:}{x\!+\!1}\!-\!\frac{\!\:x\!-\!2\!\:}{x\!+\!2} \!-\!\frac{\!\:x\!-\!3\!\:}{x\!+\!3}\!+\!\frac{\!\:x\!-\!4\!\:}{x\!+\!4}}\) |
|||
| を簡約させる問題を掲げている (pp.37-39). 貞治が与えた解法は, 一切の無駄がなく鮮やかで美しい. これらの問題は, 20世紀半ば以降の大学入試問題にたびたび登場するようになる. 恐らく, 貞治の時代の教科書や数学書を出典とするものであろう. その後, 貞治が「をぃらーノ公式」と命名する |
| \(E(0)\!=\!E(1)\!=\!0,\:E(2)\!=\!1,\:E(3)\!=\!a\!+\!b+\!c\). 但し, \(\displaystyle{E(k)=\frac{a^k}{\!\:(a\!-\!b)(a\!-\!c)\!\:}\!+ \!\frac{b^k}{\!\:(b\!-\!c)(b\!-\!a)\!\:}\!+\!\frac{c^k}{\!\:(c\!-\!a)(c\!-\!b)\!\:}}\). |
|||
| が紹介される (p.39). 後述する『代数学講義』においては, より一般化された形で "Eulerの公式" として紹介されるものである (p.65). 以下, 興味深い応用例が種々示されるのであるが, この部分は, 他書には見られない貴重な資料と言えよう. 貞治自身, この「オイラーの公式」に少なからず魅了されたのであろう, 巻末の練習問題にも, この公式に纏わる応用問題が複数掲げられている (pp.363-364). また, 分数式における分母の有理化の項において, |
| \[1\!-\!\sqrt{\!\:1\!-\!\sqrt{x\,}},\:\:\sqrt{\!A\!+\!\sqrt{\!B\!+\!C\sqrt{\!\!\:R\,}}}\]等ヲ組織的ニ論センコトハ, 根ガ平方根ノミニ限レル場合ニ於テモ, 仍ホ高等代數學ノ領域ニ屬セル者トナサヾルベカラズ. | |||
| と注意を与えている (p.51).『新式代數敎科書 續卷』(開成館, 1916) の巻末に掲載されている問題 (p.127) |
| 73. 次ノ根數ノ分母ヲ有理化セヨ. (1)\(\,\displaystyle{\frac{\sqrt[3]{6\!\:}}{\!\:\sqrt[3]{3\!\:}\!-\!\sqrt[3]{2\!\:}}}\:\: \) (2)\(\,\displaystyle{\frac{1}{\!\:1\!+\!\sqrt[3]{2\!\:}\!+\!\sqrt[3]{4\!\:}}}\) |
|||
| などと併せ, これらの問題がガロア理論に支配されることを示唆しているのである. さて,『髙等敎育代數學』における方程式および不等式の項目では, 現今の教科書や参考書ではまず扱われないような多岐に亘る問題や解法が紹介され, 読者を惹きつけて飽きさせない魅力に富んでいる. 例えば, 最も単純な一元一次方程式の解法の解説用として, |
| 例一. \(\displaystyle{\frac{x\!+\!1}{2}\!+\!\frac{2x\!-\!1}{3}\!-\!\frac{3x\!-\!2}{4} =\frac{2(5x\!-\!4)}{6}\!-\!\frac{7x\!+\!6}{12}\!+\!3x\!-\!1}\) |
|||
| 例ニ. \(\displaystyle{\frac{a^2(b\!+\!c\!-\!x)}{(a\!-\!b)(a\!-\!c)} \!+\!\frac{b^2(c\!+\!a\!-\!x)}{(b\!-\!c)(b\!-\!a)} \!+\!\frac{c^2(a\!+\!b\!-\!z)}{(c\!-\!a)(c\!-\!b)}=x\!-\!(a\!+\!b\!+\!c)}\) |
|||
| の2題が掲げられ, その一般的解法が示される. その後「一元一次方程式ノ一般ノ解法ハ上ノ如シ. サレド特別ノ工夫ニヨリテ, 解法ヲ短縮シ得ベキ場合多々之アリ.」と述べて |
| 例一. \(8(x\!+\!1)\!-\!3(x\!+\!1)=16\!+\!x\) | |||
|
例ニ. \(\displaystyle{\frac{x\!-\!3a}{4}\!+\!\frac{x\!-\!4a}{5}=\frac{x\!-\!2a}{3} \!+\!\frac{x\!-\!5a}{2}\!-\!\frac{41}{60}a}\) |
|||
| 例三. 五個ノ相連續セル整數ノ和40ニ等シ. 此等ノ數ヲ求メヨ. | |||
| 例四. \((x\!-\!a)^3\!+\!(x\!-\!b)^3\!+\!(x\!-\!c)^3=3(x\!-\!a)(x\!-\!b)(x\!-\!c)\) | |||
| の4題が掲げられ, その解説において貞治流の (やや技巧的な) 鮮やかで美しい解法が開陳されるのである. 単に正答を得ればよいのではない, 解法は単純明快を旨とせよと, 学生に注意を与えているわけである. また,「逆數方程式」(と貞治が称するところの相反方程式) が解説された後, その「應用トシテ最重要ナルハ,1ノ冪根ヲ求ムル方程式ナリ」として, 1の\(\,n\,\)乗根 (\(n\!=\!3,6,12,4,8,5\)) に関して懇切丁寧に解説される (pp.188-195). 少しでも多くの学生を「ガロア理論」ないし「アーベル方程式」の魅力へと早く近づけたいという貞治の想いが垣間見える. 不等式の最後の項目にある「極大極小」は, 微分を用いない (絶対不等式あるいは実数条件のみに依拠する) 最大値最小値の問題が扱われ, 第五篇「代數式ノ數値の變動」では, 方程式不等式の幾何学的解法および関数の最大値最小値 (関数のグラフによる) が扱われる. 後半の「方程式の根の變動」では, 二次方程式の三項のうち一つまたは二つの係数が変動する場合の根の変動について解説され, 特に各係数が特定の変数の一次式となる場合の根の動向は現今の教科書や受験参考書には見られない珍しい話題と言えよう. 因みに, この書籍には巻末に「索引」が掲載されている. これも (先述した「學用語對譯」と同様に) 読者の便宜を図ってのことであるが, これを掲載することは, 当時の和製数学書としては初めてに近い試みであった. |
| 前掲の教科書類は, その後の教育法の改正や時代の趨勢に則って種々の改訂版が出版された. 帝国大学教授として講義を続ける中で執筆されたのが, |
| 高木貞治『代數學講義』共立社, 1930, 全477頁. | |||
| 高木貞治『初等整數論講義』共立社, 1931, 全496頁. | |||
| 高木貞治『解析概論 微分積分法及初等関數論』岩波書店, 1938, 全600頁. | |||
| であった. それぞれ, 貞治が, 55歳, 56歳, 63歳のときの著作である. これらの書籍は, 数学書としては異例のロングセラーであり, 今現在に至るまで頻繁に増刷され続けている. 特に『解析概論』は, (私は数学科出身ではないが, 数学科の友人たちの話では)「数学科の学生の必読書」と言われていたという. ただし, よく売れる書物がその読者達によって精読されているかとなると, 話は別である. 購入しただけで満足したり, 読み始めても途中で挫折したり, という声も少なくない. 私自身にとって,『初等整数論講義』は (本稿の冒頭でも述べたように)「フェルマーの最終定理」との関連性から学生時代に愛読した書籍であり, 他の二冊についても (これまで複数回に亘って) 読み返している. とは言え, 私がこれらの書籍を誤解なく真に理解しているかどうかは疑わしい.『ジャン・クリストフ』や『罪と罰』のような古典文学作品においても, 再読した際に, 初読の際の誤解や, より広角的な視点に気づかされることがある. 内容が深ければ深いほど, 読み返すたびに新たな発見があるものである. 貞治の著作に関しても, 古典文学作品を再読するのと同等の感慨が得られることは事実である. このようなものを「名著」あるいは「古典」と言うのであろう. 以下, これらについても簡単に概略を記しておこう. 『代數學講義』は1948年に [改訂版] が出版され, その後, 貞治の没後 (1961年)に [改訂新版] が出版された. 以下, 引用の際は「改訂新版」から抜粋することにする. |
 『代数学講義 改訂新版』(共立出版, 1965) |
| 「序言」を見ると, |
| 本書は著者がかつて東京大学で初級生のためにした一般向きの代数学講義に基づいて, それに多少の布桁を加えたものである. この講義の目的は, 僅少なる時間に於て,
迅速に代数学の基本概念を解説するにあった. 従って本書の目標とする所も, 代数学の大観であって, 系統的なる全書ではない. (中略) 成るべく多趣多様に代数的方法を紹介することを主眼とするのである. |
|||
| とある. 実際, この著作には一冊の数学書としては贅沢に過ぎるほどの豊富な題材が含まれている. 第1章「複素数」では, その四則, 幾何学的表示, 一次有理関数, 等角写像が扱われる. これは, 次章以降で必要となる基礎事項である. 貞治は, 章末において複素数史を簡単に解説している. |
| Gauss は1799年にその学士論文で代数学の基本定理の証明を発表した後, 整数論の問題に複素数を適用して偉大な成功をもたらし, 次いで
Cauchy は函数論を複素変数の上に築いて, 18世紀の微積分法にまつわった多くの疑問に光明を与え, Abel および Jacobi の楕円函数の発見を可能にする素地を作った.
また射影幾何学の発達は, 幾何学においても, 虚数的原素を導入することの避くべからざることを示した. (中略) 19世紀の中頃に至って, 虚数が一般数学界において承認された後に\(\,1,i\:\)を原素とする二次元の複素数の範囲を更に拡張して多次元の複素数を数学に導入することが問題となった. Hamilton の四元法 (quaternions) や, Grassmann の広延論 (Ausdehnungslehre) がその最初の試みで (後略) |
|||
| このように述べた後, 貞治は四則を保存する数の範囲は複素数の範囲を超越し得ないことを簡潔に説明している. 第2章「方程式論の基本定理」では, 多項式の四則と連続性, 代数学の基本定理と根の連続性, 有理関数が解説された後, エルミート-ビーラーの定理, ガウスの定理, ラゲルの定理が掲げられる. これらの定理は, 貞治自身が「美しい定理」と表現するものである (p.66). |
| 定理2.9 (Hermite) 方程式\(\,f(z)\!=\!0\,\)の根の虚数部の符号が全部同一であるとき, 係数の実部と虚部とを分けて\(\,f(z)\!=\!U(z)\!+\!iV(z)\,\)とすれば, \(U(z)\!=\!0\,\)も\(\,V(z)\!=\!0\,\)も実根のみをもって, かつ\(\,U(z)\,\)の根と\(\,V(z)\,\)の根とは互いに隔離する. |
|||
| 定理2.11 (Gauss) \(f(z)\!=\!0\,\)の根の全部を含む凸多角形は\(\,f^{\prime}(z)\!=\!0\,\)の根の全部を含む. |
|||
| 定理2.12 (Laguerre) (1) 方程式\(\,f(x)\!=\!0\,\)のすべての根を含む円を\(\,C\,\)とし, \(\xi\,\)を\(\,C\,\)の外に取れば, \(P(\xi,x)\!=\!0\,\)の根はすべて円\(\,C\,\)の内にある. (2) \(\xi\,\)が円\(\,C\,\)の周上にあっても同様であるが, 特に\(\,f(x)\!=\!0\,\)の根がことごとく\(\,C\,\)の周上にあるとき, \(\xi\,\)も\(\,C\,\)の周上に取るならば, \(P(\xi,x)\!=\!0\,\)の根もことごとく\(\,C\,\)の周上にある. (3) この場合に, \(P(\xi,x)\!=\!0\,\)の根と\(\,\xi\,\)とは\(\,C\,\)の周上において\(\,f(x)\!=\!0\,\)の根を隔離する. |
|||
| 応用する場面が実用上少なくなったからであろうか, これらの定理が現今の代数学書で採り上げられることはほとんどない. その意味ではもはや数学史上の「骨董品」の部類と言えよう. しかし, この著作の魅力はこのような美術品が多数展示されている点にある. 定理のみならず, 著書全般に亘って随所に鏤められた「問題」も, 演習用 (実用的) というよりは寧ろ鑑賞用とでも言うべき, 味わい深いものが多い. 第3章「スツルムの定理」においては, 方程式の根の個数とその近似を計算する. 前者に関しては, フーリエ の定理, デカルトの符号律, (与えられた正定数より大なる根の個数に関する) ラゲルの定理が採り上げられ, 後者に関しては, ボルツァーノの定理およびロルの定理から平均値の定理を導出した上で, 解析的手法によりニュートンの方法とホーナーの方法が扱われるのである. 第4章「多項式の整除」, 第5章「対称式, 置換」, 第6章「三次および四次方程式」の内容は, その多くが『新撰代数学』と重複する. ここでは, ラグランジュの分解式の由来が新規に追加されている (p.174-176). 第7章「不可能の証明」では,「有理区域」(と貞治が称するところの代数体) の解説から始まり, アーベルによる (ガロア理論によらない) 原始的な方法を踏襲して, 五次以上の方程式の代数的解法の非存在性が示される. 応用として, 角の三等分の不可能性および正\(\,n\,\)角形の作図可能性が採り上げられている. 第8章「行列式」および第9章「二次形式」は, 全体のおよそ3分の1の頁数を占めている. この書籍の中心部分と言えよう. 前者においては, 連立方程式の原始的解法を導入部とし, 行列式の性質やクラーメルの公式, ラプラス展開, 小行列式に関するシルベスターの定理などが紹介される. 後者においては, 行列式を応用した二次形式論が展開される. 標準化やシルベスターの慣性法則, エルミート形式などであり, この箇所においても『新撰代数学』との重複が数多く認められる. 第10章「終結式 スツルムの問題と二次形式」では, 二次形式論を応用して, 方程式\(\,f\!=\!0,g\!=\!0\,\)の終結式から\(\,f,g\,\)の最大公約数の次数を得る手法を導出し, それをシュトゥルムの問題に適用する. 後半部の解説はやや精密さに欠けるが, この章の内容はこの著作の集大成として大変に面白い. 余談ながら, 貞治の著書内における二項係数の表記の変遷について触れておく.『新撰代数学』(p.40) では\[{}_n\mathrm{C}_{\mu}\!=\!\displaystyle{\frac{\prod(n)}{\prod{\!\!\:\mu}\prod(n\!-\!\mu)}}\,\]と表記され,『普通教育代数教科書』(p.405) では\[\,{}_n\mathrm{C}_r\!=\!\displaystyle{\frac{|\!\underline{\:n}} {|\!\underline{\:r}\:|\!\underline{\:n\!-\!r}}}\,\](但し,\(\,|\!\underline{\:\:\:}\,\)は階乗を表す) と表記されていた二項係数は, 最終的に『代数学講義』(p.40) において\[\,\displaystyle{\binom{n}{k}\!=\! \frac{n(n\!-\!1)(n\!-\!2)\cdots(n\!-\!k\!+\!1)}{k\!\:!}}\,\]のように書き換えられた. その理由は「\({}_m\mathrm{C}_k\,\)などとしるせば, 肝心の\(\,n\,\)や\(\,k\,\)が目立たない」というのである. 私はこの最後の表記を好む者であるが, 現今の教科書類は\(\,{}_n\mathrm{C}_k\,\)なる表記で統一されているため, 残念ながら学校現場では使えない. |
| 『代数学講義』の「姉妹篇」として執筆されたのが『初等整數論講義』である. これも貞治の没後 (1971年) に改訂版 (第2版) が出版されている. 以下の引用は全て第2版による. |
 『初等整数論講義 第2版』(共立出版, 1971) |
| 「初等整数論」なる書名をもつ数学書は, これまでに多数出版されている. とは言え, 何をもって「初等」とするかは著者ごとに多種多様であり, 明確な定義は存在しない. 貞治自身は, 初等整数論と題する第1章に関して,「序言」において, |
| 有理整数のみを考察の範囲として進行することが不適当であると思われる所に到達して, そこを一段落とした (後略) | |||
| と述べている.「序言」では, これに続けて, 第2章以下の内容に関する簡単な説明がある. |
| 第2章連分数論は (中略) 整数的近似法 (Diophantische Approximation) の一斑を紹介する. (後略) 第3章では連分数論の応用として二元二次不定方程式を論ずる. ニ元二次不定方程式の解法は十八世紀数学の精華で, 貴重なる古典と言わねばなるまい. (後略) 第4章及び第5章に於ては二次の数体を例に取って代数的整数論の端緒を述べて, イデヤル論の概念を紹介する. (後略) 別に附録の一章を置いて, 二次体論の高等なる部分にも論及し, 且つ二次体のイデヤルの類数の計算及び算術級数中の素数に関する Dirichlet の定理の函数論的証明法を概説する. |
|||
| 『代数学講義』が広範囲に亘る代数分野を概観するものであったのに対し,『初等整数論講義』はその一部である「代数的整数論」延いては「類体論」を目的とする方面に内容を限定するものであった. 本稿の冒頭に引用した黒田成勝の「序」においても,「著者の主なる意図は, 本書を通じて, 読者が代数的整数論に到達するための正統的な道を示すことにある」と明記されている. 貞治が若い時分から「数」が内包する構造に拘り, 数論に興味関心を抱いて主要な研究対象としてきたことは, これまで見てきたことから明白であろう.「序文」の後半において, 貞治は次のように述べる. |
| 整数論の方法は繊細である, 小心である, その理想は玲瓏にして些の陰翳をも留めざる所にある. 代数学でも, 函数論でも, 叉は幾何学でも, 整数論的の試練を経て始めて精妙の境地に入るのである. Gauss が整数論を数学中の数学と観じたる理由がここにある. | |||
| ここに提示されたガウスの言葉は, 恐らく「数学は科学の女王, 算術は数学の女王」"Die Mathematik ist die Königin der Wissenschaften, und die Arithmetik ist die Königin der Mathematik" を指すものであろう. 生前のガウスと親交のあった地質学者ザルトリウス (Sartorius von Waltershausen, 1809-1876) がガウスの没後すぐに出版した評伝『記憶の中のガウス』 |
| [Sartorius] Sartorius "Gauss zum Gedächtniss" S. Hirzel, 1856, 全108頁. | |||
| の79頁に掲載された文言である.「算術」"Arithmetik" は, ガウスの『整数論研究』 |
| [Gauss D.A.] C.F.Gauss "Disquisitiones Arithmeticae" In commiss. apud Gerh. Fleischer, jun., 1801, 全668頁. | |||
 ガウス『整数論研究』(1801) |
| に見られる通り,「整数論」と同義である. 第1章「初等整数論」は, 除法の原理, 素因数分解, 一次不定方程式と合同式, 原始根と指数, 平方剰余の相互法則など, 整数論の基本事項が次々と簡明に解説され, 読者を一気に惹き込む豊富な内容をもつ. 中でも章末にある円周等分多項式と1の冪根から正17角形の作図可能性に至る解説において, 結果の意外性と手法の鮮やかさは初学者を感嘆させるであろう. 第2章「連分数」では, 実数や複素数の連分数展開, 連分数による一次形式論 (ミンコフスキの定理), モジュラル変形による複素数の対等, 無理数の近似と格子点との美しい調和関係が開陳される. 学生時代の私は, 連分数論を応用して方程式の近似解を得る手法や, モジュラー群の基本領域がもつ神秘的な構造に特に魅了されたのであった. 第3章「二元二次不定方程式」では, 二次無理数の対等と連分数展開, 二次無理数の自己変形定理とペル方程式, 二次不定方程式の解法が解説される. 章末に現れる貞治の数学史観 (pp.239-240) は, 特に読者の興味を引くであろう. |
| Gauss の「整数論」では克明に無理数を忌避して, 二次形式を専用しているけれども, それは一種の韜晦であって, 頭の中では\(\,\omega\,\)によって構成した理論を発表するのみ\(\,f\,\)を籍りたかの観がある.
特に\(\,\omega\,\)が虚数 (\(D\!<\!0\)) の場合に, このカムフラージュが最も周到であったのは, 当時の数学界の虚数に対する蒙昧な態度を考慮して,
Gauss のいわゆる頑迷者流の誤解を予防するに至当な戒心であったかと推察される. 「整数論」の後三十年を経て Gauss の複素整数論 (1832) が発表された. (後略) |
|||
| 上記における「整数論」および「複素整数論」とは, 上掲の [Gauss D.A.] および |
| [Gauss1] C.F.Gauss "Theoria residuorum biquadraticorum, Commentatio secunda" Soc. Regiae Sci. Gött., 1832, pp.89-148. | |||
| である. [Gauss1] では, ガウスの整数環が提示され, 四次剰余の相互法則が (証明なしで) 紹介されている. ガウスの研究レヴェルが当時の数学界一般の理解度を遥かに凌駕していたことはよく知られていよう. 彼らの能力を考慮したガウスは, レヴェルを下げて敢えて迂遠なる方法で理論を組み立て直さなければならなかったのである. 貞治は, その当時の事情を次のように続けて記す. |
| 現代の整数論は Fermat (1601-1665) 以来徐々に成育しつつあったのであるが, 十八世紀に至って, 特に Euler (1707-1783),
Lagrange (1736-1813) の努力によって, 二元二次の不定方程式の解法が成就する程度にまで発達して, 数学の一分科を構成するのに十分な域に達したのである.
Legendre (1752-1833) の「整数の理論の試作」(Essai sur la théorie des nombres, 1798) は十八世紀の終りにおける整数論の概括的展観であって, その書名が「整数論」という語の濫觴である. 当時の数学界から仰視されていたこの Essai は未だ平方剰余の相互法則を確定することもできず, また二次不定方程式を解き得ても, その理論が完成されてあるとはいい難い程度のものであった. |
|||
| ルジャンドル (Adrien-Marie Legendre, 1752-1833) の "Essai" 即ち |
| [Legendre] A.Legendre "Essai sur la théorie des nombres" Duprat, 1798, 全471頁. | |||
| の「序文」において, ルジャンドルは, 自身の業績として, 二次無理数と循環連分数の対等性, 四平方定理, 算術級数中の素数に関する定理の一般的方法,
の3つを挙げた. 彼は, この最後の業績を「最も注目すべきもの」"Le plus remarquable" と自負したのであったが,
実際にはその一部, 即ち『初等整数論講義』(p.56) にある「\(mt\!+\!1\,\)の形の素数は無限に存在する」を示したに過ぎなかった. 完全な証明がディリクレ (前出, §2-3) によるものであったことは, 現在では周知の事実である. とは言え, フェルマーやオイラーの業績を初めとする整数論関連の諸結果を微に入り細に亘って解説している点に鑑みれば,「当時の数学界から仰視されていた」のも頷けるであろう. 特に, 巻末に掲げられた (二次形式, ペル方程式, 平方剰余関連の)「数表」は, 30頁以上にも及ぶ労作である! ところが, その労作 [Legendre] の運命はその後どうなったか. 貞治は次のように述べて第3章を終える. |
| そのような世界へ卒然として投げ出されたのが24歳の青年 Gauss (1777-1855) の Disquisitiones (1801)
である. その第四編において初めて相互法則の確定的の証明が提供され, かつその重大性が明示された. またその第五編, 二次形式論の前半において,
二次不定方程式の統一的の理論が構築されている. (中略) Disquisitiones の出現とともに, Essai は三年の寿命をもって急転直下, 数学史料に化してしまったのである. 数学史上の奇観といわねばならない. |
|||
| [Gauss D.A.] が出版された1801年当時, ガウスは24歳, ルジャンドルは49歳であった. ルジャンドルにしてみれば若輩者のガウスには苦々しい想いをさせられたことであろう. この辺りに端を発する二人の確執 (それは一方的にルジャンドル側の問題であったが) については, 後に『近世数学史談』に詳しく紹介されることになる. 第4章「二次体\(\,K(i),\,K(\sqrt{-3\,})\,\)の整数」では, ガウスの整数環, \(x^2\!+y^2\!=a\,\)の解が説明され, 応用としてフェルマーの問題 (\(n\!=\!4,3\)) が解決される. 第4章を敷衍した一般論が展開される第5章「二次体の整数論」は, この著作における中心主題である. 二次体とその整数環, イデアル論の基本定理までが解説される. その後, イデアルの類別, 既約類の個数や特定のイデアルを法とするフェルマーの定理などが示され, ペル方程式や二元二次方程式に応用される. 定理5.18「二次体の素イデアルは三種に分かれる」(pp.292-294) や「与えられたノルムを有するイデアル」(pp.325-326) は, 二次体のイデアルにおける肝要部分である. ここには複数の例や問題が付されており, 貞治の読者に対する細かな配慮が読者の理解度を大いに高める役割を担っていると言えよう. 第5章の内容は『代数的整数論』前半部にある諸事項を二次体に適用したものであり, 両書を対比して読めば, 双方の理解を助けることになるであろう. 余談であるが, (『髙等教育代数学』に現れたような) 数を表す文字に関する貞治の思想は, ここでも顔を出す. p.277の脚注を見ると, |
| イデアルを表わすにはドイツ文字を用いるのが慣例であるが, 本書では便宜上イタリックの大文字を代表する. 筆者はイデヤル論を世界的に普及せしめるために, ドイツ文字専用の慣例をやめて欲しいと思う. ただし二次体論はこれでよいが, 高等整数論ではさしつかえが生ずるから別の考慮を要する. | |||
| と記されている. 最後の一文は1931年の初版 (p.327) には見られないから, 1933年に岩波数学講座『代数的整数論』を執筆した際に気づいた点を, その後の増刷版において付加したものと思われる. ところで,『初等整数論講義』の巻末に付された「附録」は, 第5章に匹敵する注目すべき項目である. 代数的整数論への階梯として, まずイデアルの類別について広義と狭義が区別され, ノルム剰余およびイデアルの属する種に関して解説される. 続いて, 平方剰余の相互法則が二次体のイデアル論を用いて証明される. その単純明快ぶりは読者を感嘆させるであろう. さらに, イデアル類の類数と算術級数中の素数の定理の証明 (ディリクレの業績) の要点が解説される. 前者は, \(K(\sqrt{m\,})\,\)のイデアル\(\,J\,\)によるデデキントのゼータ関数 |
| \(\displaystyle{\zeta_{{}_{K}}\!\:(s)=\sum_{}^{J}\frac{1}{\!\:\mathrm{N}(J)^{{}^{s}}\!\:}}\) |
| を, \(K(\sqrt{m\,})\,\)における素イデアル\(\,P\,\)を用いて |
| \(\displaystyle{\zeta_{{}_{K}}\!\:(s)= \prod_{}^{P}\frac{1}{\!\:1\!-\!\mathrm{N}(P)^{{}^{-\!\:s}}\!\:}}\) |
| のように無限乗積展開したものを, 素イデアル三種を指標\(\,\chi(p)\,\)(p.295) で置き換えて |
| \(\displaystyle{L_{\!\!\:{}_{K}}\!\:(s)=\prod_{}^{p}\frac{1} {\!\:1\!-\!\chi(p)\,p^{{}^{-\!\:s}}\!\:}=\sum_{n\!\:=\!\:1}^{\infty} \!\frac{\!\:\chi(n)}{n^s}}\) |
| なる別表記にした上で, 極限\(\,s\!\to\!1\,\)をとり, 狭義のイデアル類数\(\,h_{\kappa}\,\)を無限級数の和\(\,\displaystyle{\sum_{n\!\:=\!\:1}^{\infty}\!\frac{\!\:\chi(n)\!\:}{n}}\,\)として求めるものである. 後者は, \(\mathrm{mod}.\!\!\:k\,\)に関する指標\(\,\chi(n)\,\)による\(L\,\)関数 |
| \(\displaystyle{L\!\:(s,\chi)=\sum_{n\!\:=\!\:1}^{\infty}\!\frac{\!\:\chi(n)\!\:}{n^s} =\prod_{}^{p}\frac{1}{\!\:1\!-\!\chi(p)\,p^{{}^{-\!\:s}}\!\:}\:\:(s\!>\!1)}\) |
| を三種の素イデアル (p.292) ごとに\(\,L_{1},L_{2},L_{3}\,\)とおいて |
| \(\displaystyle{\lim_{s\!\:\to1}\,(s\!-\!1)L_1(s)=\frac{\!\:\varphi(k)}{k},\: \lim L_2(s)\!=\!L_2(1)\,(\not=\!0),\:\:\lim L_3(s)\!=\!L_3(1)\,(\not=\!0)}\) |
| を示した後, 全ての\(\,\chi\,\)に関する\(\,\log L\!\:(s,\chi)\,\)の和 |
| \(\displaystyle{\sum^{\chi}\log L\!\:(s,\chi)= \varphi(k){\sum}^{\,\prime}\!\frac{1}{\!\:p^s}\!+\!S}\,\) \((s\!\geq\!1\,\)のとき\(\,|S|\!<\!\varphi(k),\:\:p\!\equiv\!1\:(\mathrm{mod}.\!\!\:k))\) |
| を考え, 極限\(\,s\!\to\!1\,\)をとった上で\(\,p\!\equiv\!m\,(\mathrm{mod}.\!\!\:k)\,\)なる有理素数\(\,p\,\)の存在を示すというものである. |
|
何れも厳密に理解することは容易ではないが, 貞治による解説は極めて平易であり, 読者を納得させるものになっている. 最後に, 上述の証明に用いられたガウスの和 |
| \(\displaystyle{\sum^{r}\chi(r)\,\mathrm{exp}\left(\frac{2\pi i}{|\!\:d\!\:|\!\:}nr\right) =\chi(n)\sqrt{\!\!\:d\,}}\) |
| の証明が与えられる. これは,「Gauss が数年苦心の後ようやく解決することを得たといっている」(p.392) 方法であり, 甚だ技巧的であるが, 貞治の述べる通り「含蓄の多い」ものである. その末尾において, 貞治は |
| 二次体と1の巾根との間に密接な関係のあることが感ぜられるであろう. 有理整数に関する二次の問題が二次体の問題として取り扱われるときに透明なる解釈が可能で
(中略) 二次体の整数論もさらに一段の高所から見おろすときに, 初めてその全景をほしいままに展望することができるのである. その展望台は, すなわち1の巾根から生ずる数体
(Abel 体) の理論 (現代的の「円理」!) である. われわれは明媚なる風景に魅惑せられて, いつか予定の目標を超えて, 思わず深入りをしたが, このあたりでひとまず馬を返さねばなるまい. |
|||
| という, 読者を代数的整数論への入口へ導く文言を文学的な味のある表現で全体を締め括っている. 内容の明快さや深さも然ることながら, 随所に見られる貞治独特の文学的な表現は,『初等整数論講義』を「名著」たらしめている根幹の一つと言ってよい. |
| [百年史上] (p.253) によれば, 藤澤利喜太郎が定年退官した翌年の1922年当時, 東京帝大数学科における必修科目の講座を受け持っていたのは, |
| ・第一講座 [関数論] 竹内端三 ・第二講座 [微分積分学] 坂井英太郎 ・第三講座 [代数学] 高木貞治 ・第四講座 [微分方程式論] 吉江琢兒 ・応用数学講座 [幾何学] 中川銓吉 |
|||
| であった. 貞治は20年以上もの間, 一貫して代数学を講じていたわけである. 学生時代より藤澤利喜太郎に代数学の必要性を吹き込まれ, アーベル方程式を勧められて類体論まで創設した貞治は, 自他ともに認める代数学の専門家であり, 当然これは貞治が担当すべき講座であった. ところが, [百年史下] (pp.4-5) によれば, |
| 昭和時代に入ると学生や大学院生の数もふえ, とくに高木, 吉江の指導の指導の下に若い層の研究は一段と活気を呈することになる. (中略) 講義の担当者は, 微分積分学は坂井から1932年に高木に移り, (中略) 代数学の講義は1932年に高木から末綱に移った. |
|||
| という (pp.4-5). 末綱恕一 (1898-1970) は, 正田建次郎 (1902-1977), 菅原正夫 (1902-1970), 黒田成勝 (前出, §1-1), 三村征雄 (1904-1984), 彌永昌吉 (前出, §3-5) などの「貞治から直接指導を受けた数学者」のうちの最初期の人物であり, 1924年から東京帝大の助教授に就任していた. 帝国大学令が公布された1919年以降「必修, 選択, 参考科目の区別が付けられ, 卒業の要件として, 必修科目の履修の他に, 選択科目を2科目以上修得しなければならないこととなった」という. 末綱は, 選択科目「解析的整数論」も担当していたようである ([百年史上] p.231, p.253). 代数学の大家であったとは言え, 貞治による類体論は (先述したように) ゼータ関数や\(\,L\,\)関数など解析関係の道具を駆使している. これが可能であったのは, 貞治自身が若い時分に専門分野を早急に狭めてしまわず, 縦横無尽に種々の分野の数学を咀嚼吸収してきたからこそであった. 貞治が担当した「微分積分学」について, 彌永昌吉は |
| [彌永10] 彌永昌吉『河田君のこと』/『柔らかい頭と強い腕 河田敬義追想集』私家版, 1994, pp.13-14. | |||
| において |
| 1935年の4月に始まった学年では, 高木先生は, 前期の微分積分学の講義を受け持たれた. 微分積分学というのが, 当時の学科の名前であったが, 内容は先生の『解析概論』と大体同じであった. (先生は, 長い間代数学や整数論の講義をしておられたが, 坂井英太郎先生が定年退職された1932年から前期の微分積分学を受け持たれた. それを岩波講座に書かれたのがもとになって『解析概論』ができたのである. もっとも最後のルベーグ積分の章だけは, 増訂版で追加された). | |||
| と述べている. この講義に関しては, 後年, 多くの学者達によってその印象が語られることになる (詳細は最終節 (§6-3) で紹介する). 僅か半年間の講義で, しかも与えられた時間よりも短時間で講義を済ませてしまったようであるが, 過不足のない充実した講義であったという. 実際,『解析概論』は, 貞治自身が監修した岩波講座 "数学" 全30巻 (1932-1935) の中の8分冊分を, 後に単行本化したものである ([百年史下] p.137). 1932年から1935年に亘って刊行された岩波講座には, 貞治のほか, 小松醇郎 (1909-1993), 藤原松三郎 (1881-1946), 窪田忠彦 (1885-1952) 達が編集委員に加わっていたようである. ) 森茂雄『書物は手元に』(前出書 [追想高木], p.68) によれば, |
| 偶々グルサの Cours d'analyse の全訳の原稿を岩波書店の編集部に持ち込んだ人がいて, その上梓の是非について先生方のご意見を伺ってくれと頼まれていましたので, その趣きを席上で披露しました. そのとき, 先生は,「最早, 我々の手で適切な解析の書物を作り上げる時に来ているのではないか」という意味のことを述べられ, 同席していた岩波茂雄氏から,「先生が, この気概をお持ちなのに, お若い方が学ばなければ」と批判されたこともありました. | |||
| とある. 編集会議でこのように述べた貞治は,『解析概論』を自ら執筆したのであった. 「微分積分法及初等関數論」なる副題が付された初版以降, ルベーグ積分を含めた増訂版 (1943), 改訂第三版 (1961年), 改訂第三版 [軽装版] (1983) を経て, 現在刊行されているものは [定本] 版 (2010) である. 私が学生時代に所蔵していたのは [軽装版] であるが, 以下の引用は全て, 現在の私が所蔵している [改訂第三版] (1961) からの抜粋である. |
 『解析概論 改訂第三版』(岩波書店, 1983) |
 『定本 解析概論』(岩波書店, 2010) |
| これは,『初等整数論講義』に匹敵する名著と言えよう. 標題において「講義」とは銘打ってはいないものの, やはり文体は講義式であり, その意味では他の専門書に比して表現はやや冗長ではあるが, 講義の流れは自然であり, 内容に関しては一切の無駄がなく興味深いものばかりである. 「第一版 緒言」には, |
| 本書は, 著者の意図においては, 時代に順応した一般向きの解析学予修書, あるいはむしろ解析学読本で, なるべく少量の一冊子内において, 解析学の基本事項を大観して, 自由に各特殊部門に入るべき素養を与えることを目標とするものである. (中略) 予修書としての解析概論は繁冗を厭うて簡明を尊ぶことはもちろんであるが, 本書が著者の予想を裏切って意外に部厚になった一つの原因は講義式の叙述にある. 数学の解説法において, (中略) 一つをかりに教本式というならば, Euclid の幾何学原本がその典型とされ (中略) 既成の理論を整理して, それを論理的の系統に従って展開する方法で, その特色は正確と簡潔と, そうして難読とにある. (中略) 行と行との中間の空白を読むことを要するであろう (中略) 講義式は (中略) 数学上の概念発生の源をたずね, 理論進展の跡を追う方法で (中略) 数学を活き物として, その生長の一つのフェイズを捕らえようとするところに若干の新鮮味があり得るであろう. |
|||
| と述べてある. 展示化石のような無味乾燥な数学ではなく,『初等整数論講義』と同様, 貞治自身の裡から湧き出てくる活きた数学を味わえるのである. 目次からその内容を概観すると, |
| 第1章 基本的な概念 (実数の連続性, 数列の極限, コーシーの判定法, 連続函数の性質) 第2章 微分法 (種々の微分, 偏微分, 全微分, 極大極小, 接線, 曲率) 第3章 積分法 (求積法, 定積分, 原始関数, 広義積分, 種々の積分, ルジャンドルの球函数, 不定積分, 曲線の長さ, 線積分) 第4章 無限級数 一様収束 (種々の収束, 収束判定, 二重級数, 無限積, 巾級数, 種々の函数) 第5章 解析函数 特に初等函数 (コーシーの積分定理, 積分公式, 解析函数のテイラー展開, 解析接続, 有理函数の積分論, ガンマ函数, スターリングの公式) 第6章 フーリエ式展開 (フーリエ級数, 函数系の直交化, 相加平均総和法 (フェイエールの定理), 連続函数に関するヴァイエルシュトラスの定理, 積分における第ニ平均値定理, フーリエ級数に関するディリクレ-ジョルダンの条件, フーリエの積分公式) 第7章 微分法の続き (陰伏函数, 曲線の方程式, 曲面の方程式, 包絡線, 陰伏函数の極値) 第8章 多変数の積分法 (二次元以上の定積分, 多変数の定積分によって表される函数, 曲面積, 曲線座標, 面積分, ガウスの定理, ストークスの定理, 完全微分の条件) 第9章 ルベーク積分 (加法的集合族, ルベーグ測度論, ボレル集合, 累次積分, リーマン積分との比較, スティルチェス積分, ヴィタリの被覆定理, 加法的集合函数の微分法, 有界変動・絶対連続の点函数) 附録 (I) 無理数論 (有理数の切断, 実数の連続性, 極限, 巾根, 複素数) 附録 (II) ニ, 三の特異な曲線 |
|||
| となる. 他書にはあまり類を見ないが,『解析概論』には, 目次の直後に「定理索引」なるものが付されている. 残念ながら定理番号とページ番号のみの記載であるため, 内容までは直ちには判断できない. 次に示すように, 内容を明記した索引であれば, より読者への便宜となるであろう. 試みに, 第1章に現れる定理を全て挙げてみよう. |
| 定理1. 実数の切断は, 下組と上組との境界として, 一つの数を確定する [Dedekind の定理]. | |||
| 定理2. 数の集合\(\,S\,\)が上方 [または下方] に有界ならば\(\,S\,\)の上限 [または下限] が存在する [Weierstrass の定理]. | |||
| 定理3. 収束数列の部分数列は, もとの極限値に収束する. | |||
| 定理4. \(a_n\!\to\!\alpha\,\)ならば, \(|a_n|\!<\!M\,\)なる定数\(\,M\,\)がある. そうして\(\,|\!\:\alpha\!\:|\!\geq\!M\). | |||
| 定理5. \(\{a_n\},\{b_n\}\,\)が収束するとき, | |||
| (1) \(\displaystyle{\lim_{n\to\infty}(a_n\!+\!b_n) =\lim_{n\to\infty}a_n\!+\!\lim_{n\to\infty}b_n}\). (2) \(\displaystyle{\lim_{n\to\infty}(a_n\!-\!b_n)= \lim_{n\to\infty}a_n\!-\!\lim_{n\to\infty}b_n}\). (3) \(\displaystyle{\lim_{n\to\infty}(a_n b_n)= (\lim_{n\to\infty}a_n)(\lim_{n\to\infty}b_n)}\). (4) \(\displaystyle{\lim_{n\to\infty}(a_n/b_n)= (\lim_{n\to\infty}a_n)/(\lim_{n\to\infty}b_n)}\). |
|||
| 定理6. 有界なる単調数列は収束する. | |||
| 定理7. 閉区間\(\,I_n\!=\![\!\:a_n,b_n]\:(n\!=\!1,2,\cdots)\,\)において, 各区間\(\,I_n\,\)がその前の区間\(\,I_{n-1}\,\)に含まれ, \(n\,\)が限りなく増すとき, 区間\(\,I_n\,\)の幅\(\,b_n\!-\!a_n\,\)が限りなく小さくなるとすれば, これらの各区間に共通なるただ一つの点が存在する. | |||
| 定理8. 数列\(\,\{a_n\}\,\)が収束するための必要かつ十分なる条件は, 任意の\(\,\varepsilon\!>\!0\,\)に対応して番号\(\,n_{{}_{0}}\,\)が定められて, | |||
| \(p\!>\!n_{{}_{0}},\:q\!>\!n_{{}_{0}}\) なるとき \(|\!\:a_p\!-\!a_q\!\:|\!<\!\varepsilon\) | |||
| なることである. | |||
| 定理9. 有界なる無数の点の集合に関して, 集積点が必ず存在する [Weierstrass の定理]. | |||
| 定理10. 有界なる閉集合の列\(\,S_1,S_2,\cdots\,\)において, | |||
| (1) \(S_1\!\supset\!S_2\!\supset\!\cdots\!\supset\!S_n\!\supset\!\cdots\) (2) \(n\,\)が限りなく増大するとき, \(S_n\,\)の径が限りなく小さくなる |
|||
| ならば, これらの集合\(\,S_n\,\)に共通なる点がただ一つ存在する. | |||
| 定理11. 無数の円の一組が, 全体として, 有界なる閉集合\(\,F\,\)を覆うならば, \(F\,\)はすでに, それらの円の中の有限個だけで覆われる [Heine-Borel の被覆定理]. | |||
| 定理12. 或る区間において連続なる函数\(\,f(x)\,\)が, この区間に属する点\(\,a,b\,\)において相異なる値\(\,f(a)\!=\!\alpha,\,f(b)\!=\!\beta\,\)を有するとき, \(\alpha,\beta\,\)の中間にある任意の値を\(\,\mu\,\)とすれば, \(f(x)\,\)は\(\,a,b\,\)の中間の或る点\(\,c\,\)において, この\(\,\mu\,\)なる値を取る. すなわち | |||
| \(a\!<\!c\!<\!b,\:f(c)\!=\!\mu\) | |||
| なる\(\,c\,\)が存在する [中間値の定理]. | |||
| 定理13. 有界なる閉区域\(\,K\,\)において連続なる函数\(\,f(P)\,\)は有界で, かつその区域において最大および最小の値に到達する. | |||
| 定理14. 有界なる閉区域\(\,K\,\)において, \(f(P)\,\)は連続とする. 正なる\(\,\varepsilon\,\)が任意に与えられたとき, それに対応して正なる\(\,\delta\,\)があって, 区域\(\,K\,\)の任意の点\(\,P,Q\,\)に関して | |||
| \(PQ\!<\!\delta\) なるとき \(|\!\:f(P)\!-\!f(Q)\!\:|\!<\!\varepsilon\) | |||
| になる [連続の一様性]. | |||
| 第1章で提示されるのは, 以上の14定理である. 学生時代の私は, 内容を明記した (上掲のような)「定理索引」を, 数学書を繙くたびに作成していた. 一般に, 数学書 (演習書や解説書や啓蒙書などを除く) は一読して理解できるものではない. 従って, 初読の際は細部に拘泥せず全体を通読し, その際に,「定義索引」および上記のような「定理索引」をノートに作成する. その書籍における概要はこれで把握できる. 二回目は少し念入りに細部まで読む (定理における証明も丁寧に書き写す). それでも理解できない箇所は少なくない. これを, 三回目以降は精読をもって更に丹念に読む (章末の練習問題を全て解く時間的余裕はないが, 定理に該当するものは書き写す). これを繰り返すうち, 徐々に細部まで理解できるようになる. ―― 私自身が数学書を繙く際に適用してきた読書法はこれである. 最初から精読して全てを理解しようとすると大抵は挫折する. 適当な間隔をおいて幾度か丁寧に読み返すことが, 数学書を理解するには最も有効であろう. 巷間には, 再読する気になれない (無味乾燥な) 数学書も存在するが, 貞治の著書の場合は,「読み返すたびに新たな発見があ」ると先に述べた通りである. ところで, 上掲の定理は全て, 理工系学部においては大学初年度で必ず修得すべき基礎事項である. これらを導く貞治による叙述は全般に亘って簡単明瞭であり, 疑問を挟む余地は全くない. とは言え, 貞治の叙述が明快であることと読者がその内容を明晰に理解することとは, 全く別の話である. より高度の厳密性を追求する読者ならば, 貞治の解説をさらにキメ細かなものにすべく, 上記の各定理の間に補助定理 (補題) を設けるであろう. 定理以外の箇所についても同様である. 例えば第1章の冒頭部において, 貞治は, \(n\,\)次元ユークリッド空間の点\(\,P,P^{\prime\!},P^{\prime\prime}\,\)について, 三角不等式\(\,PP^{\prime}\!+\!P^{\prime}\!P^{\prime\prime}\!\geq\!PP^{\prime\prime}\,\)を (根拠を示すことなく) 掲げている. 貞治の記載方法はあくまでも明快である. 大学初級生でも何の疑問もたずに読み進めるに違いない. \(\mathbb{R}^2\,\)や\(\,\mathbb{R}^3\,\)における直観的に明白な三角不等式は (高校生でも) 知っているからである. しかし, \(\mathbb{R}^n\,\)における三角不等式が成り立つ理由を問われた場合, 初学者の大半は説明に躓くであろう. 「明晰に理解する」とは,「与えられた定義が well-defined か, 与えられた条件ないし仮定は必要十分か, などを吟味し, これを根拠として, 記載事項ないし命題の真なる理由を一つ残らず論理的に説明できる」ことを意味する. 貞治が「緒言」に記した「行と行との中間の空白を読むことを要する」なる姿勢は, 教本式のみならず講義式で書かれた書籍に対しても必要であり, 後年に教え子達も述べているように (最終節参照), これは, 貞治が学生に対してたびたび注意を促したことでもあった. 『解析概論』は, 出版直後から現在に至るまで (恐らく最も) 人口に膾炙した数学書であるが, その読みやすさに比して, 真に理解することは容易ではないと言えよう. 無論, これは『解析概論』に限ったことではないのであるが……. 先に引用した「第一版 緒言」には続きがある. |
| 解析概論に取入れるべき材料の取捨が他の一つの困難な問題である. (中略) 一例として指数函数, 三角函数を取ってみる. (中略) その古典的導入法は, 全く歴史的, 従って偶発的で, すこぶる非論理的と言わねばなるまい. さて解析概論において, その歴史的発生を無視することが許されないとするならば, これらの函数の合理的導入法を述べる上に, 古典的導入法が偶発的である所以をも説くことが, 解析概論に課せられる迷惑な任務というものであろう. (中略) 本書が理想的の薄さに止め得なかった他の原因がここにある. 基礎的の事項に関してはなるべく論証の明確を努めて, 応用的の部門においては解法の敏活を主として, 微細な論点を読者の補充に委任した. 各章の終りに少数の練習問題を配置して, 読者の任意使用に供したが, 精選を期したのではない. 解法の示唆を附記して置いたけれども, 誤算の有無は保証されないのだから, もとより拘泥すべきではない. (後略) |
|||
| 『解析概論』を執筆した当人しか体験し得ない苦心談がここに吐露されている. それまでの解析学書における表記法や証明法に創意工夫に満ちた改良を施し, 過不足のない洗練された内容と生の講義を髣髴とさせるような格調の高さにより, 出版後87年もの期間 (2025年時点で) に亘って読み継がれ, 多くの数学徒を感化してきた数学書である. しかし, 進化発展し続ける長い数学史の中では, その内容や視点に関して次第に経年劣化していく面が生ずることは已むを得まい. 直接的に貞治に教えを受けていない者達 (数学者を含む) から見れば, 貞治は数学史上において既に伝説化 (神格化) された存在である. それに対する感覚的な「憧憬」や「反発」を抱く者が多いことは頷ける. 「憧憬」ならば問題はない. 数学的に向上途中にある数学徒にとって前向きな動機となり得るからである. 障害となるのは「反発」の方である. これは多くの真面目な数学徒を困惑させ誤解させる可能性があり, 実害が生ずる. 実際, 後の時代の (貞治に師事していない) 数学者達による『解析概論』に対する批判は少なくない. 例えば, 微分方程式の章が存在しないのは (物理への応用が利かず) 片手落ちである, あるいは, 増訂版における (木に竹を接ぐような, または, 講義式ではなく教本式に書かれた) ルベーグ積分の後づけは初版が有していた全体の統一性を崩した, などという構成法に関する批判がある. また, 方法論に関する批判, 例えば実数の連続性 (p.3) や弧長を含む不等式 (p.21) における条件不備を初めとする, 各所に対する記述の改正を要求するものもある. 貞治がこれらの批判を考慮しなかったわけではあるまい. それでもなお, 一般の数学徒に対して「解析学の基本事項を大観して, 自由に各特殊部門に入るべき素養を与えること」を敢えて優先させ,「微細な論点を読者の補充に委任し」て『解析概論』を纏めたのである. そこに, 貞治が苦心談を書かざるを得なかった所以がある. 余談であるが, SNS上では, 自身の数学力を過信した者達 (多くは数学科出身者か?) による誹謗中傷も少なからず目につく. 彼らの皮相的感情的な物言いから判断して, (上記に述べたような) 一部の数学者達による批判を鵜呑みにして便乗したに過ぎず, 彼ら自体は,『解析概論』を自身の力では読めていない (内容を理解してはいない). 上記の苦心談の吐露を含め, 貞治が随所に見せた (本稿でもたびたび指摘してきた)「数学に対する謙虚な姿勢」を, 彼等にも見習って頂きたいと思う. 畢竟,『解析概論』を真に批判できる者は, これを凌駕する解析学書を書いた者以外にはないのであろう. そして, そのような偉業を成し得た者は, 今現在に至るまで一人も存在していない. これまでに出版された夥しい数の解析学書の中でも, 例えば, |
| [一松] 一松信『解析学序説 上・下』裳華房, 1962-1963. | |||
| [赤1] 赤摂也『微分学+積分学』数学セミナーリーディングス, 日本評論社, 1973. | |||
| などは, 随所に工夫が施されている名著であるとは思うが, とは言え, (あくまでも私の主観であるが)『解析概論』を凌駕しているとまでは言えない. ……斯く言う私自身は, (言うまでもなく) 貞治に対する感覚的な「憧憬」の念を抱く輩の一味である. 『解析概論』における講義式の流暢かつ平易な論理の流れは, この書を大変に魅力的なものにしている. さらに,『代数学講義』や『初等整数論講義』と同様, 各種多方面の趣向を網羅するような重要かつ典型的な例題 (章末問題を含む) が充実している点も大変に魅力的と言えよう. それらは, 修学のための演習問題であることは無論であるが, 寧ろ, 時間を掛けて鑑賞すべき美術品と言ってよいものである. 『解析概論』が魅力的な書物であるもう一つの大きな理由は, これも他の著書と同様, 貞治の数学思想が随所に垣間見えることである. 以下, 少し抜粋してみよう. |
| 内点, 外点, 境界点は直感的ないい表わしであるが, それらの定義を (中略) すなおに受け入れて, 論理的に考えるならば, (中略) '非常識' な場合も容易に承認されるであろう. このような論理的の態度が解析学の理解に絶対的に必要であって, それがなくては, 応用が不安心であろう. (p.29) | |||
| 曲線とは何をいうか. (中略) 便宜上幾何学的の用語を使うけれども, 空間的の直観を論理の根拠とはしないつもりだ (後略). (p.32) | |||
| 面積を使って, むぞうさに原始函数を出してしまったが, 原始函数の存在が問題になるならば, 面積の可能性も同様でなければならない. 我々は無頓着に面積, 体積などといっているが, そもそも面積, 体積とは何を意味するか? (p.90). | |||
| §8, [例7] の函数は (中略) 任意の小区間内に不連続点が (無数に) ある. それでも積分可能!(p.96) | |||
| 微分積分法の基本公式は (中略) 連続函数に関する限り, 微分と積分とが互に逆な算法であることを意味する. もしも連続性を仮定しないならば, この関係は成立しない. (中略) 連続函数以外では, 微分積分法はむずかしい!(pp.101-102) | |||
| 各所に挟まれる貞治の私見や感想は, 読者側に積極的な問題意識を誘発させるであろう. このような文言に啓発されて, 読者は自発的な関心をもって先を読み進めることになるのである. |
| 連続性を仮定しないで, 積分可能の条件を確定したのは Riemann (1854) であろう. (中略) Riemann 積分法からの, これより以上の収穫は, \(f(x)\,\)が有界ならば, 無数の不連続点があっても積分可能でありうるということの認識であるが, Riemann 積分法は積分論を終結させるのではない. 20世紀に入って, Lebesgue 積分論が出現してからは, Riemann 積分は中間的の存在になってしまった. ここでは, しばらく伝統に従って, Riemann 積分論を比較的に重く取り扱ったのである. (pp.109-110) |
|||
| ここに述べられていることは, 先述した [Gauss1] と [Lagrange] のような関係とは異なる. ルベーグ積分の出現によりリーマン積分の立場が「急転直下」したわけではない. (第ニ) 余弦定理の存在とは独立に三平方の定理が有用であるのと同様である. 貞治は「中間的の存在」と表現しているが, そこまで曖昧模糊とした立場に貶められてはいまい. これに関して貞治は, 増訂第二版における「序文」において |
| Lebesgue 積分論は, 組立てにおいては, Saks に従い, 細目に関しては, Lebesgue の原著のほか, de la Vallée Poussin, Carathéodory, Hahn, Kolmogoroff 等を参考にして書いたが, (中略) Lebesgue 積分論の追加に伴って, 109頁に述べたような意味における Riemann 積分論の縮小は当然考えられるべきであったが, 伝統を顧慮してしばらく原形を存することにした. | |||
| と記している. 無論, 執筆当時における事情を述べたものであるから, 現代の視点から『解析概論』の構成法を批判されることは, 著者貞治にとっては心外というものであろう. 続きを見てみよう. |
| 条件収束の級数は, 項の順序を適当に変更して, 任意の和に収束せしめ, または収束性を失わしめうることを, Dirichlet (1829) が指摘した. (中略) 収束性を度外において, 無限級数を有限級数のように放漫に取扱って, しばしば不可解の矛盾に逢着したことは, 18世紀数学の苦い経験であったのである. (p.146) | |||
| 初等数学では, 指数函数\(\,a^x\,\)は任意指数\(\,x\,\)に関する巾として定義せられ, その逆函数として対数\(\,\mathrm{log}_ax\,\)が導かれる. 特に\(\,e^x\,\)の底\(\,e\,\)は\(\,\displaystyle{\lim_{n\to\infty}\!\left(\!1\!+\!\frac{1}{\!\:n\!\:}\!\right)^{\!\!\!\:n}}\,\)として定義された. これは指数函数の歴史的の発生で, その理論はかなり複雑といわねばならない. (p.189) | |||
| 今かりに微積分法の発見以前に, 三角函数が知られていなかったと想像するならば, 円弧の計算の必要上, 自然に積分\(\,\displaystyle{\theta\!=\!\!\int_{0}^{x}\!\!\frac{dx}{\!\sqrt{1\!-\!x^2\!\:}}}\,\)に遭遇したであろう. 青年 Gauss (1797) はレムニスケートの弧長に基づいて (中略)\(\,\displaystyle{\int_{}^{}\!\!\frac{dx}{\!\sqrt{1\!-\!x^2\!\:}}}\,\)を考察して, 楕円函数発見の糸口を得たのである. (p.193) | |||
| 実変数に関する三角函数, 双曲線函数は複素変数に関する指数函数の一断面にほかならないから, それらの逆函数がすべて対数函数に包括されるのである. この認識は大切である. (p.198) | |||
| これらの記述は, 現今の数学で用いている用語や定理が解析学史においてどのように発生発展してきたかを知る契機となるものであり, 読んでいて大変に面白い. 他の解析学書においてこのような記述を見る機会は稀である. 第5章「解析函数」は『解析概論』の中で最も充実した (高密度の) 解説が展開されていると言えよう. その流暢な論理性の素晴らしさは言うまでもないが, 随所に現れる貞治自身の解析函数に対する讃辞が読者の心を揺り動かすのである. 一般数学者にとってはこれらの諸理論は既に当然のこととして理解されるものであろうが, 貞治は初学の数学徒の知的好奇心を刺戟すべく自ら新鮮な感覚をもって解析函数の萌芽と成育状況を叙述したのである. 恐らく, 実際の講義でも同様の表現をもって学生達を刺戟したことであろう. |
| 変数を複素数にまで拡張すること (中略) それによって古来專ら取扱われていたいわゆる初等函数の本性が初めて明らかになって, 微分積分法に魂が入ったのである. (p.201) | |||
| 微分可能といえば, 一語簡単であるが, 含蓄は多大である. だから有理函数や巾級数やに関しても, その '解析性' を伏せておいては, 真相がわかるものではあるまい!(p.204) | |||
| 実変数の函数においては, 微分がとかくめんどうで, 積分は一般に簡単であった. (中略) 解析函数の世界では, 正則性は微分しても積分しても動揺しない. そこに解析函数の実用性がある. (中略) 複素数の世界では, 微分可能も積分可能も同意語である. 驚嘆すべき朗らかさ! Cahchy およびそれに先だって Gauss が虚数積分に触れてから約百年を経て, 我々はこの玲瓏なる境地に達しえたのである. (p.216) | |||
| この引用部に記されたコーシーの定理の応用として, ディリクレ積分 (p.223) やフレネル積分 (p.224) が例として掲げられる. |
| 或る一点の近傍において与えられた解析函数は, それの解析的延長が可能なる全領域において一定であるから, 拡張の及ぶ限り一定の法則によって支配される (中略). 18世紀には (中略) 各函数は天賦の法則に支配されるものと信ぜられた. それを Euler 式の連続性という. (中略) 無意識的に夢想されていた法則上の連続性が解析函数によって, 最初の一例として, 実現されたのである. (p.229) | |||
| 解析的延長を遂行するならば, 全局においては函数の一意性が失われることが可能である. (中略) このような意味での解析函数の多意性は本質的である. (p.229) | |||
| 解析的延長の原則によれば, \(e^z\,\)を拡張して解析函数を得るには, \(e^z\!=\!\displaystyle{\sum_{}\frac{z^n}{n!}}\,\)が唯一無二の方法であることが確定したのである. \(\sin z,\cos z\,\)等に関しても同様である. (p.230) | |||
| 初学者にとって, 解析接続の概念はそれまでの関数の概念を大幅に刷新するであろう. 貞治の叙述は読者に対してその魅力を充分に (文学的な表現をもって) 伝えるものであり, 読者を飽きさせない推進力に富んだものである. さて, 貞治の叙述に惹かれて引用部分が大分長くなったから, 最後に「附録 (II)」における「各所で微分不可能なる連続函数」に触れて次へ進むことにしよう. 貞治は, 微分可能性の必要条件たる連続性が十分条件でない実例として, ヴァイエルシュトラス函数 |
| \(\displaystyle{f(x)\!=\!\sum_{n=0}^{\infty}\!a^n\!\cos\!\:(b^n\pi x)}\:\:(0\!<\!a\!<\!1, \:\:b\!=\!2k\!-\!1\,(k\!\in\!\mathbb{N}),\,\:ab\!>\!1\!+\!\frac{3}{\!\:2\!\:}\pi)\) |
| について言及し (p.39), 附録 (II) において, 同様の例の一つとして (線分の三等分線から得られる正三角形を或る規則で順次付加することで得られる) コッホ曲線を解説した (p.470). その後, 貞治は次のように記している. |
| このような曲線があるから, 各所で微分不可能なる連続函数があるといっても, もはやそれは驚くに足るまい (p.39頁参照). このような函数の簡単なる実例を, 筆者はかつて二進法を用いて作った (東京数学物理学会記事, 1903). その後, van der Waerden 君は, 十進法によって, 全く同様な函数を発表した (Mathematische Zeitschrift, 32, 1930). | |||
| ここにおいて貞治が嘗て作った二進法による実例とは, 前節に掲げた [高木3] を指す. いわゆる「高木函数」と称されるものである. 前掲の『定本 解析概論』(pp.509-517) においては, [高木3] に関する丁寧な解説が新たに附記されている (黒田成勝『いたるところ微分不可能な連続函数について』). 現在では, フラクタルの例として頻繁に引用される「高木曲線」であるが,「類体論」と同様, 発表当時は国内外においてほとんど知られていなかったらしい. これに関して, 末綱恕一 (前出) は, |
| [末綱] 末綱恕一『論文紹介』/『日本數學物理學會誌』 第8卷第8號 (1934年), pp.302-305. | |||
| におけるランダウ (Edmund Landau, 1877-1938) の著書『微分積分學初歩に就て』 |
| [Landau] E.Landau "Einfuhrung in die Differentialrechnun und Integralrechnung" P. Noordhoff N. V., 1934, 全368頁. | |||
| に関する書評の中で, |
| 第五章に於いて愈〃導函数\(\,f^{\prime}(x)\,\)を導入する. \(f^{\prime}(x)\,\)を定義すると直ぐに, 到る所連續で何處でも微分出來ない函数 (Weierstrass の定理) を例示する: | |||
| \(\displaystyle{f(x)\!=\!\sum_{n=0}^{\infty}\frac{\{4^nx\}}{4^n}}\:\: (\{y\}\,\)は\(\,y\,\)と之に最も近い整数との距離\()\) |
|||
| 著者は之を今日最も簡單な例で van der Waerden のものと云つて居るので事實\(\,4\,\)を\(\,10\,\)で置換へれば van der Waerden が近頃出したものに相違ないけれども, \(4\,\)を\(\,2\,\)で置換へるならば之は高木先生が數物記事の第一卷に出されたものに外ならない. Landau も van der Waerden もこの卅一年前の論文には全く氣が付かなかつたのであらう. | |||
| と記している (pp.302-303). 貞治は恐らく [Landau] に目を通しているはずである (後節 (§5-6) で触れる『微積の体系といったようなこと』の中で言及される) から, この箇所におけるランダウの記事に関しては苦笑させられたことであろう. |
| 前掲の三部作『代数学講義』,『初等整数論講義』,『解析概論』は全て, 東大における貞治の講義に基いて執筆された著作であったが,『代数的整数論』は, 大学での講義とは無関係に執筆された著作である. 執筆当時, 貞治は67歳であった. 実際, 貞治が大学で類体論を継続的に講義することはなかったらしい. 菅原正夫は,「先生は類体論の講義をされたことはありません.」と断言している (前掲書 [追想高木] p.222). 河田敬義『わたしの好きな数学史』(同書, p.172) には,「大学では類体論の講義もなかった」と記されているが, 森茂雄『書物は手元に』(同書, p.68) には,「先生の「新著解説」なる講義の一環として (中略) 類体論の講義をされました. おそらく類体論を取り上げられたのは後にも先きにもこの一回だけではないでしょうか」と記されている. また, 彌永昌吉は「東大の最終学年 (1928-29) と大学院では先生のセミナーで類体論を勉強した」と述べている (『類体論50年』(前掲書 [彌永1], p.25)) から, 部分的には大学で採り上げられることはあったのであろう. 私が所蔵するのは, 1994年に発売された重刷版 |
| 『代数的整数論 一般論及類体論』第2版, 岩波書店, 1971, 全307頁. | |||
| である. これは, 私の学生時代には長らく品切れ状態であった. そのため大学生協や近隣の小売店を通して何度も繰り返し発注した後に, ようやく入手したものである.
以下, 引用は全てこの書籍からのものとする. |
 『代数的整数論』岩波書店, 1971 |
| 既に述べたように,『解析概論』は, 貞治自身の監修による岩波講座 "数学" 全30巻 (1932-1935) に掲載された. 一方,『代数的整数論』もまた同講座において発表され, 後に単行本化されたものである. 副題にもある通り, この著書は, 前篇「一般論」と後篇「類体論」から成り, 詳細なる構成は |
| 前篇 一般論 第1章 代数的整数 (代数体の定義, 代数的整数の性質) 第2章 代数体の整数「イデアル」(イデアルの性質, イデアル論の基本定理, イデアル因子) 第3章 剰余類 (イデアルを法とする剰余類, 剰余類の四則, 剰余類環\(\,\mathfrak{R}(\mathfrak{m}),\,\mathfrak{R}({\mathfrak{p}}^m)\)) 第4章 「イデアル」の類別 (分数イデアル, イデアル類群と類数) 第5章 ミンコフスキの定理の応用 (ミンコフスキの定理, 代数体の判別式) 第6章 相対的の体 (代数拡大\(\,K\!\!\:/k\), イデアルの延長, 共役体, \(K\!\!\:/k\,\)における素イデアル\(\,\mathfrak{P}\!\subset\!K\)) 第7章 判別式 共役差積 (代数体の共役差積, 相対判別式, デデキントの判別定理) 第8章 ガロア体 (分解体, 惰性体, 分岐体, 円体, クロネッカーの定理) 第9章 単数 (ディリクレの単数定理, ガロア体の単数) 第10章 素数進法 (\(\mathfrak{p}\,\)進法, ヘンゼルの補題, \(\mathfrak{p}\,\)の\(\,n\,\)冪剰余) |
|||
| 後篇 類体論 第11章 合同類別 (エルブランの補題, 狭義イデアル類, イデアル群の導手) 第12章 解析的の考察 (合同類別における各類のイデアル密度, 代数体の\(\,\zeta\,\)函数, 類体と円分体) 第13章 基本定理 (アーベル体の基本定理, ノルム剰余と群指数, 結合定理, 類体の一意性) 第14章 分解定理 同型定理 相互律 (アルティンの相互律, 推進定理) 第15章 存在定理 導手定理 (クンマー体, その素因子分解と導手, アーベル体の導手, ハッセの導手公式) 第16章 終結定理 (チェボタレフの密度定理, 終結定理) 附録 (1) 二次体論 (2) 円分体の類数 (3) イデアル論の基本定理 補遺 |
|||
| となっている. この著書にある類体論の概要については前節で既に述べているので, ここでは割愛する. 「序」を見ると, |
| 著者が, 1915年以来, 日本数学物理学会記事に断片的に掲載した数編の論文を綜合して, 1920年, 手王匡帝国大学理学部紀要に類体論の全貌を発表してから,
既に四半世紀の星霜を経た. 其の間, (中略) ドイツの少壮数学者 Artin 及び Hasse によって, 類体論の整理簡約が行われたが,
就中 Artin の相互律の発見は類体論への喜ばしい貢献であった. 次で, 珍しくもフランスから, 二人の青年数学者 Herbrand 及び Chevalley が参加して, 整理簡約が進められた. 本書に掲げた類体論の基本定理及び存在定理の証明法は Herbrand に拠り, 又相互律は Chevalley の証明法に従った. 類体論の成果は, 基本定理・分解定理・同型定理 (相互律)・存在定理, いずれも極めて簡単明瞭であるに反して, その証明法は, 上記諸家の努力にも拘らず, 今なお紆余曲折を極め, 人をして倦厭の情を起こさしめるものがある. 類体論の明朗化は, 恐らくは, 新立脚点の発見に待つ所があるのではあるまいか. |
|||
| とある. また, 黒田成勝による第2版の「序」には, |
| 著者高木貞治先生が, 本書の初稿を岩波講座数学に執筆されて以来, それが整数論研究者の精神を力強く高揚して来たことは言うまでもない. 一方微細な点では, 大局の美に魅せられて, 難読難解, 時には誤読誤解をさえ生じた箇所もあった. それらは著者の余りにも高度の暗示的叙述からも, また読者の受容の不全からも生じた. | |||
| とある. 前篇「一般論」は明快で理解しやすいが, 肝心の後篇「類体論」は, 貞治の叙述に問題があるわけではないのであろうが, 大変読みづらく, 理解しがたい部分が少なくない. 無論, 貞治自身の論文 [高木13] における複雑な論理展開に比べれば改善が見られるのであるが……. 貞治自身が「紆余曲折を極め, 人をして倦厭の情を起こさしめる」と述べた所以であろう. フルトヴェングラーや貞治が素数冪の次数に関する相互法則を示したのに対し, アルティンやハッセが一般冪剰余の相互法則を示したことは既に述べた. シュヴァレーが類体論の算術的証明を得たことも既に述べている. 貞治の「序」に登場するエルブラン (Jacques Herbrand, 1908-1931) は, 僅か23歳で事故死した異才の数学者であり,「種の理論」や「一般単項化定理」を含む類体論関係の優れた論文を発表したことで知られている ( [彌永8], p.127). 貞治が「珍しくもフランスから」と述べたのは, かつてのストラスブールでの一件が念頭にあったのであろう. とは言え, 理解困難な貞治の理論が, ドイツやフランスにおける新進気鋭の若手数学者に理解され, 簡約化や算術化が促されたことが, 類体論が人口に膾炙する大きな機縁となったことは間違いない. その辺りの事情を, 貞治は「喜ばしい貢献」と表現したのである. 以下, この著書に見られる貞治の数学思想をいくつか拾ってみよう. まず, 証明における方法の純粋性について――. 第2章における「定理2」すなわち「整係数多項式の積の各係数が\(\,\lambda\,\)の倍数ならば, もとの多項式の各々の係数の積も\(\,\lambda\,\)の倍数である」に関して |
| (前略) 上記証明法は簡明のようでも, 方法上不純な所があることを, 読者は不快に思うであろう. (中略) 目的の為に手段を問わない感がある. (p.19) | |||
| と述べ, クロネッカーの整数論の基礎である定理「多項式の積のイデヤル因子は各多項式のイデヤル因子の積に等しい」に関しても |
| この定理 (多項式の積のイデヤル因子は各多項式のイデヤル因子の積に等しい) は Kronecker の整数論の基礎である.「イデヤル」論を使えば, その証明は上記の通り簡単である. この後もこの定理を用いて, 証明を短縮し得る場合があるから, 変数は方法上不純ながら併用する. (p.26) | |||
| と述べる. 論文ではなく書物として執筆する場合, 数学的に純粋 (自然) な方法よりも, より簡明な (晦渋でない) ものを採用せざるを得ないということであろう. 一方, 技術的な問題で回避し得ない方法について, 第7章の冒頭部において |
| 吾々は今代数的整数論に於て解説の最も難渋なる一章に入る. 問題は古くて, しかも基本的であるのに, 整理が不行届で, 心持がよくないのである. (p.61) | |||
| と述べ, デデキントの判別定理に関しても |
| この定理の証明は非常に困難であったが, (中略) Hensel (1894) が Krinecker の形式論を用いて比較的に簡単なる証明を与えた. (中略) この方法によって, 2(共軛差積の性質) は容易に得られない. 且又数体\(\,k\,\)の問題を不定文字 (Unbestimmte) を含む整域\(\,k\,[\!\:u_{{}_{1}},\cdots,u_m\!\:]\,\)に引入れるのは, 方法上不純である. (中略) 本書では冗長を厭わないで, いずれの立脚点にも偏倚しないで, 凡ての方法を紹介したのである. (p.82, pp.86-87) | |||
| と述べている. 附録 (3) には,「イデアル論の基本定理」(p.22) の証明に用いた予備定理 (p.18) について, |
| この定理の証明は Dedekind が Dirichlet の整数論講義第四版に附載したものの変形であるが, 既に Dedekind 自身が彼の証明に稍不満の意を表している.
Hilbert が Hurwitz の同僚として Königsberg 大学にあった時, 彼等は当時相携えて散策の途次, (中略) 一人は Kronecker
の証明法を論じ, 又一人は Dedekind の方法を語って, 両者共に厭うべきもの (scheusslich) なるものことに於て意見の一致を見た
(後略). Dedekind 以後, 上記予備定理の証明の簡易化が諸方面から試みられたが, 就中 Hurwitz の証明は, 着意の単純, 方法の妥当なる点に於て, 最も興味あるように思われる (後略). (p.291) |
|||
| とある. これらの言明からは, 貞治が, 証明の純粋性 (ないし単純性) に少なからず拘りを見せている様子が窺えよう.『髙等敎育代數學』において, (問題を解く際には) 単に正答を得ればよいのではない, 解法は単純明快を旨とせよと, 学生に注意を与えた貞治は, 定理の証明においても, 単に証明を得ればよいのではない, その方法は自然で妥当であることを旨とせよ, と述べているのである. 同様の言明は p.288-289 にも見られるし, 次節 (§5-6) で触れる『数学の自由性』においても現れる. 方法の不純性を上手く回避できず「倦厭の情を起こさしめる」にも拘らず「新立脚点を発見」できていないところに, 貞治の懊悩が垣間見えるであろう. また, 表記法や用語に関する注記も幾つか見られ, |
| 「イデヤル」を独逸字\(\,\mathfrak{a},\mathfrak{b},\mathfrak{c}\,\)などで示すのが慣例である. (p.16) | |||
| Landau の記号\(\,2\!\:|\!\:10\,\)は約数を必ず左, 倍数を必ず右に書くことが窮屈である. (p.20) | |||
| (分岐定数) \(v,v^{(1)},\cdots\,\)は Hilbert 報文 に\(\,L,\overline{\!\:L\!\:},\cdots\,\)と記すものである. 運用上は記号を変えて, これらを\(\,v\!+\!1,v^{(1)}\!+\!1,\cdots\,\)と書くのが便利なこともある. (高木, 紀要, 41, 9, §6) (p.100) |
|||
| \(s\sigma\!\:(K)\,\)などは (中略) \(K^{\sigma s}\,\)と書く方が都合がよいが, 印刷上の顧慮から函数記号式にしておいた. 故に\(\,s\sigma\,\)は始めに\(\,\sigma\), 次に\(\,s\,\)を意味する. (p.121) | |||
| (2) に於ける\(\,\mathfrak{m}\,\)は記号として「イデヤル」のように見えるが, それはただ\(\,\mathrm{mod}.\,\)としてのみ使用される.
(中略) それを標示するためには, Hasse のように, 記号\(\,\widetilde{\mathfrak{m}}\,\)を用いるのもよい.
(中略) 意図する所は概念の明確なる表示にある. 言葉では\(\,S_{\mathfrak{m}}\,\)を Strahl modulo \(\mathfrak{m}\,\)という. Strahl\(\!\:\)=\(\!\:\)rayon\(\!\:\)=\(\!\:\)ray\(\!\:\)=\(\!\:\)放射線. 本書では, このような fantastic な造語の邦訳を敢てしないで, 記号\(\,S_{\mathfrak{m}}\,\)を使う. (p.149) |
|||
| などのほか, p.106, p.142, p.146, などにもこの件に纏わる記載がある. ハッセが「基本定理」を「逆定理」"Umkehrsatz" と称したこと,「順序定理」"Anordnungssatz",「推進定理」"Verschiebungssatz",「終結定理」"Abschliessungssatz" がハッセの命名によるものであることも明記されている (p.174, p.194, p.199, p.246). さらに, 数学史上における逸話も幾つか紹介されている. |
| 解析的の方法によって (\(L\,\)函数)\(\,L\!\:(1,\chi_{{}_{i}})\!\not=\!0\,\)を証明したのは Hecke (1917) である. 一方, (合同群)\(\,H\,\)に対応する (類体)\(\,K\,\)が存在すれば, \(H\,\)に関する算術級数の定理が成立って, 従て\(\,L\!\:(1,\chi_{{}_{i}})\!\not=\!0\,\)である (中略) 類体論によって算術級数の定理が確定したとしても, \(L\!\:(1,\chi_{{}_{i}})\,\)の直接証明は当然希望されるものである. 興味のあるのは, 本来の Dirichlet の算術級数の定理は二次形式論によって1837年に証明され, それの解析的証明が Mertens によって1897になされたのに比較して, 一般的の場合に於て, 兩方面の証明が殆ど同時に出来たことである. (pp.171-172) |
|||
| 筆者は紀要論文 (27-62頁) で, 先ず素数次の環状体に関しての証明をして, 素数次の環状体を積み重ねて一般環状体に移乗した. その途も短くない.
素数次の場合の方法が直に一般の環状体に適用され得ることを指摘したのは, 不幸にして登山事故のために夭折した仏国の青年数学者 Herbrand である. (p.191) |
|||
| Artin の相互律は Hamburg の論文集 (Abhandlungen, 1927, 353頁) で発表された. その証明には, 当時の類体論の成果を用いている. (中略) この証明は若干簡易化されて, Hasse の報文 (II, 14-22頁) に載っている. 本書では, 多少躊躇の後, これらを凡て割愛して (直観性を犠牲にして), 相互律の直接証明法を述べることにした. (p.199) | |||
| その他, クンマー体\(\,k\,(\sqrt[l\!\:]{\omega\!\:})\,\)の歴史的位置づけ (p.217) や, クロネッカー式密度\(\,\varDelta(M)\,\)からチェボタレフの密度\(\,\varDelta(\varOmega)\,\)に至る歴史的経緯 (p.244), ディリクレによる二次体および円分体の類数計算に関する叙述 (p.260, p.278) も読者の興味を引くであろう. なお, 上掲の最後の引用箇所における「直観性を犠牲にして」なる所以は, シュヴァレーが, (円の\(\,m\,\)分体)\(K\,\)と (\(K\!\!\:/k\,\)から生ずる円分体)\(\,\varGamma\)とに交截法を二重適用して問題を円分体の場合に帰着させたことによる. 相互律は内容は簡明であるが, 証明は高度に技術的で暗中を驀進するようなものであった. 素でないイデアル\(\,\frak{a}\,\)に対するヤコビ-ハッセの記号\(\,\displaystyle{\left(\!\frac{K\!\!\:/k}{\frak{a}}\!\right)}\,\)が機械的ながらも証明の簡明さを齎す事実は,「類体論の根柢に内在する複雑性の顕現」である. \(K\!\!\:/k\,\)のイデアルのノルムが\(\,k\,\)における群を成すことは自然であるが, これを\(\,k\,\)の全てのイデアル群の部分群として考察することは「むつかしくて, 今の所, 手が着けられない」. しかし, \(K\!\!\:/k\,\)がアーベル体であるときに限り, このノルムの群を\(\,k\,\)の合同群と併せてイデアル群\(\,H\,\)を作ることで類体論は成功したのであった (p.215). |
| それは奇妙だけれども, 事実であるから已むを得ない. そこに秘密があって, それが類体論の非素朴性ともいうべきものであろう. 記号\(\,\displaystyle{\left(\!\frac{K\!\!\:/k}{\frak{a}}\!\right)}\,\)はその秘密を吸収し,
陰蔽して外観上円滑に行動するのである. 古典整数論に於て Jacobi の記号は曾て Gauss の二次形式論の記述を短縮して, 同時にそれを秘密的にした. それは暗中模索の結果であろうが, その秘密は一般「アアベル」体論に由て暴露されてしもうたのである. さて今度は「ヤコビ」式の記号が再び類体論を機械化する. 素朴性と機械化の交代循環! |
|||
| 貞治はこの後も類体を定義する方法に関する興味深い記述を続ける. これらの言明を晦渋な本論と照らし合わせて読むとき, 類体論の煩雑性がもつ深淵かつ不可思議な様相に対する貞治の新鮮な驚嘆の念が読者を刺戟するであろう. 『初等整数論講義』と同様,『代数的整数論』の「附録」においても, 二次体および類数が扱われる. 貞治自身が「二次体論だけの直接の叙述は長たらしくなる」(p.249) と批判するところの『初等整数論講義』第5章の内容 (平方剰余の相互法則および種の理論) が, ここでは類体論の成果を援用して極めて簡明に纏められるのである. 円分体の類数およびガウスの和に関しても,『代数的整数論』の立場から見れば,『初等整数論講義』における叙述法は, 却って迂遠なる説明を余儀なくされている感を否めない. |
| この問題はそれ自身興味深いものであるが, 当時にあっては, 整数論代数学及び函数論の最高部門の交錯する数学の El Dorado である所に, 特に魅力があったのであろう. | |||
| と述べる.「特に魅力があったのであろう」と客観視しているが, 若かりし日の貞治もまた, その魅力に取り憑かれた者の一人であった. 続けて「単項化定理」を簡単に説明した後, |
| 虚数乗法論に於ける実例はこの定理の一般性を示唆するのであるが, ヒルベルトは唯\(\,K\!\!\:/k\,\)が2次の場合及び4次で環状でない場合にのみ証明をしたに過ぎなかった. その後, Furtwängler が群論化された形に於て一般的の証明を与えた. 単項化の問題は未だ成書に取入れられる程度にまで熟していない (後略) | |||
| と述べている. 上掲のフルトヴェングラーの業績については前節でも簡単に触れた. その後の展開については, 黒田成勝『高木貞治先生を敬慕して』(前掲書 [追想高木], p.243) において |
| Hilbert の単項化定理は, Iyanaga によって一般単項化定理にまで拡張せられた. これは単項化定理に関し, ちょうど, Hilbert の類体から先生の一般の類体への概念拡張に相応する拡張で, 先生門下から成しとげられたこの美麗な第一着の発展を, 先生はどんなにか喜びをもって迎えられたことであろう. その後この一般単項化定理のさらに興味ある考察が Tannaka などによって続けられている. | |||
| と記されている. 上掲の「Iyanaga」は, 前節に掲げた論文 [彌永3] であり,「Tannaka」とは, 淡中忠郎 (1908-1986) による |
| [淡中] T.Tannaka "An Alternative Proof of a Generalized Principal Ideal Theorem" Proc. Japan Acad. Vol.25, 1949, pp.26-31. | |||
| である. この件に関する淡中の業績は, 貞治が名誉議長として列席した「代数的整数論国際会議」(1955) における |
| [藤崎] 藤崎源ニ郎『本会議講演記録』/ 岩波書店『数学』第7巻第4号 (1956年10月), pp.203-239. | |||
| に詳しい. また,「単項化定理」に纏わるその後の状況については, |
| [三宅] 三宅克哉『彌永先生の数学的な業績』/ 日本数学会『数学通信』第11巻第2号 (2006年8月), pp.44-48. | |||
| に簡明なる解説がある. 『代数的整数論』の巻末には, 黒田成勝による「第2版 跋」がある. その末尾で「類体論」なる名称に関する貞治の懸念が言及されて, この著書は閉じられるのである. |
| 類体論は相対「アアベル」体論に他ならないので, 著者は類体論という名称が, 整数論になにか特別の理論があるような印象を与えやしないかと懸念されたかに見受けられるが, 漢字三字の三綴音である類体論という言葉は, 親み易い名目になっている. つまり, 類体論は, 現今の立場からは,「アアベル」体論なのである. | |||
| ~続く~ |
| ©Copyright 2025 SAKATA MASAHIRO. All Rights Reserved. |