| 評論・随筆・記録 |
| 管弦楽《名曲50選》 1994 | 管弦楽《続・名曲50選》 2004 |
| 西田幾多郎と京都学派 2001 | スティーヴ・ライヒの音楽 2024 |
| フェルマーの最終定理と未解決問題 2003 |
| 高木貞治と類体論 |
| 2025年 執筆 |
| 目次 |
| 岐阜県本巣市の南部に位置する「富有柿センター」内に「高木貞治博士記念室」は存在する. ここには高木貞治の業績や人柄を偲ばせる遺品や遺稿が数多く展示されており,
それらは専門家以外の者が見ても極めて興味深い. 殊に彼の自筆稿や遺墨には人間味が色濃く滲み出ており, 何度見ても感慨深いものがある. 多くの書籍に掲載されている彼の写真と併せて, 未踏の数学領域で格闘しつつ一心に研究を突き進めていく貞治の姿に想いを馳せるわけである. |
 高木貞治 (1875-1960) |
| ――上記の書き出しは, 拙稿『西田幾多郎と京都学派』(2001) の冒頭部に倣ったものである. そこで述懐した通り, 哲学者西田幾多郎 (1870-1945) は, その人物と業績を知るに及んで, 学生時代の私が非常に感化された学者であった. 一方, 数学者高木貞治もまた, その人物と業績から, 学生時代の私が大いに感化された学者であったのである. 小学校高学年から中学校時代にかけて国内外の文学に魅了された私は, 小説家を志すようになった. 固より算数や数学が苦手であった (先生の目を盗んで授業中でさえも小説を書いていた) 私は, 高校生になると, 小説家への前段階として (多くの小説家の前例に倣って) 国語科教員を目指すようになり, 文科系のクラスに所属した. 当時は, 文科系の国立大学の受験に必要な最小限の (不充分な) 数学の知識しか持ち合わせていなかった. そのような私が高木貞治に興味をもったのは, 大学の図書館で『初等整数論講義』を手にした時であった. 代数学の講義で「フェルマーの最終定理」の存在を知り, 興味をもって整数論に関連した書籍を探し始めたのである (その経緯については拙稿『フェルマーの最終定理と未解決問題』(2003) でも簡単に触れている). これを契機として都内の書店や古書店で専門書を渉猟するうち, 私は次第に数学に惹かれるようになった. 所属が教育学部であったことが幸いして, 国語専修から数学専修への編入を認められたのもこの頃の話である. 内容は後述するが,『初等整数論講義』は, 予備知識なしに読める数学書である. その第2版には, 貞治の娘婿である黒田成勝 (1905-1972) による序文 |
| 本書全般の記述, 特に著者自身の創設になる類体論の光輝のもとに, その最も身近かな具体的事例として解説された二次体論の記述は, 読者に強い感銘を与えるものである (後略) | |||
| が記載されている. この文言は印象的であった. 小説家を志していた私には, 文学で読者に感銘を与えることは理解できる. しかし, 数学で読者に感銘を与えるとは? このとき初めて, 数学というものには底知れぬ深い理論体系と魅惑的で美しい芸術的世界が存在することを漠然と感じた. 是非「類体論」なるものを理解したいと思ったわけである. その後の私は, 大学の講義で数学の基礎を学ぶ傍ら,『解析概論』や『代数学講義』などの数学書を繙いた. 併せて,『近世数学史談』や『数学雑談』などの啓蒙書や, 彼の門弟を初めとする種々の学者達による回想や評伝 (後述) を通じて, 貞治の人物や業績に魅了されていったのである. 前置きはこのくらいにしよう. 高木貞治なる人物が, 学者あるいは教育者として同世代や後世に対して如何に多くの影響を与えたか, 本稿では, その生涯と業績を紹介してみようと思う. |
| 高木貞治は岐阜県の旧大野郡数屋村 (現在の本巣市数屋) の出身である. 誕生したのが1875年4月21日であるから, 今年 (2025年) は貞治の生誕150年に当たる. 貞治は地元の一色小学校と旧制岐阜県岐阜第一中学校 (現在の岐阜県立岐阜高等学校) を卒業し, 京都の第三中学高等学校 (現在の京都大学) に入学するまでこの地で過ごした. |
 高木貞治の胸像 (本巣市立糸貫中学校敷地内) |
| 本稿の冒頭で紹介したように, 岐阜県本巣市の南部に位置する「富有柿センター」内に「高木貞治博士記念室」は存在する. 本節では, この「記念室」内にある「展示品」および |
| [本田] 本田欣哉『高木貞治の生涯』/ 日本評論社『数学セミナー』1975年1月号-6月号. | |||
| における評伝を軸として, まずは貞治の修業時代を見ていくことにしたい. この「記念室」を私が最初に訪れたのは, 1995年の春であった. 大学卒業と同時に私は山梨県甲府市内にある私立の中高一貫校に数学科の専任教諭として着任した. そのため, 当時の居宅は甲府市内にあった. 私は春休みを利用して車で甲府を発ち, 長野県の山道を経由して岐阜県へ入ったのである.「記念室」が設置されていた場所は, 現在の「富有柿センター」から3kmほど南に存在した本巣郡糸貫町の役場内にある狭い一室であった. そこでは貞治の幼少期の揮毫や学生時代のノートなどを間近で見ることができた. 簡潔な評伝と共に一部の遺品の写真が掲載された小冊子 |
| [高橋] 高橋巌『世界数学界 世紀の金字塔 高木貞治先生』高木貞治博士顕彰会, 1993, 全28頁. | |||
| を入手したもの, その時のことである. それから20年以上を経た2018年の9月に, 私は再び岐阜を訪れた. この年の3月に「記念室」が新装開設されたことを聞きつけたからである. それが「富有柿センター」であった. 今度は嘗てのような暗くて狭い一室ではなく, 清潔感のある開放的な空間に移り変わっていた. |
 「富有柿センター」外観 (岐阜県本巣市) |
| 「富有柿センター」には, 特産品の富有柿を加工する農産工研究開発室や柿に関する史料, 陶芸作品を閲覧できる展示ホールなどがあった. 建物の3階にある「記念室」には, 貞治の幼少期の写真や揮毫, 愛用の扇子や眼鏡, 胸像や賞状が展示されてあり, 2階部分の開放的な空間には, 学生時代のノートや雑誌に寄稿した回想録の自筆原稿などが展示されてあった. |
 「記念室」(「富有柿センター」3階) の一画 |
| 幸いにも撮影は禁止されていなかったため, 幾つかの展示品を撮影した. とは言え, 写真で見るのと実物を間近で見るのとでは, 筆遣いや素材の質感などの印象が全く異なる. 多くの教え子達によって伝説化され神格化すらされている感のある高木貞治であるが, 彼が架空や想像上の人物ではなく, 実在した生身の人間であったことが如実に伝わってくるのである. 貞治の出生前後は高木家における種々の事情が重なり, 貞治は母親 'つね' とその兄 '勘助' を養父として幼少時代を過ごした. 勤勉な役人であった勘助は貞治の教育には熱心で, 5歳になった貞治を隣家の医師宅で学ばせ, 漢文の素読をさせたという. 小学校時代の貞治は, 6年の小学校課程 (尋常科4年, 高等科2年) を, 飛び級制度をもって3年間で終えてしまった. その秀才ぶりはよほど周囲の大人達を驚かせ, 噂を広めさせたのであろう. 当時の地元の新聞 (岐阜日日新聞, 1886年1月7日) には貞治の「神童」ぶりが報じられているという (§6-1.参照). 展示品の中では, まず, 貞治が小学校時代 (10歳時) に書いた作文『蟻説』が目を引く. 力強い凛とした筆致もさることながら, そこに記された貞治の確固たる主張に感嘆させられるのである. |
 10歳の高木貞治が書いた作文『蟻説』 |
| 蟻ハ一小蟲ニシテ其種類甚タ多ク同類數千群ヲナシ毎群蟻王アリテ之ヲ統フ 其粮ヲ運フヤ荷身ニ十倍スト雖衆議蝟集シ詵々爭ハス孜孜怠ラス遂ニ之ヲ其巢ニ運フ 夏日炎々ノ時タリト雖終日怠ラス勉勵シテ粮ヲ求ムルニ從事ス (中略) 夫人怠惰放逸ニシテ後日困難ニ歎ク者往々之レ有リ 其レヲシテ蟻ノ行為ヲ目セシムレバ豈愧スベキノ甚シキニアラスヤ |
|||
| 蟻の勤勉なる様子 (その小さな身体を遥かに凌ぐ大きさであっても真夏の炎天下であっても倦まず弛まず無心に餌を巣へ運び冬に備える勤勉さ) を述べ,「人間の場合, 怠惰に過ごして後で嘆く者がしばしば見られるが, 蟻の行為と比べて如何に恥ずべきことであろうか.」と結んでいる. 同じく小学校時代に書かれた書画における精緻な筆遣いにも, 大いに感心させられるであろう. |
 |
 |
| 鉛筆画 (左) と書幅「松竹蒼と瑞靄懸」 | |
| デッサンの右上に朱書きされた数字は, 教師による評価点であろうか. 書幅は「松竹が青々と繁り, めでたい靄のかかった朝焼けの中を鶴が軽快に飛んでゆく. 新たに詩句をしたため新年を祝う. すなわちこれ年はじめの最初の句なり.」という, 貞治自身の創作による七言律詩である. |
| 1886年, 11歳で岐阜県岐阜第一中学校に進学した貞治は, 飛び級で小学校を卒用したために在校生の中では最年少であった. 年齢にして3歳以上もの差がある他の同級生 (上級生) に対して, 体力では全く勝ち目のなかった貞治であるが, 学業に関しては上級生達から一目置かれていたという. 彼らの数学の宿題を貞治が手伝い, 教師が出題した数学の難問を貞治だけは苦もなく解いてみせたからである. 経済的な理由から県議会で中学校廃止論が勃発した際, 上級生達が暴力も辞さない構えで議員達を威嚇しに行く一方で, 貞治は「欧米列強を向こうにまわして日本は立って行かなければならない. その人材を養う所が中学校である.」と県知事を相手に論じたらしい. 僅か13歳の貞治の説得が効いたらしく, 中学校は廃止を免れたのであった. 貞治の意外な一面が窺えるエピソードである. この時代に書かれた論説文や授業ノートも, 筆致および内容の点において目を見張らせるものがある. まず, 11歳時の論説文『善ヲ爲スコト最も樂シキノ說』を見てみよう. |
 11歳時の論説文『善を爲スコト最も樂シキノ說』(1886) |
| 人生ノ最モ快樂トスル所ハ善ヲナスニアリ (中略) 絲竹管絃ノ樂ハ人ノ耳目ヲ快爽ナラシムト雖モ以テ眞ノ樂ミトナスベカラス 然レトモ善ヲナスハ最も自己ノ心ヲ愉快ナラシム善ヲナスコト尤も樂シトハ其之ニアルカ |
|||
| 貞治自身の経験に即した主張なのか古人の言を引用したものかは判らない.「善」に関して論じている点では, 本稿の冒頭で触れた西田幾多郎にも,『善の硏究』(弘道舘, 1911, 全261頁) なる著作があるが, 出版年から判断して, その影響を受けて書いたものではないであろう. 「動物学」のノートにも, 精密に科類ごとの特徴が記載されている. |
 「動物学」の授業ノート |
| 袋獸類 此ノ目ニ属スル者ハ腹ノ外ニ袋狀ノ皮ヲ有ス其ノ子ヲ生ムトキハ其ノ袋内ニ於テ哺乳スル者ナリ 袋獸屬 此屬ハ尾太クシテ小キ鱗ヲ蒙レリ此ノ尾ヲ以テ樹枝ニ倒懸シ果實或ハ小動物を食フ其ノ足ノ構造ハ握ルヘキモノニシテ極滑ナル者ト雖モ能クヲ握ル |
|||
| また, 14歳の貞治が認めた『明治廿三年ノ新正ヲ賀ス』も, 当時の貞治の性格や未来への力強い意欲が窺える興味深い資料である. |
 14歳時の作文『明治廿三年ノ新正ヲ賀ス』(1890) |
| 光陰矢ノ如ク明治廿二年旣ニ去リ鳳歴茲ニ再ヒ端ヲ開キ明治廿三年ノ春トハナレリ 昨年内ニ起コリシ出来事ヲ回想スレハ恍惚トシテ昨日ノ夢ノ如シ 嗚呼昨年ハ實ニ多忙ノ年ニテアリシ其社會ニ起リシ事ハ有形無形頗ル夛シ 吾人ハ先指ヲ憲法發布ニ屈セントス 憲法旣ニ定マリ我國立憲政體ノ基礎始メテ立チ確トシテ又動カスベカラズ |
|||
| ややペダンティックな趣を否めない表現であるが, いずれは国を背負って立つことを自覚する若々しい気概が感じられる論説であり, 読んでいて微笑ましい. 中学校で用いられたテキストは英語による原書であった. 当時の様子を後年の貞治が記した |
| 高木貞治『中学時代のこと』/ 学校図書株式会社『学図』第1巻第3号 (1952年10月号), pp.2-4. | |||
| の自筆原稿が「記念室」に展示されている. |
 後年の貞治による回想文『中学時代のこと』(1890) |
| 最近, 或る機會に, 人から聞かれて, 幼年時代の思い出話をしたときに感じたことは, 老来の健忘, 驚くべき記憶の不確なことであつた. その覚束ない記憶を辿つて, 中学時代の事を少しばかり書いて見よう. (中略) あの頃, 日本語の教科書というものは殆ど無かつたのであろう. 吾々の使つたのは, 全部が, いわゆる「原書」であつた. |
|||
| 原書によるテキストは, 特に初級生や2年生には難しかったため, 教師が大意を講義して生徒がそれを筆記し, 問題を解く際にだけテキストを参照していたようである. この時代における貞治の授業ノート (数学) を見てみよう. 「展示室」にあるのは「立体幾何」のノートである. 青で印刷された縦書き用の罫紙に, 一字一句, 丁寧に清書されている. |
 「立体幾何学」の授業ノートと解説パネル |
| 前出の『中学時代のこと』によれば,「(テキストは)トードハンターの小代数, ウィルソンの幾何学を使つた.」とある. 「立体幾何」の授業におけるテキストは, 英国の数学者ウィルソン (James Wilson, 1836-1931) の |
| [Wilson] J.Wilson "Solid Geometry and Conic Sections New Editions" Macmillan, 1882, 全156頁. | |||
| であろう. このテキストでは, 基本的な立体図形や円錐曲線の性質が詳細に解説されているが, 中には, 球面三角形の面積 (p.66) や正多面体におけるポアンカレの双対定理に関する問題 (p.70) , 射影平面上の完全四角形と調和点列 (pp.85-88) など, 現在の中学や高校では扱われない題材も含まれている. ところで, 上掲のノート (展示箇所) の内容は基礎的なもので |
| 定義二十七 正圓錐体ハ直角三角形カ其直角ヲ作ル 一辺ノ周リニ廻轉シテ生スル体ナリ ABC ヲ直角三角形トシBヲ其直角トス 今此三角形ヲ AB 辺ヲ周リテ廻轉セシムレバ AC ノ痕跡ハ圓錐面ヲナシ BC ハ圓ヲ作ル 此圓ヲ圓錐体ノ底ト云フ |
|||
| と, 貞治自身の翻訳で記されている. これは, [Wilson] pp.43-44 における |
| Def. 27. A right circular cone is the solid produced by the revolution of a right-angled triangle round one of the sides containing the right angle. Thus let ABC be a triangle right-angled at B, and let it revolve round AB. Then AC will trace out a conical surface. BC will trace out a circle, which is called the base of the cone. |
|||
| に該当する. 一方, 英国の数学者トドハンター (Isaac Todhunter, 1820-1884) の代数のテキストは, 当時の最新版としては, |
| [Todhunter1] I.Todhunter "Algebra for beginners with numerous examples New edition" Macmillan, 1887, 全328頁. | |||
| [Todhunter2] I.Todhunter "Algebra for the Use of Colleges and Schools New edition" Macmillan, 1877, 全608頁. | |||
| の二種が存在した. 「展示室」にはこの時代のノートが展示されていないため,「小代数」が何れのテキストを指すものかは判断できない. 仮に上掲書の何れか一方が該当するならば, 当時の中学で扱う内容に鑑みて [Todhunter1] と推察されるが, このテキストには, 基礎的な問題のみならず, 現在で言えば, いわゆる難関大学を目指す高校生 (受験生) にも通用し得るような高度な演習問題が散在している. 一方, [Todhunter2] の前半部も現在の中学校や高校で扱われる内容であるから, これが授業のテキストとして用いられた可能性も皆無とは言えない. しかし, その後半部になると, 冪級数展開 (pp.335-343) や連分数展開 (pp.375-387, pp.514-531), 超幾何級数 (pp.511-514) およびその連分数展開への応用 (pp.527-529) など, 現在の大学レヴェルの話題が含まれている. ウィルソンおよびトドハンターの何れのテキストも, 演習問題が豊富で興味深い内容である. しかし, 中学校の授業で扱われるものとしては, 問題の量の膨大さとレヴェルの高さに驚かされるのである. 何れも巻末に演習問題の解が付されてあるが, あくまでも最終解 (略解) のみであり, 末尾にある「他の出版物を宣伝する広告」を見ると, これらの詳細な解答集は別売にされていたことが分かる. ところで,「展示室」には,「14歳の時のもの」と解説パネルに記された (1889年11月27日の日付がある) ノートも展示されている. |
 交代式に関するノート (1889) |
| ところが, この内容はトドハンターによる上掲のテキストには存在しない. ノートの「第二 ―― 交代式」の項の冒頭部には, |
| 抑 交代式ナル名稱ハ髙等代數學ニ於テハ旣ニ久シク用ヒ来レル者ナレド, 余輩ハ未タ嘗テ此名稱ヲ初等代數學教科書中ニ見タルコトナシ. 然レドモ, 一通リ, 交代式ノ何タルヲ知ルコトハ, 甚タ容易ニシテ且對稱式トハ最も親密ナル関係ヲ有スルモノナレバ, 旣ニ對稱式ヲ論シタル以上ハ是非トモ交代式ノ何タルヲ詳ニセザルベカラザルナリ. |
|||
| のような, やや大袈裟な前置きがある. ここに記された「余輩」が貞治自身を指すものとすれば, より程度の高い他のテキストを繙いた貞治が独自に作成したノートということになるが, 次頁の中ほどには「能ク交代式ノ何タルヲ飮込ミタル讀者ハ容易ニ左ノ定理ヲ發見スルコトヲ得ベシ.」なる一文がある. これにより, これが貞治以外の「読者」を想定したノートなのか何かの原書を正直に翻訳したノートなのか, 判然としなくなるのである. 因みに, 現在の岐阜県立岐阜高等学校に保存されている貞治の成績表 (4年級時) によれば, 漢文97 英語95 代数100 幾何93 化学70 体操77 …… で, 平均86, 席次は22名中1位であったという. |
| 一色学校と岐阜県第一中学校を何れも首席で卒業した貞治は, 1891年, 16歳になる年に, 第三高等中学校 (後の旧制第三高等学校, 京都大学の前身) に入学した. 中学からの推薦により, 無試験であったという. 貞治は, 初めて親元を離れ, 京都での下宿生活を始めたのである. 第三高等中学校時代も, どの科目も熱心に聴講した様子が窺える. 授業のノートは, 青で印刷された縦書き用の罫紙に図や解説が丹念に書き綴られており, 何れも極めて読みやすい. テキストはやはり原書であったらしく, 貞治のノートにも, 本文は縦書きであるが随所に横文字が見られる. 例えば, 細胞, 組織, 果実などが項目別に記載された「植物学」の授業ノートには,「凡テ, 次第ニ生長スル維管束ヲ開出又ハ無限維管束 Open or Indefinite Bundle ト云ヒ, 次第ニ生長セサル者ヲ封鎖又は有限維管束 Closed or Definite ――ト云フ」とある. また,「農学」の授業ノートには, 牛一頭の全体像が描かれ, 番号を附された各部位の名称が整然と記載されている. 事物をつぶさに観察し, それを精確に描く貞治の観察と画力とに感嘆させられるのである. |
 |
 第三高等中学校時代の「植物学」(上) と「農学」(下) のノート |
| 貞治が数学者を志すようになったのは, この第三高等中学校時代であった. 当時の三高には, 帝国大学を卒業して後に京都帝国大学教授となる新進気鋭の数学者河合十太郎 (1965-1945) がいた. 貞治と同様, 貞治と同期の吉江琢兒 (1874-1947), 一級上の林鶴一 (1873-1935) も, 河合の薫陶を受けて数学者を目指すことになるのである. 河合は, ドイツ留学時代にクライン (Felix Christian Klein, 1849-1925) とヴェーバー (Heinrich Martin Weber, 1842-1913) に学んだ関数論の専門家で, |
| [百年史上]『日本の数学100年史 上』岩波書店, 1983, 全337頁. | |||
| によれば,「よく整理された講義をし, (上掲の3名を含む) これらの俊秀に数学への志向を植えつけた.」(p.231) という . 「展示室」には, 河合十太郎の講義を纏めたノートが展示されている. 一つは, 解説パネルに「随感録」と表示された縦書きのノートで,「第三高等中学校当時のものと思われる.」とある. |
 「随感録」と解説パネルにある「代数学」のノート |
| ノートを見ると,「一次方程式ヨリ生スル不合理ノ商」なるタイトルの次に「英国, あいざっくとゞはんたー」なる記述がある. 実際, その内容 |
| 凡テ一元一次方程式ハ\(\,ax\!=\!b\,\)ナル形に直スコトヲ得ベシ, 此方程式ヨリ\(\,\displaystyle{x\!=\!\frac{b}{\!\:a\!\:}}\,\)ヲ得. 偖, 若\(\,a\!=\!0\,\)ナルトキハ\(\,x\,\)ノ價ハ\(\,\displaystyle{\frac{b}{\!\:0\!\:}}\,\)ナル形ヲナス, 此場合ニ於テハ\(\,x\,\)ニ如何ナル價ヲ與フルモ, 此方程式ニ適合スベカラズ, 其故ハ\(\,x\,\)ニ如何ナル價ヲ附スルトモ, \(ax\!=\!0\,\)トナルヲ以テ, \(0\!=\!b\,\)トナリ, 即チ不合理ナルヲ以テナリ. |
|||
| は, [Todhunter2] p.117 における |
| Every equation of the first degree with one unknownquantity may be reduced
to the form \(ax\!=\!b\,\). Now from this we obtain \(\,\displaystyle{x\!=\!\frac{b}{\!\:a\!\:}}\). If \(\,a\!=\!0\,\)the value of takes the form\(\,\displaystyle{\frac{b}{\!\:0\!\:}}\,\); in this case no finite value of\(\,x\,\)can satisfy the equation, for whatever finite value be assigned to\(\,x\), since\(\,ax\!=\!0\), we have\(\,0\!=\!b\), which is impossible. |
|||
| の忠実な翻訳である. もう一つは横書きの英文によるノートで, 解説パネルには, "Elementary Trigonometry, 1892年",「河合十太郎教授の講義を, 高木博士がまとめたノート」とある. |
 河合十太郎「初等三角法」講義のノート (1892) |
| ここには二種類の定理が記されている. 一つは,「三角形ABCの垂心をP, 外心をOとして, 辺BC の中点を A'とするとき, AP=2OA'.」であり (下図参照), 簡明な証明が付されている. |
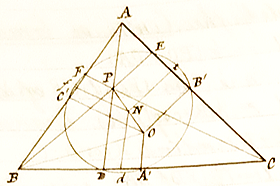 貞治が描いた九点円 (上掲の写真の一部を拡大したもの) |
| 他の一つは, フォイエルバッハの定理の一部「三角形ABCの九点円は内接円に接する」であり, その証明が「この二つの円の中心間の距離がそれらの半径の差に等しい」ことをもって示されている. 貞治のノートの表紙には河合十太郎とトドハンターの名が記載されているが, 現在の我々が目にすることができるトドハンターの著書に "Elementary Trigonometry" なるタイトルは見当たらない. トドハンターによる三角法のテキストは, 当時の最新版としては, |
| [Todhunter3] I.Todhunter "Torigonometry for Beginners with numerous examples" Macmillan, 1866, 全228頁. | |||
| [Todhunter4] I.Todhunter "Plane trigonometry for the use of colleges and schools with numerous examples New Edition" Macmillan, 1890, 全341頁. | |||
| の二種であった. 後者には九点円に関する記述が見られる (pp.276-278) が, 貞治が記したような三角法による詳細な証明は記載されていない. ところで, 澤山勇三郎 (1860-1936) は, |
| [澤山] 森本清吾編『澤山勇三郎全集』岩波書店, 1938, 全310頁. | |||
| においてフォイエルバッハの定理に24通りの証明を与えている (pp.3-25, pp.109-167) が, その中にも貞治と同一の証明法は記載されていない. 最も近い手法を強いて挙げるならば, 第22証明 ([澤山] pp.165-167) であろうか. しかし, これらの証明が『東京數學物理學會記事』(第2期, 1901-1918) に掲載されたのは, 上掲の講義ノートが作られてから10年以上も経過した後のことである. 後年の貞治は, 既に証明された定理であっても貞治自身の創意工夫を加えた手法で著作に纏めることがあった. このノートにもその片鱗が表れているように思う. |
| 第三中学高等学校を優秀な成績で卒業した貞治は, 1894年, 19歳で帝国大学理科大学 (現在の東京大学理学部) に (吉江琢兒, 林鶴一と共に) 入学した. この時も無試験であったという. 当時, 帝大数学科における日本人教授は菊池大麓 (1855-1917) と藤澤利喜太郎 (1861-1933) の二人であった. 菊池はイギリス留学を経て22歳で教授に就任し, そのときの学生であった藤澤利喜太郎がドイツ留学を経た後に教授として加わったのである. |
 菊池大麓 (1855-1917) |
 藤沢利喜太郎 (1861-1933) |
| 貞治の帝大時代の状況を, 前出の [本田] および [百年史上] に加え, 貞治自身が学生の頃を回想した講演録『回顧と展望』(東京帝国大学理学部数学談話会, 1940) を援用して概観することにしよう. この時代の貞治自身のノートの存在は確認できないが, 吉江琢兒の当時のノートによれば, 藤澤利喜太郎が担当した解析関係の内容は次のようなものであった ([百年史上] pp.165-166). 【第1,2年】微分積分学 微分法:実数, 極限, \(\varepsilon\)-\(\delta\,\)流の連続関数, テーラー展開, 偏微分, 全微分, 微分幾何初歩, 等. 積分法:定積分, 特異積分, 留数計算, ガンマ関数, ディリクレ積分, ベルヌーイ数, 等. 微分方程式:一階常微分方程式, 特異解, 定係数線形常微分方程式, 全微分方程式, 等. フーリエ展開:ディリクレ条件, フーリエ積分, 変分法初歩, 極小曲面. ルジャンドル微分方程式:ベッセル方程式, 超幾何級数, 全微分方程式の積分条件. 偏微分方程式:一階の場合, シャルピの方法, 二階の場合, 等. 【第2年】楕円関数論 楕円積分, ヤコービの楕円関数, 乗法理論, テータ関数, 変換公式と楕円関数の表示, 等. 【第3年】一般関数論 複素積分とコーシーの定理, 留数計算, 解析接続, アーベル積分とアーベル関数, 代数関数とリーマン面, 等. 現在の大学におけるカリキュラムと比較すると, 講義の順序や内容の点において, 雑多で詰め込み主義的な印象を受ける. また,『回顧と展望』には, 次のような述懐がある. |
| 當時何を敎はつたか, 古い記憶を辿つて見ると, 先づ微分積分それから解析幾何學. これは當然だが, 次で二年になると, Durege の楕圓函數論といふものをやつたものである. これは古い本だから, 諸君は知らないだらうが, まあヤコービの楕圓函數論を書いたもの, つまり Fundamenta Nova の平易な解說といつたものである. 函數論の出來る前の楕圓函數論で, 随分時代離れのものだが, 多分これは, 私の想像なんだけれども, ずつと明治の初期に, ケンブリッヂ邊りから, さういふシステムが輸入されたのではないか ―― と思はれる. それから, サルモンの代數曲線論, 例の略記法か何かで, 吾々はそれが射影幾何學であることを知らずに習つた (後略) |
|||
| ここに現れる「Durege の楕圓函數論」は, デュレージュ (Heinrich Durège, 1821-1893) の |
| [Durège] H.Durège"Theorie der Elliptischen Functionen Versuch Einer Elementaren Darstellung, Dritte auflage" B.G.Teubner, 1878, 全390頁. | |||
| であると思われる. [百年史上] p.170 に掲載されている1897年当時の東京帝大数学科の蔵書一覧の中に, 楕円関数やアーベル関数論についての著書として "H.Durège
(1878)" なる記載があるからである. これは, 楕円関数を第一種楕円積分の逆関数と看做したヤコビ (Carl Gustav Jacob Jacobi, 1804-1851) の "Fundamenta Nova" 即ち |
| [Jacobi] C.G.J.Jacobi "Fundamenta nova theoriae functionum ellipticarum" Sumtibus Fratrum, 1829, 全191頁. | |||
| をもとに, 楕円関数の構成とその応用を詳細に解説したものである. 貞治は, 後に複素関数論が発展して楕円関数の二重周期性や解析性から楕円関数を再構成したヴァイエルシュトラス (Karl Weierstraß, 1815-1897) の手法が一般的になったことに鑑みて, 前者を「時代離れ」と評したのであろう. ところで, 講演録『回顧と展望』は, 後に『近世數學史談』に収録されることになったものである. 『近世數學史談』には, [初版] (共立社書店, 1933), [第2版] (河出書房, 1942年), [第3版] (共立出版, 1970年), [岩波文庫版] (岩波書店, 1995年) が存在するほか,『數學雜談』との [合本版] (共立出版, 1946年, 1996年) も存在する. [第3版] 以降は, [第2版] の内容を現代仮名遣いに改めただけであり, 内容としての差異はない. 実は, 上掲書の他にも (一般にはほとんど知られていないが) 講演の速記録を活字化した |
| [速記版] 高木貞治『回顧と展望』考へ方研究社『高數硏究』第5卷第4號 (1941年1月), pp.1-6. | |||
| が存在し, ここには, 上掲書とは異なる表現や上掲書では削除されている箇所が含まれている. 以下, 特に必要がない場合 (断りなく『回顧と展望』を引用する場合) は, [第2版] を用いることとする. |
 『近世數學史談 2版』 (河出書房, 1942) |
| さて, 貞治の言う「ケンブリッヂ邊りから」云々は, 日本人初のケンブリッジ大学の卒業生であった菊池大麓の影響を示唆したものであろう. イギリスで欧米の自由主義的ないし進歩主義的な思想に接した菊池は, 早期のうちに日本を欧米先進国の水準にまで高めようと考えたものと思われる. その菊池大麓は幾何の担当であった. 第一年および第二年では平面と立体の幾何が扱われたという. 小倉金之助 (1885-1962) は, |
| [小倉]『小倉金之助全集第2巻』勁草書房, 1973, 全402頁. | |||
| において, 帝国大学数学科の最初 (第一期生, 1894年) の卒業生であった高橋豊夫 (1861-1944) に当時の教科書に関して尋ねている. それによれば,「平面解析幾何は教科書を用いなかったが, それはサーモンの『円錐曲線』のような講義であった」という
(pp.52-53). 高橋の十数年後に入学した貞治は, 明確に「サルモンの代數曲線論」と述べている. これは, サーモン (George Salmon, 1819-1904) の最新版のテキスト |
| [Salmon1] G.Salmon "A Treatise on Conic Sections 6th edition" Longman, 1879, 全399頁. | |||
| またはその続編に該当する |
| [Salmon2] G.Salmon "A treatise on the higher plane curves: intended as a sequel to A treatise on conic sections 3rd edition" Hodges, Foster&Figgis, 1879, 全389頁. | |||
| であろう. [Salmon1] は, 直交座標, 極座標, 行列式による (直線や曲線の) 表記法および射影幾何の手法を用いて, 円錐曲線が有する多くの性質およびその応用が詳細に解説されるテキストである. [Salmon2] は, 斉次座標, 代数曲線の一般的性質 (方程式の項数, 交点と接線, 曲線の描画, 極など), 包絡線, 三次曲線, 四次, 超越曲線, 変換論 (線型変換, 射影変換, クレモナ変換など) が扱われるテキストである. 貞治の言う「略記法」は現在では耳慣れない用語であるが, [速記版] における該当箇所を見ると「サルモンのアブリツジト・ノーテーションを射影幾何とは知らずに習つた」とある. 恐らく "abridged notation" を指すのであろう. この用語の初出となる [Salmon1] の "CHAPTER IV" (p.53) には, |
| Let us call \[x\cos\alpha+y\sin\alpha-p,\:\alpha\,;\:\:x\cos\beta+y\sin\beta-p,\:\beta.\]Then the theorem just stated may be more briefly expressed ; the equation \(\alpha-k\beta=0\) denotes a line passing through the intersection of the two lines denoted by \(\alpha=0,\:\beta=0\). We shall for brevity call these the lines \(\alpha,\,\beta,\) and their point of intersection the point \(\alpha\beta\). | |||
| とある. ヘッセの標準形を用いた直線束を\(\,\alpha-k\beta=0\,\)と表記するというものである. この記法により, "CHAPTER IX" (pp.201-202) では,「四辺形を作る4直線\(\,\alpha,\beta,\gamma,\delta\,\)に対し, \(\alpha\gamma=k\!\:\!\:\beta\!\:\delta\,\)は, この四辺形の4頂点を通る二次曲線を表す.」なる定理が示される. この表記を用いて初等幾何学における種々の定理を示す手法はなかなか鮮やかであり, 興味深いものがある. 菊池による幾何では, 2次曲線や2次曲面を含めて射影幾何学的に扱われ, 解析幾何ではなかったという. 第2年における平面代数曲線論の講義では, 特異点やプリュッカーの公式, 3次曲線 (楕円曲線) の理論 (不変量など) が扱われたようである ([百年史上] p.166). |
| 『回顧と展望』において, 貞治による学生時代の回顧は次のように続く. |
| 藤澤先生はベルリンでクロネッカーの講義を聽かれたらしいのであつて, 代數を大學へ入れなくてはならぬといふことを絕えず言つてゐられたのであるが,
當時日本では, 代數は中學校でもう卒業してしまつたもののやうに考へられてゐた. そこでその後セミナリが出來てからは, さういふ處で頻りに代數の問題を與へられた. 當時代數といへばセレーの「高等代數」で, それによつて, 私は, アーベル方程式を讀めと言はれ, そこで謂はゆる高等代數の洗禮を受けたわけである. しかし, その當時, 已に書棚の隅つこに, ウエーバーの「代數學」の第1卷が來てゐたので, それを探し出して, ガロアの理論に接したのだが, それが本當に分つたのだかどうだか, その後, 段々いろいろ新しいものが來るやうになつて, ウエーバー第2卷も軈て來た. |
|||
| [本田] によれば,「藤沢はドイツで, 学問としての数学を, 本格的に学び, また '研究する' ということも学んできた」といい,「彼が, 数学のセンスを十分もっていたことは, 1900年のヒルベルトの有名なパリ講演をきいて, それを日本に紹介している文章が,
かなり的確にその内容を把握していることからも, よく了解される.」という. 貞治の言う「セミナリ」とは, 第3年の随意科目として藤澤の創設により1893年頃から制度化された「数学研究」([百年史上] p.215) を指すのであろう . 学生ごとに個別に異なる課題が与えられ, 一定期間の後にレポートを提出するものであったという. 藤澤が貞治に「アーベル方程式」を課した経緯は不明であるが, 結果として, これが貞治の数学者としての方向性を決定づけるものとなった. 以下, これに関して少し詳しく述べることにする. 1896年から1900年にかけての5年間に,『藤澤敎授セミナリー演習錄』全5巻が東京数学物理学会から刊行された. 貞治のレポート『あーべる方程式ニツキテ』は, その第2巻 (1897) に収録されている. ここでは, |
| [科学技術史]『日本科学技術史大系 第12巻』第一法規出版, 1969, 全641頁. | |||
| に掲載された記事を援用して貞治のレポートを概観してみよう. 前掲の『演習録』第一巻の緒言において,「セミナリ」および『演習録』の意図を, 藤澤利喜太郎は次のように述べている ([科学技術史] p.108). |
| 余ガ「セミナリー」に於テハ學生諸氏ヲシテ或ル時ハ數學上特別ノ事項ニ就キ調査講窮セシメ或ル時は著名ナル數學大家ノ論文ヲ講讀論評セシメ又或ル時ハ恰好ナル問題ニ就キ自家ノ硏窮ヲ爲サシメ演習ノ方法ハ一ツニ時宜ニ任カス (中略) 其中ニハ間々貴重ナル材料ナニキシモアラズシテ此儘之ヲ捨ツルノ何ントナク物惜シキ心地セラルヽモノカラニ其中に就キ世ニ裨益スルトコロアラント思ハルヽ二三ノ篇ヲ撰ビ題シテ「セミナリー」演習錄ト名ヅケ東京數學物理學界ニ請ヒ同會ノ出版物トシテ出版スルコトヽセリ |
|||
| 藤澤が貞治に与えた課題は,「アーベル方程式を讀め」であった. 留学中に藤澤自身が目の当たりにした現代数学の一端を貞治に覗かせようとしたものと思われる. 貞治の『あーべる方程式ニツキテ』は, 方程式の代数的可解性に関して報告するものである. その序文には, ガウスによる二項方程式の解法からアーベルが根の間の特殊な関係を見出したこと, ガロアがその理論的裏づけを成し (リューヴィルが世に知らしめ) たことが後にエルミート (Charles Hermite, 1822-1901) やクロネッカー (Leopold Kronecker, 1823-1891) 達の研究起点となったこと書かれている ([科学技術史] p.109). 興味深いことは, 貞治のレポートが, ガウス (Carl Friedrich Gauß, 1777-1855) からアーベル (Niels Henrik Abel, 1802-1829) やガロア (Évariste Galois, 1811-1832) に至る代数的可解方程式研究に関する客観的な報告に留まらず, 最新の代数学の理論の見地からこれらを捉え直そうとする意識が見られることである. 序文は次のように結ばれる. |
| コヽニ叙述セントスルハあーべる方程式ノ解法ニ止マル 而シテコノ叙述ニ於テ余輩ハあーべるノ跡ヲ追ハンヨリハ寧ロ最モ斬新ナル見地ヨリ翻テコノ問題ヲ考察セント欲スルモノナリ. コノ叙述ヲナスニ當リ余輩ハせれー, じょるだんねっとー及ビうぇーべる等ノ書★而モ特ニコノ最後ノオーソリチーニ負フ所甚ダ多カリシコトヲ告白セザルベカラズ. |
|||
| [百年史上] pp.168-169 に記載された1897年当時の東京帝大の蔵書一覧から判断すると,『回顧と展望』で挙げられた「高等代數」とは, セレー (Joseph-Alfred Serret, 1819-1885) による |
| [Serret1] J.Serret "Cours d'algèbre supérieure I, 4ème édition" Gauthier-Villars, 1877, 全647頁. | |||
| [Serret2] J.Serret "Cours d'algèbre supérieure II, 4ème édition" Gauthier-Villars, 1879, 全694頁. | |||
| であり,「代數學」とは, ヴェーバー (前出, §1-4) による |
| [Weber1] H.M.Weber "Lehrbuch der Algebra I" F. Vieweg und sohn, 1895, 全653頁. | |||
| であろう. 『回顧と展望』の [速記版] には, |
| セレーの高等代數といふ本がありますが, それが唯一つのもので, それによつて僕にアーベルの方程式をやれといはれました. そんなことで所謂高等代數の洗禮を受けた. その時分, 私は圖書室の書棚を捜すと, 書棚には既にウェーバーの代數第一卷が來て居りそれを捜し出して讀んだのですけれども, 本當には判らなかつたのです. | |||
| という記載がある. 前掲の引用部では「本當に分つたのだかどうだか」であった箇所が, 上掲の引用部では「本當には判らなかつた」となっている. 数学に対して真摯に向き合い, 知ったかぶりをしたり誤魔化したりしない貞治の誠実な人柄がここに垣間見えるであろう. |
 J.A.セレー『高等代数学教程』(1879) |
 H.M.ヴェーバー『代数学教程』(1895) |
| 『あーべる方程式ニツキテ』には, 上掲書 [Serret2], [Werber1] に加え, ジョルダン (Camille Jordan, 1838-1922) の |
| [Jordan] C.Jordan "Traité des substitutions et des équations algébriques" Gauthier-Villars, 1870, 全667頁. | |||
| および, ネットー (Eugen Netto, 1846-1919) の |
| [Netto1] E.Netto "The theory of substitutions and its application to algebra" Ann Arbor, Mich., 1892, 全301頁. | |||
| の4書が参考文献 (上記引用部における★) として掲げられている. なお, [Netto1] は |
| [Netto2] E.Netto "Substitutionentheorie und ihre anwendungen auf die algebra" B.G.Teubner, 1882, 全291頁. | |||
| のコール (Frank Cole, 1861-1926) による英訳版であるが, 独語版に対して内容の取捨および各章の配置に変更が見られる. [百年史上] pp.168-169 における当時の数学科の蔵書一覧には, [Jordan] は記載があるが [Netto1] については記載がない. 無論, [百年史上] に全ての蔵書が記載されているわけではないであろうから, [Netto1] が数学科の図書室に存在しなかったとは断定できない. [Weber1] を読んでみると, [Jordan] と [Netto2] の書名が p.481 の脚注に現れる. 貞治は恐らく, ヴェーバーを読む中でこれらの書物の存在を知ったものと思われる. |
 C.ジョルダン『置換論と代数方程式』(1870) |
 E.ネットー『置換論』(1892) |
| 余談であるが, ヴェーバーの『代数学教程』は, 現在では, |
| [Weber2] H.M.Weber "Lehrbuch der Algebra II" F. Vieweg und sohn, 1896, 全784頁. | |||
| [Weber3] H.M.Weber "Lehrbuch der Algebra, III" F. Vieweg und sohn, 1898, 全726頁. | |||
| を含めた三部作と看做されているが, [Werber3] は, 先に出版された『楕円関数と代数的数』即ち |
| [Weber4] H.M.Weber "Elliptische functionen und algebraische zahlen" F. Vieweg und sohn, 1891, 全504頁. | |||
| の改訂増補版であり, 後から追加されたものである. 実際, [Weber1] および [Weber2] の原書の表紙 (上掲) を見ると "IN ZWEI BÄNDEN" なる記載がある ([Weber3] の表紙にこの記載はない). 貞治が「第2巻も軈て來た」と述べている点に鑑みると,『あーべる方程式ニツキテ』の執筆時点において, 貞治は [Weber2] を読んでいなかった可能性がある (但し, 前述した東京帝大の蔵書一覧には [Weber2] の記載がある). それ以前に出版されていた [Weber4] についてはどうか. この書物については蔵書一覧に記載はない. ところで, 上掲の代数学書に関しては, 今現在に至るまで邦訳版が存在しない. 原書 (英語, 仏語, 独語) である点, 用語や表記法が現代のものとは異なる点, 微に入り細に亘る懇切丁寧な解説が頁数を膨大にさせている点などが, これらの書をかなり読みづらいものにさせている. 貞治が独習したこれらの専門書の内容を少し覗いてみよう. まず, [Serret1] では, 連分数の一般論, 代数学の基本定理, 連立方程式に関する諸定理, 円分方程式と原始\(\,n\,\)乗根, 代数方程式の解に関する諸定理とその数値的解法, 解と係数の関係, 対称式の基本定理, 有理関数分解, 連立代数方程式における消去理論などが解説される. 次に, [Serret2] では, 合同式の一般論, 平方剰余の相互法則, 原始根とその応用, 素数を法とする多項式の分解および既約性, 素数を含む範囲に関するチェビシェフの不等式, 対称群や共役類に関する一般論, 三次および四次方程式の代数的解法, 円分方程式に関する諸定理, 代数方程式の代数的可解性などが解説される. これらの話題の多くは, 後に『代数学講義』や『初等整数論講義』の中に纏められることになるものである. その中で, 貞治の『あーべる方程式ニツキテ』と緊密な関連性をもつ箇所は [Serret2] の終章である. そこには, ガロアによるメモ『方程式の代数的可解条件に関する覚書』即ち |
| [Galois1] E.Galois "Mémoire sur les conditions de résolubilité des équations par radicaux" 1831/1846. | |||
| [Galois2] E.Galois "Des équations primitives qui sont solubles par radicaux, second mémoire" 1830/1846. | |||
| の解説 ([Serret2] pp.637-667) と, クロネッカー (前出) による論文『代数的に可解な方程式について』即ち |
| [Kronecker1] L.Kronecker "Über die algebraisch auflösbaren Gleichungen" Akademie der Wissenschaften zu Berlin., 1853, pp.365–374. | |||
| の全文の (セレー自身による解説や言及をもたない) 独語訳がある. そこにおけるガロアの主旨は「代数的に可解なる条件は, 多項式の任意の根が他の根の有理関数として表せること」であり, クロネッカーの主旨は 「\(\mathbb{Z}\,\)係数アーベル方程式の根は,1の冪乗根の\(\,\mathbb{Z}\,\)係数有理関数として表せること」であった. また, [Werber1] では, 整関数および有理関数の一般論, 行列の一般論とその応用, 対称式の基本定理, 代数学の基本定理, 線形変換, シュトゥルムおよびブーダン-フーリエの定理, 数値方程式における近似法, 連分数とその応用, 円分方程式と原始合同根, 平方剰余の相互法則, 代数体とガロア群, 置換群と巡回方程式, ラグランジュの分解式, 円分方程式とガウス和, ガウス整数と素因子分解, 方程式の代数的可解性の条件などが解説されている. 上掲書における内容は, 現代では用いられない記号や用語が数多く見られ, 読みづらく理解しがたい箇所が少なくない. すると,『あーべる方程式ニツキテ』における「あーべる方程式」の意味するところも疑わしくなるのであるが, [Werber1] の第15節を見ると, それまでに述べてきた巡回方程式に加え, 次のような記述が現れる. |
| Eine irreducible Gleichung \(\varphi(x)\!=\!0\) mit commutativ er Gruppe ist eine Abel'sche Gleichung. | |||
| 即ち, ヴェーバーはガロア群が可換群となる既約方程式も含めてアーベル方程式と称していることが分かる (p.535). これは, 現今の定義と一致するものであるから,
貞治もこの意味で「あーべる方程式」を用いていたと考えてよいであろう. 貞治にとっての肝要部分は, 代数的可解方程式に関する部分であった. 貞治は, 上掲書を繙くことにより, 中学や高校で習ってきたような数式計算を中心とする初等代数ではなく, それらを含有する代数的構造を解明する「高等代數」の「洗禮を受けた」わけである. [Jordan] では, 合同式や平方剰余に触れた後, 直ちに置換の一般論に移り, 一般方程式論へと続く. 内容は [Werber1] よりもやや進んでおり, \(n\,(\geq\!5)\,\)次方程式の代数的非可解性に留まらず, 五次方程式の超越的解法が紹介されている (pp.372-375). 五次モジュラー方程式を用いるエルミート (前出) の手法と, ヤコビの楕円関数を用いるクロネッカーおよびブリオッシ (Francesco Brioschi, 1824-1897) の手法が比較でき, 大変に興味深い. また, [Netto] では, 前半部は, 冪和や判別式を含む対称式の一般論から始まり, \(p^{\!\:k}\,\)次対称群, 群作用, メタ巡回群など, 方程式の代数的可解性を論じるのに必要な概念が解説される. 後半部は, \(n\,(\leq\!4)\,\)次方程式, アーベル方程式, ガロア方程式, 素数冪次方程式の代数的可解性を中心に解説される. |
| さて, 貞治による『あーべる方程式ニツキテ』を見てみよう. これは, 序文を除いて全13節で構成され, |
| 第一節 體 第二節 體ノ中ノ函數 第三節 代數體 第四節 正體トがろあノ分解式 第五節 がろあ群 第六節 群ノ移動性ト方程式ノ分解性トノ關係 第七節 群ニ關スル定理 第八節 根ノ有理式 第九節 分解式ノ簡約 第十節 あーべる方程式 第十一節 あーべる方程式ヲ循環方程式ニ歸セシメ得ベキコト 第十二節 循環方程式ノ解法 第十三節 結論 |
|||
| から成る67頁に及ぶレポートである. オリジナルの論文ではないが, ガロア理論をわが国に最初に紹介したレポートとして記憶されるべきものである. その肝要部分である第5節「がろあ群」の冒頭部を見てみよう. |
| \(\varOmega\,(\rho)\,\)ヲ\(\,\mu\,\)次ノ正體\(\,g\,(t)\!=\!0\,\)ヲ\(\,\rho\,\)ノ適合スル\(\,\mu\,\)次ノ旣約方程式\(\,\rho\,,\,\rho_{{}_{1}}\,,\,\cdots,\,\rho_{\mu-1}\,\)ヲ\(\,\rho\,\)ト共軛ナル數トス サスレハ正體ノ定義ニヨリテコレラノ共軛數ハ皆\(\,\varOmega\,(\rho)\,\)ニ屬スルカユヘニ\[\rho_{{}_{1}}\!=\!\theta_{{}_{1}}\!\:(\rho),\,\cdots,\, \rho_{\mu-1}\!=\!\theta_{\mu-1}(\rho)\]ト書くコトヲ得. コヽニ\(\,\theta_{{}_{1}}\,,\,\cdots,\,\theta_{\mu-1}\,\)ハ\(\,\varOmega\!\:\)ノ中ナル\(\,\mu\!-\!1\,\)次以下ノ整式ナリトス. サテ\(\,\omega\,\)ヲ\(\,\varOmega\!\:(\rho)\,\)ノ中ノ一數トセハコレト共軛ナル數ヲ次ノ如ク表ハスコトヲ得.\[\omega\!=\!\varphi\!\:(\rho),\,\omega_{{}_{1}}\!=\!\varphi\!\:(\rho_{{}_{1}}\!\:), \,\cdots,\,\omega_{\mu-1}\!=\!\varphi\!\:(\rho_{\mu-1})\] \(\varphi\,\)モ亦\(\,\varOmega\!\:\)ノ中ナル\(\,\mu\!-\!1\,\)次以下ノ整式ナリトス. 叉逆ニ\(\,\psi\,\)ヲ以テ\(\,\varOmega\!\:\)ノ中ノ有理函數ヲ表ハスモノトセハ\[\psi\!\:(\rho),\,\psi\!\:(\rho_{{}_{1}}\!\:),\,\cdots,\,\psi\!\:(\rho_{\mu-1})\]ハ共軛數ナルコトハ明カナリ. |
|||
| 上記における「正體」は聞き慣れない用語であるが, 前後の文脈から「正規拡大」を指すものと思われる. 以後, 先述したセレーのテキストにおけるガロアの主旨が解説されるのであるが, この節の叙述は, ヴェーバー [Weber1] の pp.467-478 に記載されている |
| §146. "Die Substitutionen eines Normalkörpers." (正規拡大の置換) §147. "Zusammensetzung der Substitutionen." (置換の構成) §148. "Permutationsgruppen." (置換群) §149. "Galois'sche Gruppe." (ガロア群) |
|||
| の翻訳と言ってよい. 一方, 群の (現代とは異なる) 定義を補足したり, 記号の書き換えや置換演算に関する説明の割愛したり, 叙述の方法や順序を改良したりなど, 貞治自身による工夫も随所に施されている. この節の後半部では, 次のように要約される. |
| 今\(\,n\,\)個ノ根ノ有理式アランニコレラノ根ノ間ニ一ノ置換ヲ施コストキコノ有理式ハソノ値ヲ變セサルトキハコノ有理式ハコノ置換ヲ許スモノト做スシカスルトキハ \((\mathrm{I})\) \(F(x)\,\)ノ\(\,m\,\)個ノ根ノ間ニ成立スル所ノ\(\,\varOmega\!\:\)ノ中ノ有理的等式ニがろあ群ノ置換ヲ施コシテ得タル結果ハ仍ホ正當ノ等式タルヲ失ハス \((\mathrm{II})\) \(F(x)\,\)ノ\(\,m\,\)個ノ根ノ有理式ニシテがろあ群ノスヘテノ置換ヲ許スモノハ\(\,\varOmega\!\:\)ノ中ノ數ナリ. |
|||
| その後, それ以前に提示した4つの定理を根拠にこれらを証明し, この節は閉じられるのである. 先述した通り,『あーべる方程式ニツキテ』は貞治のオリジナルの論文ではない. このレポートは, 全編に亘って, [Werber1] における主要部分 |
| §139-§151. "Die Galois'sehe Theorie." (ガロア理論) §152-§158. "Anwendung der Permutationsgruppen auf Gleichungen." (置換群の方程式への応用) §159-§165. "Cyklisehe Gleichungen." (巡回方程式) |
|||
| を, 貞治自身が咀嚼吸収して纏めたものになっている. 貞治は, 上掲のテキストによって初めて「ガロア理論に接した」のであった. 自身は「本當に分つたのだかどうだか」あるいは「本當には判らなかつた」( [速記版]) と謙遜しているが, セレーやヴェーバーの著書を含め, 記号, 用語, 理論体系が不統一であった時代に, 上掲書のような大部の原書を読みこなす作業は尋常の努力では済まなかったはずである. 仮に, [Weber2] における群論関係の記述と, 私が学生時代に繙いたような代数学書 (例えば |
| [永田] 永田雅宜『可換体論 新版』裳華房, 1985, 全272頁. | |||
| など) のそれとを比較してみれば, 後者の方が遥かに簡単明瞭に書かれていることが理解されるであろう. 藤澤利喜太郎も貞治の非凡なる努力と才能を認めていたのであろう. 貞治のレポートを収録した (前掲の)『演習録』第二巻の緒言には, |
| 高木貞治氏ノ記述ニ係ハル第三ノ論文ハあーべる方程式ヲ論ズルモノニシテ論文ノ事實ヨリ推ストキハ第一冊掲載ノ諸論文ニ攝續スルモノナリ 而シテ高木氏ハ余ガ最初與ヘタル問題ヨリ一層一般ニ卽代數學最近發達ノ眞相ヨリシテあーべる方程式ヲ講窮セラレタルガ故ニ氏ノ論文ハ最モ新ラシキ代數學ノ要領ヲ得ルニ最モ便利ナルベシ. 此緒言ヲ終フルニ臨ミ特ニ一言シタキコトアリ, ソハ本冊の記述者タル三氏ガ何レモ余ガ與ヘタル問題ニ就キ叮嚀ニシテ周密ナル講窮ヲナシ能ク悟ル可キモ語ル可カラザル的ノ妙所ヲ觀破シ, 講窮ノ結果ヲ記述スルニ當リテハ其順序體裁ノ頗ル宜シキヲ得タルコトナリ. |
|||
| とあり, 貞治に対する惜しみない讃辞を与えている. ここで, 藤澤の言う「第一冊掲載ノ諸論文」とは, |
| ・奥田竹三郎『三次方程式四次方程式ノ解法及方程式ノ根ノ有理式ニ付テ』 ・渡辺庸『五次及五次以上ノ方程式ハ一般ニ係數ノ代數式ヲ以テ解クコト能ハザル事ノ證明』 ・吉田好九郎『一變數ヲ含ム有理整數代數函數ハ必ズ一次若シクハ二次ノ實因數ニ分括セラレ得ルト云フ定理ノがうすノ正確ナル證明』 |
|||
| を指し,「本冊ノ記述者タル三氏」とは, 貞治および前出の吉江琢兒と林鶴一を指す. なお,『演習録』第二巻に掲載された吉江と林のレポートは |
| ・吉江琢兒『似眞寫影』(等角写像) ・林鶴一『\(e\,\)及ビ\(\,\pi\,\)ノ超越ニ就テ』 |
|||
| であり,「第三ノ論文」が貞治の『あーべる方程式ニツキテ』であった ([科学技術史] p.93). ここで, 貞治が「軈て來た」と述べる「ウェーバーの第2卷」すなわち [Weber2] を見てみよう. まずは群論の基礎から始まる. 有限アーベル群の指標, 円分体のガロア群, アーベル方程式, 有限群におけるシローの定理, フロベニウス群など. 次に線形群論が続く. 行列論, 置換論, 有限群の不変式, ヒルベルトの基底定理, 直交群, 回転群, 対称群, 合同群など, 後の議論に必要な概念が準備される. 続いて応用理論が展開される. メタ巡回方程式, 代数的可解方程式に関するアーベルの定理, 三次および四次曲線論 (特に二重接線とガロア群), 五次方程式論 (特に正二十面体と超越的可解性) などが解説されるのである. その後, [Weber2] の主要部である代数的整数論に入る. 代数的整数に関する基本用語と性質, イデアルの素因子分解, 代数体の判別式および共軛差積, (凸体の格子点に関する) ミンコフスキの定理の代数体への応用, デデキントの判別定理, 二次体論および円分体論が展開される. 貞治は恐らくここで初めて代数的整数論に接したものと思われる. 無論, 講義による習得ではない. 自ら専門書を繙き, 精密に読み込み, 緻密によく考え, 根気強く独学を続けたことで, (当時における) 最先端の数学を咀嚼吸収していったのである. さて, [Weber2] 後半部, §179 (p.648) において, クロネッカーによる命題 |
| Alle im absoluten Rationalitätsbereich Abel'schen Zahlkörper sind Kreistheilungskörper | |||
| 即ち「\(\mathbb{Q}\,\)の任意の有限アーベル拡大は円分体である」が現れる. これは, 後年の貞治を第一級の数学者へと押し上げる契機となった重要な定理と言ってよい. この命題はやがて「クロネッカーの青春の夢」へと拡張され, それは貞治が後に類体論を構築することにより肯定的に解決されることになるからである. これについては次節で詳しく述べることにしよう. さて, 1897年に大学を卒業した貞治は, 大学院生として引き続き東京帝大に在籍した. 『回顧と展望』によれば, |
| その間にいろいろな本を讀んだのであるが, 指導者なしの亂讀で, 本當に讀んだと謂ふよりは, 圖書室にあるだけの本を見境ひもなく片つ端からひつ繰り返して見たといふ程のことであつた. | |||
| ということであり, 分野を限定することなく, 種々の数学書に目を通していたらしい. [百年史上] pp.170-171 には, 東京帝大数学科図書室に残されている図書貸出簿に関する記載がある. 大学3年間と大学院1年間の計4年間で, 貞治は延べ70冊の書物を借り出しているという. そこには, 前出 (§2-2.) のセレー, ヴェーバーのみならず, 以下の数学書が列挙されている. まず, ディリクレ (Peter Gustav Lejeune Dirichlet, 1805-1859) やデデキント (Richard Dedekind, 1831-1916) の『整数論講義』 |
| [Dirichlet] P.G.L.Dirichlet "Vorlesungen über Zahlentheorie" F. Vieweg und sohn, 1863, 全414頁. | |||
| [Dedekind] R.Dedekind "Vorlesungen über Zahlentheorie" F. Vieweg und sohn, 1871, 全497頁. | |||
| であり, 次にヒルベルト (David Hilbert, 1862-1943) の『整数論報告』 |
| [Hilbert 報文] D.Hilbert "Die Theorie der algebraischen Zahlkörper" Jahresb. Deutsch. Math. Verein Vol.4, 1897. | |||
| のほか,「楕円関数についての多くの古典」とある. これらに関して具体的な書名の記載はないが, 恐らく前出 (§2-1) のヤコビやデュレージュなどであろう. さらに, クライン (前出, §1-4) の二十面体論 |
| [Klein] F.C.Klein "Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade" B.G. Teubner, 1884, 全260頁. | |||
| や, ジョルダン (前出, §2-2) やピカール (Émile Picard, 1856-1941) の解析教程 |
| [Jordan1] C.Jordan "Cours d'analyse de l'École polytechnique I" Gauthier-Villars, 1893, 全613頁. | |||
| [Jordan2] C.Jordan "Cours d'analyse de l'École polytechnique II" Gauthier-Villars, 1893, 全627頁. | |||
| [Jordan3] C.Jordan "Cours d'analyse de l'École polytechnique III" Gauthier-Villars, 1893, 全542頁. | |||
| [Picard] E.Picard "Traité d'analyse" Gauthier-Villars, 1891, 全457頁. | |||
| などが挙げられている. |
| 貞治が大学院生として在籍した期間は一年足らずであった.「官費留学生」として「數學研窮ノタメ滿3ヶ年獨國留學ヲ命ズ」という辞令を受けたからである.
1898年6月末に大学院を退学した貞治は, 同年8月末にドイツへと向かったのであった. 引き続き『回顧と展望』から引用する. |
| 「洋行」は嬉しかつたが, (中略) 何分數學といへば獨逸, 獨逸といへばベルリンと言はれてゐた時代で, そこへ素養もなく, 自信もない, 東洋の田舍者が飛び込んで行くのだから,
怖かつた. (中略) 1900年に私はゲッチンゲン大學へ參りました. (中略) 獨逸は勿論, 世界各國の大學からの, 言はば選り拔きの少壮學士の集合で實際, 數學世界の中心であつた. そこで私ははじめて, 二十五にも成つて, 數學の現狀に後るること正に五十年, といふやうなことを痛感致しました. |
|||
| 文部省がいかなる理由で貞治の「數學研窮」の場を「獨國」と定めたのか, 詳細は不明である. とは言え, 当時の文部大臣外山正一 (1848-1900) は嘗て菊池大麓と共に教授を務めた仲であり, 1897年には菊池が大学を辞して文部次官に就任した事情に鑑みれば, 貞治のドイツ留学は菊池と藤澤の推薦によるものと考えてよいであろう. ドイツでは, 貞治はまずベルリン大学 Universität zu Berlin (現在のベルリン・フンボルト大学) に留学した. 嘗ては, 北里柴三郎 (1853-1931, 微生物学), 高橋順太郎 (1856-1920, 医学), 森鴎外 (1862-1922, 医学) なども留学していた大学である. そこでは, ヴァイエルシュトラス (前出), クロネッカー (前出), クンマー (Ernst Eduard Kummer, 1810-1893) の全盛期が過ぎ, フックス (Lazarus Fuchs, 1833-1902), シュヴァルツ (Hermann Amandus Schwarz, 1843-1921) などが後を継いでいたという. その中でも貞治が影響を受けた数学者は, 若手のフロベニウス (Ferdinand Georg Frobenius, 1849-1917) であった. 彼による整数論やガロア理論の講義は, 講義用のノートも持たずにキビキビとした活きた講義であったという. 但し, 自身の研究 (群の表現論における指標理論など) を学生や留学生たちを相手に講義することはなかったらしい. 洋行直前の貞治は, ドイツから帰朝したばかりの少壮理学者にフロベニウスの怖さを吹聴されたが, 留学時には数学に対する教訓を与えられたと, 次のように述懐している. |
| 「君, フロベニウスの處へ行くなら餘程注意しなければいかぬ」といふのである. それはフロベニウスが學部長かなんかに成つたときに就任演說をやつた,
その時に, ドイツの科學の進歩を大いに自讚したわけである. それで外國人が頻りにドイツへ科學を勉強しに來る. アメリカからも來れば, 何處からも來る.
近頃は日本人すら來る. 今に猿も來るだろう (中略). しかし實際行つて見ると, そんな怖いこともなかつた. 私が何かある問題を持つて, 先生に訊きに行つたことがあつたが, その時先生は, それは面白い, 自分でよく考へなさい, Denken Sie nach! といつていろいろな別刷などを貸してくれた. この「自分で考へなさい」も, 思へば生れて始めての敎訓であつた. |
|||
| 上記のフロベニウスの逸話を伝えた少壮理学者の名前を, 貞治自身は挙げていない. 当時ドイツから帰国したばかりの教授でベルリン留学生と言えば, 長岡半太郎 (1865-1950, 物理学) または大森房吉 (1868-1923, 地震学) であるが, 前者である可能性が高い. [百年史上] (p.183) に掲載されているドイツ留学生で東京帝大の数学関係者は (前出の) 吉江琢兒と中川銓吉 (1876-1942) であるが, 彼らの渡欧出発は貞治よりも後のことである. |
| [森川] 森川潤『明治期のドイツ留学生』雄松堂出版, 2009, 全303頁. | |||
| には, 長岡が明治25年 (1892年) に渡独して, 明治29年 (1896年) に帝大教授に就任したことが記録されている (p.98).
留学先は, フロベニウスの所属するベルリン大学である (p.180). また, 貞治の後年のエッセイ |
| 高木貞治『明治の先生がた』/ 鈴木信太郎編『赤門教授らくがき帖』鱒書房, 1950, pp.111-118. | |||
| には, 貞治が大学で長岡半太郎に教わったこと, 貞治の洋行出発時には長岡が横浜港まで見送りに来てくれたこと, ベルリン留学時代の話をいろいろと長岡から聞いたことなどが記されている.
この著書の中で貞治が「長岡さん」と呼んでいることからも, 貞治と長岡との親しい関係性が窺われる. ベルリンにおける講義の内容は, セレーやヴェーバーの著書を通じて留学前に知り得ていたことが大半であったのであろう. 貞治は「大してこれといふこともなかつた」と述べる一方で,「語學の練習とかに時間を費やさざるを得なかつた」とも述べている. 実際, [本田] によれば, 貞治は当時ドイツで盛んであった演劇を好み,「語学の勉強のためと称して」よく観劇に出かけていたらしい. 王立オペラハウス (Königliche Oper), レッシング劇場 (The Lessing Theatre), ゲーテ劇場 (Goethe-Theater) など, ベルリン市内だけでも20の劇場があったという. |
 F.G.フロベニウス (1849-1917) |
 D.ヒルベルト (1862-1943) |
| その後, 1990年の春に, 貞治はヒルベルト (前出, §2-3)) のいるゲッティゲン大学 (Georg-August-Universität Göttingen) へと移った. この大学には, 貞治より10ほど後に本多光太郎 (1870-1954, 工学) が, 20年ほど後に仁科芳雄 (1890-1951, 物理学) が留学することになる. |
| 一年半の間ゲッチンゲンの雰圍氣の中に棲息してゐる裡に何時とはなく五十年の乘り遲れが解消したやうな氣分になりました. 雰圍氣といふものは大切なものであります. | |||
| ゲッティンゲン大学は, 当時「數學世界の中心」であったが, 貞治はそこでも数学的には関して得るものは少なかったらしい. 無論, 何も得なかったわけではあるまい. 多くの数学書を繙き, 教授達や周囲の学生達と数学に関連した議論を交わす機会も多かったに違いない. とはいえ, 貞治にとってのドイツ留学は, 留学前までに自国で培ってきた数学的素養に対して自信を取り戻したのみならず, 今後は時代を先取りして数学界を牽引しようとする新たな気概まで生じさせる結果となったように思われるのである. 『回顧と展望』の中で, 貞治はヒルベルトとの遣り取りを次のように述べている. |
| 「お前は代數體の整數論をやるといふが, 本當にやる積りか?」とえらく懐疑の眼を以て見られた. (中略) 私のやらうといふのは, 例の「クロネッカーの靑春の夢」と謂はれるものの中で,「基礎のフィールドがガウスの數體である場合, つまりレムニスケート函數の虚數乘法をやらう」と思ふと言つたら,「それはいいだらう」といはれ, … (後略) |
|||
| 『回顧と展望』[速記版] には,「フロベニウスは日本人とアツフエを同じに考へてゐる. その原因はフロベニウスの息子が日本人の友達と附合ふので, フロベニウスの伜の所に來るあの男のやうなものであると思つてゐる」とある (「アツフエ」は "Affe" 即ち「猿」を意味する). フロベニウスの先入観はやや大袈裟であるにしても, ガウス以来, クンマー, ディリクレ, デデキントなどへ継承され, 代数的整数論を華やかに展開してきた当時のドイツ数学界には, 東洋の彼方からやって来る日本人たちを見下すような雰囲気が少なからずあったものと思われる. ヒルベルトから見れば, 極東から来た留学生の数学的学力がどの程度のものなのか怪しかったのであろう. この遣り取りが行われた時期と前後して (1900年8月), ヒルベルトはパリ講演 (第2回国際数学者会議) で, この問題の拡張について (「ヒルベルトの23の問題」の中の「第12問題」として) 言及している. 先述した ([Weber2] p.648 に現れた命題) クロネッカー・ヴェーバーの定理は, \(\mathbb{Q}\,\)を基礎体とする類体の構成問題である. ヒルベルトは, 基礎体を任意の代数体とする類体の構成問題の可能性について述べたのであった. 貞治が「やらう」としたのは, 基礎体\(\,K\!\:\)を虚二次体とする場合である. |
|
楕円関数\(\,f(u)\,\)が虚数乗法をもつ (即ち\(\,\tau\!=\!\omega_{{}_{\!\!\:\!\:2}}\!\:/\omega_{{}_{\!\!\:\!\:1}}\!\in\!K\:\)(但し\(\,\omega_{{}_{\!\!\:\!\:1}}\!\:,\,\omega_{{}_{\!\!\:\!\:2}}\,\)は\(\,f(u)\,\)の周期,
且つ\(\,\mathrm{Im}\!\:\tau\!>\!0\)) ならば任意の\(\,\mu\!\in\!K\,\)について\(\,f(\mu
u)\,\)と\(\,f(u)\,\)に代数的関係がある) とき, 楕円モデュラー関数ないし\(\,j\,\)不変量\(\,j\!\:(\tau)\,\)は\(\,K\,\)におけるアーベル方程式の根であり,
\(\,f(u)\,\)の周期等分点\(\,u\!=\!(\mathbb{Z}\!\:\omega_{{}_{\!\!\:\!\:1}}\!+\!\!\:\mathbb{Z} \!\:\omega_{{}_{\!\!\:\!\:2}}\!\:)/n\,\)に対するヤコビの関数\(\,\mathrm{sn}\,u\,\)は\(\,K\!\:(\!\:j\!\:(\tau))\,\)におけるアーベル方程式の根である. |
|
逆に, 虚二次体\(\,K\!\:\)上の任意のアーベル体が, \(\,j\,\)不変量, 周期等分値により得られ, (前述した) クロネッカーの構成法
(\(\mathbb{Q}\,\)の最大アーベル拡大\(\,\mathbb{Q}^{\mathrm{\!\:ab}}\,\)が\(\,\mathbb{Q}\,\)に\(\,\zeta_{{\!\:}_{n}}\!=\!e^{2\pi
i/n}\,\)を全て添加することにより得られる) と同様の構成法を\(\,K\!\:\)上に見出すこと――これが「クロネッカーの青春の夢」であった. |
| 「青春の夢」(liebster Jugendtraum) なる名称は, ヘンゼル (Kurt Hensel, 1861-1941) の編纂による『クロネッカー全集 第5巻』即ち |
| [Kronecker2] "Leopold Kronecker's Werke" Fünfter Band" B.G. Teubner, 1931. 全527頁. | |||
| において, 第27章におけるデデキント宛の書簡 (1880年3月15日付) の冒頭部 (p.455) に現れる. |
| … dass ich heute die letzte von vielen Schwierigkeiten besiegt zu haben
glaube, die dem Abschlüsse einer Untersuchung, mit der ich mich in den
letzten Monaten wieder eingehender beschäftigt habe, noch entgegenstanden. Es handelt sich um meinen liebsten Jugendtraum, nämlich um den Nachweis, dass die Abel’schen Gleichungen mit Quadratwurzeln rationaler Zahlen durch die Transformations - Gleichungen elliptischer Functionen mit singulären Moduln grade so erschöpft werden, wie die ganzzahligen Abel'schen Gleichungen durch die Kreistheilungsgleichungen. |
|||
| 「この数ヶ月間に亘る困難な研究を克服したと確信している. \(\mathbb{Z}\,\)上のアーベル方程式の根が悉く円分方程式により得られるのと同様, 虚二次体\(\,k\,\)上のアーベル方程式は\(\,k\,\)を虚数乗法にもつ楕円関数の特異モデュライと周期等分点により悉く得られることを証明すること――それは私のお気に入りの若き日の夢だ.」 | |||
| 貞治は, [Hilbert 報文] を通じて, この命題を既に知っていたのであろう. ゲッティンゲンで過ごす間に, 自己の数学的能力に対する自信と矜持を取り戻し, この未解決の問題に取り組む意気込みが芽生えたものと思われる. ところが, ヒルベルトは, 貞治の研究方針について「それはいいだらう」と言ったのみで, 特に何か有益な情報を与えてくれたわけではなかったらしい. フロベニウスから得た教訓「自分で考へ」ることを通じて, 貞治は独りでこの問題に取り組んだのである. |
| 『回顧と展望』において, 貞治は次のように述べる. |
| ヒルベルト自身は, 私が行きました頃は, 整數論から離れてしまつた後で, (中略) ヒルベルトの側にゐたけれども, 直接には何等の指導も受けなかつた. (中略) しかし, 例のレムニスケートの一件だけは, 幼ないものだけれども, 論文を書いてヒルベルトに見せておきました. ヒルベルトはそれをドクトル論文と思つてゐたやうだが, 當時日本にも相當矜持が出來て, 留學生が獨逸のドクトルを取つて來る必要はないといつた時勢になつてゐたから, 私もその論文を持つて歸つて, これを以て學位を頂戴したわけだが, 獨逸土產といへば, まあそれ位のものであつた. |
|||
| ここにおける「レムニスケートの一件」あるいは「獨逸土產」とされる貞治の学位論文『ガウス数体上のアーベル数体について』 |
| [高木6] T.Takagi "Ueber die im Bereiche der rationalen complexen Zahlen Abel'schen Zahlkörper" J. Coll. Sci. Imp. Univ. Tokyo, Vol.19, Art.8, 1903, pp.1-42. | |||
| は, 帰国後に『東京帝國大學紀要 理硏 XIX』に掲載された. 序文および全15節から成る, 貞治が初めて著した (独語による) 本格的な論文である. |
 東京帝国大学紀要 理研 XIX (1903) |
 貞治の学位論文 (1903) の冒頭部 |
| 序文を見ると, まず,「肯定的な解決が待たれる」クロネッカーの命題「虚二次体の相対アーベル数体は, 特異モデュラスをもつ楕円関数の変換方程式から生ずる体で尽くされる」が紹介される. その直後に次のような記載が現れる. |
| … es gibt specielle Fälle dieser grossen Aufgabe, wo man von vorn herein eines ojücklichen Abschlusses sicher sein kann, nämlich die, wo die zu Grunde gelegten quadratischen Körper einclassig: sind, also z.B. durch die dritten und die vierten imajrinären Einheitswurzeln erzeugt werden … | |||
| この偉大なる表明には, 固より解決が保証される特別なケースが存在する, 即ち\(\,\mathbb{Q}\,\)に\(\,\zeta_{{}_{3}}\!=\!e^{2\pi i/3}\,\)または\(\,\zeta_{{}_{4}}\!=\!e^{2\pi i/4}\,\)を添加することで生成される (虚二次体の) 場合である. | |||
| と記されるのである. 但し, この論文で用いられる手法は, (当然ながら) 類体論ではなく, \(\mathbb{Q}\,(\sqrt{-1\!\:}\!\:)\,\)上の不分岐拡大の非存在性およびヒルベルトの分岐理論を用いるものになっている. この論文の主要部は, §9以降であり, |
| Wir kommen nun an den Zielpunkt dieser Abhandlung; es handelt sich darum, nachzuweisen, dass jeder im Bereich, der rationalen complexen Zahlen Abel'sche Körper ein LemnisJcatenhörper ist. | |||
| 論文の目的は, \(\mathbb{Q}\,\)上のアーベル体は悉くレムニスケート体なること | |||
| なる記述で始まる. 「レムニスケート体なること」とは,「ヤコビの楕円関数の等分点を\(\,\mathbb{Q}\,(\sqrt{-1\!\:}\!\:)\,\)に添加して得られる」ことを意味する. 後年, その直後に現れる補助定理に (修正可能ではあるが) 誤りがあることが |
| [近藤] 近藤武『Gauss 数体の Abel 拡大について』/『数学』第15巻第2号 (1963年10月), 岩波書店, p.110. | |||
| において指摘された. 貞治自身, この論文を「幼いもの」と謙遜しているが,「クロネッカーの青春の夢」の一部即ち虚二次体を とする場合に関してこれを肯定的に解決したことは, 当時の学位論文としては驚異的なレヴェルのものであった. 論文の最後に「1901年春, ゲッティンゲンにて」とあることから, ヒルベルトに「レムニスケート函数の虚数乗法をやらうと思ふ」と伝えた時点で, これが肯定的に解決し得る命題であることを貞治は既に看破していたのではないかと思われる. この時点で貞治が一般相対アーベル体の理論まで予想していたかと言えば, それは流石に穿ち過ぎというものであろう. なお, 貞治の言う「これを以て學位を頂戴した」について, 当時の『官報』第6148號 (1903年12月28日付) には次のように記されている. |
| 學位記 岐阜縣平民 從六位 高木貞治 右論文ヲ提出シテ學位を請求シ東京帝國大學敎授會ニ於テ其大學院ニ入リ定規ノ試驗ヲ經タル者ト同等以上ノ學力アリト認メタリ仍チ明治三十一年勅令第三百四十四號學位令第ニ條ニ依リ茲ニ理學博士ノ學位を授ク |
|||
| 論文審査ノ要旨 有理複素數ノ區域内ニ於ケルアーベル「キョルペル」ニ就テ | |||
| 此論文ハ東京帝國大學理科紀要第十九册第五編に掲載セラレタルモノニシテ緒論ノ外ニ第一章ヨリ第十四章ニ至ル十五章ヨリナルモノナリ | |||
| 以下, 40行以上に亘って論文の内容が詳細に説明されている.「官報」であるから一般人も目を通したはずであるが, ここに開陳されているものは専門用語を駆使した本格的な解説であって, 一般読者に対する配慮は一切見られない. 但し,「キョルペル」や「クラッセンツァール」など, (Körper や Klassenzahl のような原語表記がない状態での) カタカナ表記が目立ち, 内容を知る者であっても読みづらいものである. 読み方も言語統一がされておらず,「ウァヰヤルストラスノ「ピー」函数」なる表記も見られる. 況してや専門外の者達には全く意味不明の解説であったことであろう. しかし, 説明内容に誤魔化しは一切なく, 正鵠を射た解説になっている. この解説は次のような表現をもって結ばれる. |
| ……本論文ノ最終ノ目的タル有理複素數ヲ有理區域トナストキハ此區域内ニ於ケルアーベル「キョルペル」ハ「レムニスカーテン, キョルペル」ニ網羅セラルト云フ定理ヲ完全に證明セリ 著者ハ尚ホ本論文ノ目的タル定理ヲ證明セルノ傍硏究ノ餘波或ハ旣知ノ證明ヲ一層簡單ニシ或ハ旣知ノ定理ヲ擴張セリ 以上論文審査ノ結果トシテ本論文ノ提出者タル理學士高木貞治ハ理學博士ノ學位ヲ授與セラルヘキ資格ヲ有スルモノト認定ス |
|||
| 解説文の執筆者名の記載はないが, 内容の専門性から判断して (貞治自身ではないとすれば) 藤澤利喜太郎であろう. 彼のほかに, 貞治の学位論文を理解し得る者 (評価し得る者) は存在しなかったからである. 因みに, 貞治の学位記の前後には, 同時期に学位を授与された者として, 丹羽藤吉郎 (1856-1930, 薬学), 柴田承桂 (1850-1910, 薬学), 松村松年 (1872-1960, 昆虫学), 塚本靖 (1869-1937, 工学) の名が見られるが, 論文内容の詳細な解説が付されているのは貞治と松村のみである. |
| 前節において, [Weber2] 後半部, §179 (p.648) に現れたクロネッカーの命題「\(\mathbb{Q}\,\)上の任意の有限アーベル拡大は円分体である」が「後年の貞治を第一級の数学者へと押し上げる契機となった重要な定理であった」と記した. 但し, この時点で貞治がその重要性を認識していたか否かは判らない. しかし, 後に貞治は『代数的整数論』において, |
| これは Kronecker (1875) が言明し, Heinrich Weber (1886) が証明した有名な定理であるが, 其の後 Hilbert (1896) が (中略) 簡単なる証明を与えた. (中略) 現今では, この定理は類体論の最も簡単なる一例に過ぎない (後略) | |||
| と記すことになる (p.110) のである. なお, "Walfram MathWorld" によれば, ヴェーバーによる "証明" は "incomplete" (不完全) であり,
最初に完全な証明を与えたのはヒルベルトであるという. なお,「類体」なる訳語は貞治の発案であったようであるが (§6-1.参照), その原語 "Klassenkörper" なる用語は貞治の発案によるものではない. 『代数的整数論』p.170 の脚注には, |
| 類体という語は, これよりも狭い意味で, Hilbertが用いた. 尤もこの語は既に楕円函数の虚数乗法論で用いられていた (H.Weber, Algebra, III). | |||
| とある. ヒルベルトが "Klassenkörper" なる用語を掲げたのは, 前掲の [Hilbert 報文] においてであった. 貞治が脚注に挙げたヴェーバーの [Weber3] を見ると, その第23節 §164.には, たしかに "Klassenkörper" の解説がある. しかし, これは [Hilbert 報文] が発表された翌年 (1898年) に出版されたものである. 先述したように, [Weber3] は『楕円関数と代数的数』([Weber4]) の改訂増補版であるから, まず, その原版である [Weber4] を見てみよう. すると, §110. p.439 および §117. p.482 において (綴りの異なる) "Classenkörper" なる用語が見つかった (この年代の書物は索引が付されていないため, 文脈から判断してこの用語の存在を探すほかはない. それゆえ, 他の箇所にも存在する可能性がある). そこには, 次のような記載がある (p.439). |
| Wir betrachten jetzt den algebraischen Zahlkörper, welcher die gemeinschaftliche
Norm aller zu einer bestimmten Determinante \(-m\) gehörigen Körper
der Classeninvarianten erster oder zweiter Art ist, unt der, wie wir im
vorigen Paragraphen gesehen haben, aus den rationalen Functionen einer
Classeninvariante und \(\sqrt{-\!\:m\,}\) besteht. Er kann daherm wenn \((k),(k^\prime),(k^{\prime\prime}),\,\cdots\) dir sämmtlichen Classeninvarianten sind, nach §58, durch \(\frak{K}\,\)\((k,k^\prime,k^{\prime\prime},\cdots)\) oder durch \(\frak{K}\)\(\,(k,\sqrt{-\!\:m\,}\!\:)\) bezeichnet werden. Wir wollen ihn den Classenkörper der Determinante \(-\!\:m\,\) nennen und kurz mit \(\frak{K}\) bezeichnen, während der quadratische Körper \(\frak{K}\)\(\,(\sqrt{-\!\:m\,}\!\:)\) mit \(\varOmega\) bezeichnet sei. |
|||
| ここで扱われるのは, 虚二次体\(\,k\,\)における類不変量および\(\,\sqrt{-\!\:m\,}\,\)の有理関数から構成した「類体」である.
楕円関数の虚数乗法論を用いて,そのガロア群が絶対イデアル類群と同型かつ不分岐であり, 単項化定理を満たすことに言及している. 一方, [Hilbert 報文] pp.175-546 における第15章 §58. の最後には, |
| Satz 94. Wenn der relativ-cyklische Körper K von ungeradem Primzahl-Relativgrade\(\:l\:\)die Relativdifferente\(\:1\:\)in Bezug auf\(\:k\:\)besitzt, so giebt es stets in\(\:k\:\)ein Ideal\(\:\large{\mathfrak{i}}\), welches nicht Hauptideal in\(\:k\:\)ist, wohl aber ein Hauptideal in\(\:K\:\)wird. Die \(l\,\)te Potenz dieses Ideals\(\:\large{\mathfrak{i}}\:\)ist dann notwendig auch in\(\:k\:\)ein Hauptideal, und die Klassenanzahl des Körpers\(\:k\:\)ust mithin durch\(\:l\:\)teilbar. | |||
| 定理94. 有限次代数体\(\,k\,\)に対し, 奇素数次数\(\,l\,\)の不分岐巡回拡大\(\,K\!\!\:/k\,\)が存在するならば, \(k\,\)においては単項イデアルではないが\(\!\:K\!\:\)においては単項イデアルとなる\(\,\large{\mathfrak{i}}\,\)(当然ながら\(\,{\large{\mathfrak{i}}}^{\!\:l}\,\)は\(\,k\,\)の単項イデアル) が存在し, \(k\,\)の類数は\(\,l\,\)で割り切れる. | |||
| が掲げられ, その証明に続けて, |
| Wegen der engen Beziehung, die nach Satz 94 der Körper\(\:K\:\)zu gewissen Idealklassen des Körpers\(\:k\:\)aufweist, werde\(\:K\:\)ein Klassenkörper des Körpers\(\:k\:\)genannt. | |||
| この定理における\(\!\:K\!\:\)と\(\,k\,\)の特定のイデアル類群との密接な関係をもって, \(K\,\)を\(\,k\:\)の類体と称する. | |||
| と記される. 換言すれば, ヒルベルトは「\(K\!\!\:/k\,\)が不分岐の場合, 即ち\(\,k\,\)の一次素イデアルが単項イデアルである場合に限り\(\!\:K\!\:\)の一次素イデアルの積に分解されるとき, \(K\!\:\)を\(\,k\,\)上の類体である」としたのである (『代数的整数論』p.180). これが, 貞治の言う「狭い意味での類体」で, いわゆる「ヒルベルト類体」もしくは「絶対類体」に該当する. では次に, [Weber4] の改訂増補版である [Weber3] を見てみよう. その第23節では, 綴りを改めた "Klassenkörper" 論が展開される. 前半部では, ヤコビおよびヴァイエルシュトラスによる楕円関数の虚数乗法が論じられ, 一次素イデアル, ディリクレ級数などが解説される. 前後を含めた引用は長文になるため割愛するが, 節の後半において, 次のような定義が現れる (p.607). |
| Definition des Klassenkörpers. Die Primideale \(\mathfrak{p}_{{}_{1}}\) ersten Grades der Hauptklasse \(\overline{A}_1\), und nur diese, sollen im Körper \(\mathfrak{K}(A)\) wieder in Primideale ersten Grades zerfallen. |
|||
| 類体の定義. 首類 (単位類)\(\,\overline{A}_1\,\)に属する一次素イデアル\(\,\mathfrak{p}_{{}_{1}}\,\)のみが体\(\,\mathfrak{K}(A)\,\)の一次素イデアルに再び分解される. |
|||
| この引用箇所のみでは正確な表現ではないが, 前後の文脈と併せて判断すれば, イデアルの合同類別に着目し, 単項化定理から離れて一次素イデアルの完全分解性をもって類体を把捉するもので,
これは現行の定義に沿うものと言ってよい. ヴェーバーは, ヒルベルトのイデアル類群の概念を拡張し,「次数\(\,n\,\)のガロア拡大\(\,K\!\!\:/k\,\)が類数\(\,h\,\)の合同イデアル群\(\,H\,\)に対応し, \(h\!=\!n\,\)である (すなわち\(\,H\!\:\)に属する絶対次数1の素イデアル\(\,\mathfrak{p}\,\)が\(\,k\,\)の単項イデアルで, \(\mathfrak{p}\,\)が全て\(\!\:K\!\:\)の一次素イデアルに分解される) とき, \(\,K\,\)を\(\!\:H\!\:\)に対応する類体と称する」としたのである (『代数的整数論』p.170). |
| 1901年, ドイツ留学から帰国した貞治は, 留学中に助教授の辞令を受けていた. 1903年に (先述した) 学位論文 [高木6] が認められると, 翌1904年, 29歳で東京帝国大学理科大学 (現在の東大理学部) の教授に就任した. 引き続き,『回顧と展望』を見てみよう. |
| 1901年に歸つて來てからは, いろいろな講義をさせられた. 代數曲線とか, その他何をやつたか忘れてしまつたが, (中略) その裡に, 吉江君や,
中川君が歸つて來られて, 私もさういふ餘計な仕事はやらなくて濟むやうになつた. 全體私は殊にさういふ人間であるが, 何か刺戟がないと何もできない性質である. 今と違つて, 日本では, つまり「同業者」が少いので自然刺戟が無い. ぼんやり暮してゐてもいいやうな時代であつた. |
|||
| [百年史上] (p.172) によれば, 1901年~1904年当時, 数学科の講座を受け持っていたのは, ・第一講座 [幾何学] 藤澤利喜太郎 (1898.7-1903.9), 坂井英太郎 (1903.9- ) ・第二講座 [関数論] 藤澤利喜太郎 (1893.9- ) ・第三講座 [代数学] 高木貞治 (1901.12- ) ・第四講座 [微分方程式論] 吉江琢兒 (1902.9- ) ・応用数学講座 長岡半太郎 (1896.9-1901.9) であった (括弧内の年号は担当期間を表す). 初代教授の菊池大麓は, 1898年より総長に就任しており, 講座担当から外れていた. また, 応用数学講座は, 1901年9月以降, 理論物理学講座と改称され物理学科の所属となったという. 上記引用文中の「中川君」は, 前出 (§2-4) の中川銓吉を指す. 中川は, 1898年に東京帝大を卒業し, 第二高等学校 で教鞭を執った後にベルリン留学を経て, 帰国後の1907年5月から第一講座を担当したという ([百年史上] pp.155, 171-172, 183). 帰国後の貞治は, 教授として学生の指導に携わる中で, 数学者としての業務以外の仕事も任されたのであったのであろうか.「餘計な仕事」が何を指すものかは不明であるが, 帰国後の貞治は, 類体論に関する論文を発表する1914年までの10年間, 学位論文ないし類体論に関連した論文を発表しなかった. この時期の事情について, 本田欣哉は「一見スランプとも考えられるわけであるが, これはやはり高木の個人的な性格に関係した現象であろう. (中略) 小さな研究論文ばかりを次々と発表して行くやり方は, あまり好まなかったようである.」と述べている.「この10年間の無風状態の間に, 数学の学力を深め充実して行ったのであって, それがのちに, 代数学と解析学を縦横に用いる, 類体論の深い複雑な研究の土台となっている」という ([科学技術史] pp.211-212). 貞治の論文集 |
| [高木全集] "The Collected Papers of TEIJI TAKAGI" 岩波書店, 1973. 全266頁. | |||
| に収録されている計26編 (英文14編, 独文10編, 仏語2編) の論文中, 最初の6編は1903年以前に発表されたものである. |
 高木貞治論文全集 (岩波書店, 1973) |
 第2版 (シュプリンガー東京, 1990) |
| 以下, [高木全集] に収録されている論文を順に見てみよう. 1903年以前に発表された論文のうち, 5編 (英文) は,『東京數學物理學會報告』に掲載された |
| [高木1] T.Takagi "On Weierstrass' proof of the fundamental theorem of algebra" Proc. Phys.-Math. Soc. Japan, Ser.II, Vol.1, 1902, pp.56-58. | |||
| [高木2] T.Takagi "On the 'zweigliedriger Modul" Proc. Phys.-Math. Soc. Japan, Ser.II , Vol.1, 1902, pp.102-103. | |||
| [高木3] T.Takagi "A simple example of the continuous function without derivative" Proc. Phys.-Math. Soc. Japan, Ser.II, Vol.1, 1903, pp.176-177. | |||
| [高木4] T.Takagi "Mathematical notes" Proc. Phys.-Math. Soc. Japan, Ser.II , Vol.2, 1903, pp.25-29. | |||
| [高木5] T.Takagi "A simple proof of the law of reciprocity for quadratic residues" Proc. Phys.-Math. Soc. Japan, Ser.II, Vol.2, 1903, pp.74-78. | |||
| であり, この論文集において僅か2,3ページ程度の (本田の言う)「小さな研究論文」である. とは言え, 何れも貞治の独自の視点に基くオリジナル性に富んだ研究であり, 味わい深い内容をもっている. 例えば, [高木1] 『ヴァイエルシュトラスによる代数学の基本定理の証明』では, 単なるヴェイルシュトラスの手法の紹介に留まらず, より洗練された形へと改良が施された証明が紹介されており, [高木3] 『導関数が存在しない連続関数の簡単な例』においても貞治独自の優れたセンスが際だつもので, 後に「高木曲線」として知られるフラクタルの実例がここに見出される (この曲線は, 後年の『解析概論』でも解説される). また, [高木5] 『平方剰余の相互法則の簡単な証明』では, ガウスによる第三証明が幾何学的手法をもって簡明な形に改良された証明が開陳されているのである. これらより前に書かれた論文が, 貞治の学位論文, 即ち前出 (§2-5) の [高木6] であった. これらの論文を著した後, 10年もの間, 貞治は論文を全く発表しなかった. とは言え, 貞治が「ぼんやり暮してゐて (中略) 何もしないでゐた」はずはない. 学位論文を発表した時点で, 数学研究における貞治の目標は既に確定していたことであろう.「クロネッカーの青春の夢」の解決, さらにはヒルベルトのパリ講演における「類体の構成問題」の解決である. 1914年から1917年にかけて, 学位論文に続く5編の論文 (英文1編, 独文4編) が『東京數學物理學會記事』に立て続けに発表されることになる. |
| [高木7] T.Takagi "On a fundamental property of the "equation of division" in the theory of complex multiplication" Proc. Phys.-Math. Soc. Japan, Ser.II, Vol.7, 1914, pp.414-417. | |||
| [高木8] T.Takagi "Zur Theorie der relativ-Abel'schen Zahlkörper I" Proc. Phys.-Math. Soc. Japan, Ser.II, Vol.8, 1915, pp.154-162. | |||
| [高木9] T.Takagi "Zur Theorie der relativ-Abel'schen Zahlkörper II" Proc. Phys.-Math. Soc. Japan, Ser.II, Vol.8, 1915, pp.243-254. | |||
| [高木10] T.Takagi "Zur Theorie der komplexen Multiplikation der elliptischen Funktionen" Proc. Phys.-Math. Soc. Japan, Ser.II, Vol.8, 1915, pp.386-393. | |||
| [高木11] T.Takagi "Über eine Eigenschaft des Potenzcharacters" Proc. Phys.-Math. Soc. Japan, Ser.II, Vol.9, 1917, pp.166-169. | |||
| さらに, 1919年には,『日本數學物理學會記事』に『ノルム剰余について』 |
| [高木12] "On norm-residues" Proc. Phys.-Math. Soc. Japan, Ser III, Vol.2, 1919, pp.43-45. | |||
| が発表された. これらの標題 ([高木7]『虚数乗法論における等分方程式の或る基本性質』, [高木10]『楕円関数の虚数乗法論について』, [高木11]『冪剰余記号の或る特性について』など) から察し得るように, これら一連の論文は各々が類体論の一部を成すものである. 貞治は, ヴェーバーによるイデアル類群の拡張を採り入れ, ヒルベルトの絶対類体における不分岐性を取り除く方針で類体論創設の土台を構築していったのであった. この方針のもとで, [高木8] 『相対アーベル数体論について 第一』において類体の存在を示すに至ったのである. 但し, この論文では簡潔に論拠が示されたのみであった. |
| 完全な証明が施されたのは, その翌年に『東京帝國大學理學部紀要 XLI』に発表された『相対アーベル体の理論』 |
| [高木13] T.Takagi "Ueber eine Theorie des relativ Abel'schen Zahlkörpers" J. Coll. Sci. Imp. Univ. Tokyo, Vol.41, Art.9, 1920, pp.1-133. | |||
| においてである (1920年7月31日出版). この研究過程に関して,『回顧と展望』では次のように回想されている. |
| 1914年に世界戰爭が始まつた. それが私にはよい刺戟であつた. 刺戟といふか, (中略) ネガティヴの刺戟だが, つまりヨーロッパから本が來なくなつた.
(中略) 學問をしようといふなら, 自分で何かやるより仕方が無いのだ. (中略) 「類體論」の話を少しすると, あれはヒルベルトに騙されてゐたのです. 騙されたといふのは惡いけれども, つまりこつちが勝手に騙されてゐたのです. ミスリードされたのです. (中略) ヒルベルトは, 類體は, 不分岐だといふのであるが, (中略) そんな風に私は思はされた. 所が, 本が來なくなつて, 自分でやり出した時に, さういふ不分岐などといふ條件を捨ててしまつて, 少しやつてみると, (中略) 要するにアーベル體は類體なりといふことにぶつかつた. 當時これは, あまりにも意外なことなので, それは當然間違つてゐると思うた. (中略) 何が間違ひか, 實例を探して見ても, 間違ひの實例が無い. |
|||
| ヒルベルトによる絶対類体\(\,K\!\!\:/k\,\)は, 代数関数論との関連性から現れ, リーマン面の分岐理論に基く不分岐拡大に着想を得たものであった. 貞治は, [高木13] の序文において, [Hilbert 報文] および |
| [Hilbert1] D.Hilbert "Über die Theorie der relativ Abel'schen Zahlkörper" Nachr. Gesell. Wiss. Göttingen, 1898. | |||
| [Hilbert2] D.Hilbert "Über die Theorie der relativ quadratishen Zahlkörper" Math. Ann. Vol.51, 1899. | |||
| [Furtwängler1] P.Furtwängler "Allgemeiner Existenzbeweis für den Classenkörper eines beliebigen algebraischen Zahlkõrpers" Math. Ann. 63, 1907. | |||
| [Fueter] R.Fueter "Abel'sche Gleichungen in quadratisch-imaginären Zahlkörpern" Math Ann. Vol.75, 1914. | |||
| と共に, 重要かつ影響を受けた参考文献として挙げている. |
| [Hilbert1] および [Hilbert2] において, ヒルベルトは,「\(K\!\!\:/k\,\)はヒルベルト類体 (最大不分岐アーベル拡大) で, そのガロア群は\(\,k\,\)の狭義イデアル類群と同型であること,
\(k\,\)の素イデアル\(\,\mathfrak{p}\,\)の\(\,K\!\!\:/k\,\)における分解の様相は\(\,\mathfrak{p}\,\)の属する狭義イデアル類により定まり,
\(\mathfrak{p}\,\)が総正な単項イデアルである場合のみ\(\,\mathfrak{p}\,\)は\(\,K\!\!\:/k\,\)で完全分解すること,
\(k\,\)のイデアルは全て\(\,K\,\)の単項イデアルとなること」を類体の諸性質として記していたのであった. |
| フルトヴェングラーは, [Furtwängler1] において, 一般の有限次代数体に対するヒルベルト類体の存在を示した. ただし, ヒルベルトの言う「類体の諸性質」(上記において, \(K\,\)が最大不分岐アーベル拡大体なることや,
最後に掲げた「単項化定理」など) は, この時点では解決できていなかった. |
| 一方, フェターは [Fueter] において, 虚二次体\(\,K\,\)の奇数次アーベル拡大体は\(\,K\,\)に特異モデュラス \(j\!\:(\tau_{\!\!\:{}_{\!\:K}}\!\:)\,\)と\(\,\zeta_{\!\:n}\!=\!e^{2\pi i/n}\,\)を添加した拡大体に含まれることを示していた. これは「クロネッカーの青春の夢」に繋がるものであり, 貞治の研究意欲に刺戟を与えたであろうと思われる. |
| 貞治は, 最初はヒルベルトと同様に不分岐性を前提条件として考究を進めたが,「クロネッカーの青春の夢」を念頭に置く中で, ヴェーバーのように分岐性を視野に入れて考えるようになった. [高木13] では, 分岐をもつアーベル体を追究していった結果,「アアベル体即ち類体という帰結」(『代数的整数論』序) を得たのである. 貞治は, そのような事情をもってヒルベルトに「ミスリードされた」と述べたのである. [高木13] は, [高木全集] 全266頁のうち約3分の1 (72~167頁) を占める長大な論文であり, 序文と5つの章から構成される (以下に用いられる記号は, 論文におけるそれとは異なるものを採用している). |
| 第1章「一般類体論」"Der allgemeine Classenkörper" では, 合同類群や導手に関して言及され, Satz6に基いて類体の一意性が示される. ここでは, \(l\,\)を奇素数として\(\,l\,\)次巡回拡大\(\,K/k\,\)の分岐イデアルに必要な導手\(\,\mathfrak{f}\,\)が設定され, \(K\,\)に対応する合同イデアル群\(\,\mathfrak{H}\,\)が\(\,K/k\,\)のイデアルのノルムにより規定されている. |
| 第2章「素数次相対巡回体の種の理論」"Die Geschlechter im relativ cyclischen Körper
vom Primzahlgrade" では, ノルム剰余やアンビグ (特異) 類および類の種 (Geschlecht) に言及され,
類体の基本定理が (証明は後述するとして) 提示される (Satz 13). |
| 第3章「一般類体の存在証明」"Existenzbeweis für den allgemeinen Classenkörper"
では, 奇素数次の場合, 素数冪次の場合, 一般の場合に分けて, 類体の存在定理が証明される (Satz 23). |
| 第4章「他の諸定理」"Weitere allgemeine Sätze" では,「相対アーベル体は類体」なることが提示され
(Satz 28), それまでの諸結果と併せて同型定理 (Satz 29) および分解定理 (Satz 30) が示される. |
| 第5章「楕円関数の虚数乗法論への応用」"Anwendung auf die Theorie der complexen Multiplication der elliptischen Functionen" では, 類体論の諸結果が「クロネッカーの青春の夢」に適用され (Satz 37), 論文は締め括られるのである. |
| 以下, |
| [彌永数論] 彌永昌吉『数論』岩波書店, 1969, pp.448-487. | |||
| [河田数論] 河田敬義『数論』岩波書店, 1992, pp.393-429. | |||
| [谷山全集]『[増補版] 谷山豊全集』日本評論社, pp.183-198, pp.212-220, pp.337-345. | |||
| [百年史下]『日本の数学100年史 下』岩波書店, 1984, pp.64-73, pp.241-248. | |||
| などを援用して, 貞治がこれら論文を発表した頃とその後の状況について概観しよう. |
 彌永昌吉『数論』(岩波書店, 1969) |
 河田敬義『数論』(岩波書店, 1992) |
| 代数体\(\,k\,\)の拡大体を\(\,K\,\)とし, 整イデアル\(\,\mathfrak{m}\,\)(有限素点および無限素点の形式的有限冪積) と互いに素なる\(\,k\,\)の分数イデアルの成す乗法群\(\,\mathfrak{A}_{\mathfrak{m}}\,\)と, 射類\(\,\mathfrak{S}_{\mathfrak{m}}\,\)(\(=\!\{(\alpha)\,;\,\alpha\!\equiv\!1\, \mathrm{mod}.\!\!\:\mathfrak{m}\}\,\)(\(\alpha\,\)は総正)) により得られる射類群\(\,\mathfrak{A}_{\mathfrak{m}}/\mathfrak{S}_{\mathfrak{m}}\,\)の部分群\(\,\mathfrak{H}_{\mathfrak{m}}/\mathfrak{S}_{\mathfrak{m}}\,\)を考える. \(K\!\!\:/k\,\)がガロア拡大であり, \(\mathfrak{m}\,\)と素なる一次素イデアル\(\,\mathfrak{p}\,\)が\(\,\mathfrak{p}\!\in\!\mathfrak{H}_{\mathfrak{m}}\,\)なる場合に限り\(\,K\,\)の一次素イデアルの積に完全分解されるとき, \(\,K\,\)を\(\,\mathfrak{H}_{\mathfrak{m}}\,\)の類体として定義する. ヒルベルトが定義した意味での類体は, \(\mathfrak{m}\!=\!(1)\,\)(\(\mathfrak{H}_{\mathfrak{m}}\,\)が単項イデアル群) となる場合に過ぎない. 貞治は, この (ヒルベルト類体よりも拡張された) 類体に関して, 次の諸定理を示したのである. |
| i)\(\!\:\!\:\:\:\:\)類体の一意性 \(k\,\)におけるイデアル群\(\,\mathfrak{H}_{\mathfrak{m}}\,\)上の類体\(\,K\,\)は (存在するならば)
一意的である. ii)\(\,\:\:\)存在定理 \(k\,\)における任意のイデアル群\(\,\mathfrak{H}_{\mathfrak{m}}\,\)に対応する類体\(\,K\,\)が存在する. iii)\(\,\:\)分岐定理 類体\(\,K\!\!\:/k\,\)の導手は\(\,K\!\!\:/k\,\)において分岐する\(\,k\,\)の全ての素イデアルを含む. iv)\(\,\,\)同型定理 類体\(\,K\!\!\:/k\,\)のガロア群は\(\,k\,\)における類群\(\,\mathfrak{A}_{\mathfrak{m}}/\mathfrak{H}_{\mathfrak{m}}\,\)と同型である. v)\(\:\:\!\:\)分解定理 素イデアル\(\,\mathfrak{p}\!\in\!\mathfrak{H}_{\mathfrak{m}}\,\)は, \(\mathfrak{p}^f\!\in\!\mathfrak{H}_{\mathfrak{m}}\,\)となる最小の\(\,f\,\)に対して, 類体\(\,K\!\!\:/k\,\)において\(\,f\,\)次の素イデアルに分解される. |
|||
| 中でも最も重要な定理は, 彌永が「高木理論の驚嘆すべき結果」([彌永数論] p.466) と称する |
| Satz 28. Alle relativ Abel'schen Körper in Bezng auf einen beliebigen algebraischehen Körper werden durch die Classenkörper nach den Idealmoduln in demselben erschöpft. | |||
| vi) 基本定理 代数体\(\,k\,\)の全てのアーベル拡大は\(\,K\,\)は, \(k\,\)の或るイデアル群\(\,\mathfrak{H}_{\mathfrak{m}}\,\)に対する類体である. | |||
| であった. これは, 当時の貞治自身でさえ「当然間違つてゐると思」ったほど「あまりにも意外なこと」であったのである. 余談であるが, [高木13] の序文に重要かつ影響を受けた参考文献として挙げられた [Furtwängler1] や [Fueter] に関して, 貞治は『回顧と展望』[速記版] に後日談を打ち明けている. |
| いろいろ人のやつたものを讀んでフルトヴェングラー, フユーターを讀んだといふけれども, 實はさう詳しくは讀まなかつた. フユーターで想ひ出しましたが, その頃フユーターが出したものを諸君御存知ないかも知れませぬけれども, 數學のあゝいふ雜誌に無粹だらうと思ふのです. クロネツカーの問題が解けたといふ意味で, 大きな何號活字といふのですか, 表題に使ふやうな活字でそのことを印刷したものです. クロネツカーのあれが實現されたといふやうなことを今でも記憶してゐるのですけれども, 御覽になつた方があるかも知れませぬが, 讀んで見るとやはりよく判らないし面白くなかつた. |
|||
| ここにも数学に対する貞治の真摯な姿勢が垣間見える. 数学者は数学的な真理を見極めることに主眼をおくべきであり, その研究成果を (スポーツ競技で勝利したかのように) 大袈裟に飾り立て騒ぎ立てて宣伝するようなことは数学者としてあるいは数学誌においては相応しくない, と述べたのである. また,「よく判らないし面白くなかつた」なる表現も, 分からないものについては分かったフリをしないという, 貞治の姿勢が窺える. 数学的な内容として面白いか面白くないかについても, 後年, 貞治が学生達を指導する際の一つの基準として用いたようである (これに関しては最終節 (§6) で触れることにする). |
| [高木13] を完成した貞治は, 直ちに, 仏語による報告書『代数的整数論における幾つかの一般的な定理について』 |
| [高木14] T.Takagi "Sur quelques théorèmes généraux de la théorie des nombres algébriques" C.R. Congrès Internat. Math. Strassbourg, 1920, pp.185-188. | |||
| を書き上げた. これは, 1920年にストラスブールで開催された万国数学者会議に間に合わせるために書かれた研究報告である. 貞治はここで, 自身の「類体論」に関する結果を初めて国際的な学会で発表したのであった. この会議の模様について, |
| [本田5] 本田欣哉『高木貞治の生涯』/ 日本評論社『数学セミナー』1975年5月号, pp.40-41. | |||
| には (小倉金之助の談話をもとに) 次のように書かれている. |
| 高木は日本代表として挨拶をのべたが, その中で, 敗戦国ドイツの数学者がこの会議からしめ出されていることに, 遺憾の意を表明した. (中略) コングレスでは, 毎日9時から12時まで, 講演が行なわれ (中略) ひとり20分の割り当てであった. 高木は, 第4日の (中略) 10時ごろから, その講演を行なった. 標題は「代数体の理論のいくつかの一般的定理について」で (中略) 黒板には何も書かず, フランス語の原稿をただよみつづけた. |
|||
| 貞治自身は, 帰国後の講演記録 |
| 高木貞治『すとらすぶるぐニ於ケル數學者大會ノ話』/『日本中等敎育數學會雜誌』第3巻第4-5号, 1921, pp.113-116. | |||
| において, |
| 今度ノ數學者大會ハ昨年9月22日カラ9月30日マデノ間佛國ノ新領土あるさすノすとらすぶるぐデ開カレタノデス. (中略) 講演ハ四部に分レ 第一部 整數論代數學及ビ函數論 第ニ部 幾何學 第三部 應用數學 第四部 數學歴史, 敎授法等 少ナイ部ハ十二三名カラ多イノハ三十四五位名アリマシタ. (中略) 四部を同時ニ聽クコトハ出來ヌノデ銘々勝手ニ好キナノヲ聞クコトニナリマス (後略) |
|||
| と述べ (pp.113-114), 独墺など反連合国側 (中央同名国側) の国々が学会から排除されていたことへの批判にかなりの紙面を割いた後, 肝心の (多くの読者が詳しく知りたいと思っていたであろうところの) 貞治自身の発表については, 末尾に |
| 本邦人ノ參會者ハ大阪ノ小倉博士ト小生トノ二人デ小倉君ハいんたーぽれーしよんノ理論ニツキテ講演セラレ, 小生ハ整數論ニ關スル硏究ノ結果ヲ披露致シマシタ. | |||
| なる一文のみを記して (p.116) 学会報告を終えてしまっている. 上掲の [高木14] の内容は先述した諸定理の結果を纏めたものであり, そのまま話せば恐らく15分程度の時間は直ちに経過してしまったことであろう. 貞治自身の『回顧と展望』によれば, |
| 戰爭の直後, 聯合國とドイツ側と分離した時代で, (中略) 整數論の話などを持出すには最も不適當な所であつた. 類體論などに理解を持つた人は僕の知つてゐる所では二三人位で, 先づフューター, あれはスウィス人だから來てゐた. それから佛蘭西ではシャトレといふ人, その外ではアダマール, 彼は問題を理解する. 興味を有つか, 有たんかは知らんが, 問題を理解する人である. まあ當てになるのは, こんな連中だけであつた. なんでもあの時, レセプションの晩に, 私の近くで,「あの日本人が整數論の話をするといふではないか. 多分フェルマーをやるんだらう. こいつは面白いぞ」などと私語するのが聞えて, 私は苦笑した. 會議では15分位の講演をしたけれども, 無論, 反響も何もありはしない. |
|||
| という状況であった. 嘗てのドイツと同様, ここでも日本人による数学研究が西欧では如何に軽んじられていたかが窺える. 彼らから見れば, 身のほど知らずの日本人が国際会議に押しかけて来て, 数学愛好家にありがちな「フェルマーの最終定理」の一部をかじって愚にもつかない成果を発表しようとしているとでも思ったのであろう. 小倉金之助も,「その会議に出席した日本人は, 高木先生と私の二人でした」と述べ, 貞治の講演に関しては「何しろごく短い時間で, (中略) 先生の講演には誰の質問も議論もありませんでした.」と記している (前掲書 [小倉] p.351). 類体論に最も深い興味関心を示したはずのドイツ人数学者達にこの講演を聞かせることが適わなかったことは, 貞治にとって大きな不運であった. 理解される可能性が低いどころか無名の東洋人を嘲笑するような雰囲気の中で「無論, 反響も何もありはしない」ことを予想し,「黒板には何も書かず, フランス語の原稿をただよみつづけた」貞治の無念さは, 察するに余りある. このとき既に45歳になっていた貞治であったが, 国際的には全くの無名の存在であったのである. フェター (前出) は, [高木13] の序文に記載されている通り, [Fueter] を著した数学者であるから, 貞治の講演には少なからず関心を抱いたと思われるが, 彼も何の反応も示さなかったとすると, 講演内容を理解できなかったか, あるいはその意外な結論に対して半信半疑であったか, の何れかであろう (後年になってフェターが貞治の理論を高く評価するようになったことは, 現在ではよく知られている). 貞治は, この報告書の最後で, 今後取り組むべき「代数的整数論における重要な問題」として「非アーベルな正規拡大と基礎体のイデアル群とは一意的に対応するか否か」を掲げた. これはさらにレヴェルの高い問題であり, 類体論の重要性を含め, これがその後の数学者達によって重要な研究対象であることを認識されるまでには, しばらく時間を要することとなる. [本田5] によれば, 貞治はこの講演の後, ドイツに立ち寄ったという.「旧師ヒルベルトやランダウに会ったが, この地の整数論の若手にジーゲルという俊秀がいることをきき及んだ」という. 帰国後, 貞治はジーゲル (Carl Ludwig Siegel, 1896-1981) 宛に [高木13] の別刷を送った. 貞治の立場からすれば当然であるが, ドイツの数学者達に真先に類体論の成果を伝えたかったのであり, 結果的には, ジーゲルに論文を送ったことが類体論を広める重要な契機となったのであった. その後, |
| [高木15] T.Takagi "Sur les corps résolubles algébriquement" C.R. Acad. Sci. Paris, Vol.171, 1920, pp.1202-1205. | |||
| [高木16] T.Takagi "Note on the algebraic equations" Proc. Phys.-Math. Soc. Japan, Ser.III, Vol.3, 1921, pp.175-179. | |||
| の2篇の短い論文が書かれ, [高木15]『代数的に可解な体について』は『科学アカデミー』 ('Académie des Sciences') に, [高木16]『代数方程式に関するノート』は『日本數學物理學會誌』に発表された. 前者は, 三次剰余と原始二次形式の類数に関するデデキントの結果を素数次の拡大体の場合に一般化したもので, 仏国滞在時のものらしく仏文で執筆されている. 後者は, グレース (John Hilton Grace, 1873-1958) の無極性定理に基いて微分合成多項式の零点の位置を特定するもので, 英文で執筆された. [高木13] を類体論に関する第一論文とすれば,『東京帝國大學理學部紀要 XLIV』に発表された『任意の代数体における相互法則について』 |
| [高木17] "Ueber das Reciprocitätsgesetz in einem beliebigen algebraischen Zahlkörper" J. Coll. Sci. Imp. Univ. Tokyo, Vol.44, Art.5, 1922, pp.1-50. | |||
| は, 類体論に関する第二論文となる. ここに掲げられた参考文献は, ヒルベルトのものに関しては [高木13] の場合と同様であるが, フルトヴェングラーのものに関しては, |
| [Furtwängler2] P.Furtwängler "Über die Reziprozitätsgesetze zwischen \(l^{\!\:\mathrm{ten}}\) Potenzresten in algebraischen Zahlkörpern, wenn \(l\) eine ungerade Primzahl bedeutet." Math. Ann. Vol.58, 1904. | |||
| [Furtwängler3] P.Furtwängler "Die Reziprozitätsgesetze für Potenzreste mit Primzahlexponenten in algebraishen Zahlkörpern" Math. Ann. Vol.67, 1909, Vol.72, 1912, Vol.74, 1913. | |||
| となっている. [高木17] は, ヒルベルトのパリ講演 (第2回国際数学者会議) における「任意の代数体における一般相互法則」(「ヒルベルトの23の問題」の中の「第9問題」) に関する論文である. この問題については, 既にフルトヴェングラーが |
| [Furtwängler4] P.Furtwängler "Allgemeiner Existenzbeweis für den Klassenkörper eines beliebigen algebraischen Zahlkörpers" Math. Ann. Vol.63, 1904. | |||
| において奇素数次に関して証明し, 続いて [Furtwängler3] において全ての素数冪次に関して冪剰余の相互法則を示していた. 貞治は, 類体論を応用してフルトヴェングラーの方法よりも洗練された形で任意の素数冪に関する相互法則を示したのである. さらに, \(k\,\)を基礎体とするクンマー拡大\(\,K\!\!=\!\!\:k\!\:(\sqrt[l\!\:]{\mu\,})\,\)(\(\,l\,\)は奇素数, \(\mu\!\in\!k\,\)) に対応する\(\,k\,\)のイデアル群\(\,\mathfrak{H}(K\!\!\:/k)\,\)の導手を\(\,\mathfrak{f}\,\)とするとき, \(k\,\)のイデアル\(\,\mathfrak{a}\,\)に対応する\(\,l\:\)冪剰余記号\(\,\displaystyle{\left(\!\frac{\!\:\mu\!\:}{\mathfrak{a}}\!\right)}\,\)の値は, \(\mathrm{mod}.\mathfrak{f}\,\)で\(\,\mathfrak{a}\,\)が属する剰余類のみで定まることを明示し, 後にアルティン (Emil Artin, 1898-1962) により証明される「一般冪剰余の相互法則」を予見したのであった. [高木17] の末尾を見ると,「1920年6月に完成」とある. 類体論に関して述べた2篇の主論文 (第一, 第二) は, 発表年月には2年ほどの差異はあるものの, それまでの研究の成果を纏めて一気に書かれたものらしい. |
| 発表当時は冷遇された「高木類体論」がその後, 如何にして世界に知られ, 高く評価されるようになったか. その経緯について, [本田5] に詳細なる記載がある. まず, その契機について引用してみよう. |
| ある日のこと, ジーゲルとアルチンが代数体の話をしていたときに, ジーゲルは, 高木が送った論文をアルチンに示して, よんで見ないかとすすめた.
(中略) 晩年のアルチンに会った筆者に,「非常な讃歎の念をおぼえた. 難解ではなかった. むしろ, 一切が明晰であった」と語っている. アルチンは高木に, 自分にも別刷を1部送ってくれるよう, 依頼の手紙を出した. それはやがて届き, さらに第2論文の別刷も送られてきた. (中略) アルチンが, 相互法則の最も一般的な形を, フロベニウス置換により定式化するアイディアを得たのは, 1923年のことで, それは高木の第2論文から示唆されたのである. |
|||
| 貞治から論文を送られたジーゲルが, 新進気鋭の若手数学者, 24歳のアルティン (前出, §3-4) にその論文を薦めたことが, 後年, 広く類体論が知られるようになったことの発端であったようである. アルティンは, フロベニウスの非可換環に対する群指標の理論をもとにガロア群の指標に対する\(\,L\,\)関数を導入した. 類体論における同型定理と分解定理を, 基礎体の素イデアルとそのフロベニウス置換とを対応させることにより, |
| [Artin] E.Artin "Beweis des allgemeinen Reziprozitätsgesetzes" Abh. Math. Semin. Univ. Hambg. Vol.5, 1927, pp.353–363. | |||
| において,「一般相互法則の証明」を次のような形で示したのであった. |
| \(k\,\)の有限アーベル拡大\(\,K\!\!\:/k\,\)で不分岐な\(\,k\,\)の素イデアル\(\,\mathfrak{p}\,\)(その絶対ノルムを\(\,N\mathfrak{p}\,\)とする) に対し, 任意の整イデアル\(\,\alpha\!\in\!K\,\)が\(\,\sigma\alpha\!\equiv\!\alpha^{N\mathfrak{p}}\:(\mathrm{mod}\,\mathfrak{p})\,\)を満たすような, 有限アーベル拡大\(\,K\!/k\,\)のガロア群\(\,G(K\!\!\:/k)\,\)の元\(\,\sigma\!=\!\displaystyle{\left(\!\frac{\!\:K\!\!\:/k\!\:}{\mathfrak{p}}\!\right)}\,\)(アルティン記号) が定まることをもって, \(K\!\!\:/k\,\)を\(\,k\,\)のイデアル群\(\,\mathfrak{H}(K\!\!\:/k)\,\)に対応する類体とするとき, \(\sigma\,\)は\(\,\mathfrak{p}\,\)が属する\(\,\mathrm{mod}\,\mathfrak{H}\,\)の剰余類のみにより定まり, この対応により\(\,\mathrm{mod}\,\mathfrak{H}\,\)の剰余類と\(\,G(K\!\!\:/k)\,\)が同型となる. ―― |
| 一方, 類体論の価値を認め, 広く知らしめた最初の人物は, アルティンと同年代の若手数学者ハッセ (Helmut Hasse, 1898-1979) であった. |
| 再度 [本田5] から引用する. |
| ハッセが高木の論文のことを知ったのは, 1923年にハンブルクで, アルチンにすすめられてであった. ハッセは高木の第1論文をよむのに, 数週間を要した.「その一般性, その明晰さ, 効果的な方法とおどろくべき諸結果とに, 深く魅惑された」と筆者に語っている. (中略) ハッセは高木の論文を徹底的に分析究明し, 困難な諸定理の証明を, 独自の方法で整理し, 明快にしていった. …… 1925年 (中略) ドイツ数学者協会年会において, ハルレ大学教授ヘルムート・ハッセ (27歳) は,「類体論の最近の発展について」と題する講演を行い, 高木の理論の大要を紹介した. (中略) ついでハッセは, この講演を敷衍した,「代数体の理論の最近の研究と問題に関する報告」と題するくわしい総合報告を, 協会の年報に3回 (1926, 27, 30年) に亙り発表した. ハッセの独自の整理を行なった, 完全な証明つきの報告である. ハッセの講演と報告は, 高木の類体論を世界の数学界に紹介するのに, 決定的な役割を演じた. |
|||
 E.アルティン (1898-1962) |
 H.ハッセ (1898-1979) |
| ここに挙げられている3回の年報報告 ([Hasse 報文]) とは, |
| [Hasse1] H.Hasse "Bericht über neuere Untersuchungen und Probleme aus der Theorie der algebraischen Zahlkörper. I: Klassenkörpertheorie" Jahresbericht der Deutschen Mathematiker-Vereinigung, Vol.35, 1926, pp.1–55. | |||
| [Hasse2] H.Hasse "――. Teil Ia: Beweise zu I" Jahresbericht der Deutschen Mathematiker-Vereinigung, Vol.36, 1927, pp.233–311. | |||
| [Hasse3] H.Hasse "――. Teil II: Reziprozitätsgesetz" Jahresbericht der Deutschen Mathematiker-Vereinigung, Vol.39, 1930, pp.1-204. | |||
| なる3編の論文を指す. 前者二者 [Hasse1], [Hasse2] は, 貞治の第一論文 [高木13] に関するもので, ハッセ考案による乗法的合同式 ((前出の) 射類\(\,\mathfrak{S}_\mathfrak{m}\,\)の定義で用いた合同式) により類体論の諸定理を証明入りで紹介したものであり, 今後の問題として, |
| ・アーベル拡大の構成問題 (ヒルベルトの第12問題 (既出)) ・\(k\,\)の任意のイデアルはその絶対類体\(\!\:K\!\:\)において単項化すること (単項化定理) の証明 ・\(k_{\!\:i}\,\)を\(\,k_{\!\:i+1}\,\)の絶対類体として, \(k\!=\!k_{{}_{0}}\!\subset\!k_{{}_{1}}\!\subset\!\cdots\! \subset\!k_n\!\subset\!\cdots\,\)は有限で終わるか (類体塔の問題) |
|||
| を挙げている. 一方, 後者 [Hasse3] は, ハッセ独自の記法を用いて相互法則を証明したものである. |
|
\(k\,\)の素点\(\,\mathfrak{p}\), 乗法群\(\,k^{\ast}\!=\!k\!\:\backslash\{0\}\,\)の元\(\,\beta\),
アーベル拡大\(\,K\!\!\:/k\,\)に対し, \(K\,\)は\(\,k\,\)の或るイデアル群\(\,\mathscr{K}\,\)の類体であり,
\(\mathscr{K}\,\)の導手\(\,\mathfrak{f}\,\)の素因子分解を\(\,\mathfrak{p}\,\)に関する部分\(\,\mathfrak{p}^{\nu}\!=\!\mathfrak{f}_{\mathfrak{p}}\,\)を用いて\(\,\mathfrak{p}\!=\!\mathfrak{f}_{\mathfrak{p}}\!\:\mathfrak{f}^{\mathfrak{\!\:p}}\,\)とすれば,\[\beta_{{}_{0}}\equiv\!\beta\:(\mathrm{mod}\,\mathfrak{f}_{\mathfrak{p}}),\:\: \beta_{{}_{0}}\equiv\!1\:(\mathrm{mod}\,\mathfrak{f}^{\mathfrak{\!\:p}})\]なる\(\,\beta_{{}_{0}}\!\in\!k\,\)がとれる. |
|
\((\beta_{{}_{0}}\!\:)\,\)における\(\,\mathfrak{f}_{\mathfrak{p}}\,\)と無縁な成分\(\,\mathfrak{b}\,\)から定まるアルティン記号\(\,\displaystyle{\left(\!\frac{K}{\mathfrak{b}}\!\right)}\,\)を\(\,\displaystyle{\left(\!\frac{\beta,\!\:K\!\!\:/k}{\mathfrak{p}}\!\right)}\,\)と定義し,
積公式\(\,\displaystyle{\prod_{\mathfrak{p}}\! \left(\!\frac{\beta,\,K\!\!\:/k}{\mathfrak{p}}\!\right)\! =\!1}\,\)(\(\mathfrak{p}\,\)は\(\,k\,\)の全ての素イデアルに亘る) を導出した上で相互法則を証明したのであった. |
|
ハッセは, [Hasse 報文] において, 一般相互法則から冪剰余の相互法則も示している. |
|
\(1\,\)の原始\(\,m\,\)乗根を含む代数体\(\,k\:\)および\(\,k\!\:(\sqrt[m\!\:]{\alpha\!\:}\!\:)\,\)で不分岐な素イデアル\(\,\mathfrak{p}\!\in\!k\,\)に対し,\(\,1\,\)の\(\,m\,\)乗根\(\,\displaystyle{\left(\!\frac{\!\:\alpha\!\:}{\mathfrak{p}}\!\right)}\,\)を
\(\displaystyle{\alpha^{\frac{N\!\:\mathfrak{p}\!\:-\!\:1}{\mathfrak{p}}}\!\equiv\! \left(\!\frac{\!\:\alpha\!\:}{\mathfrak{p}}\!\right)\:(\mathrm{mod}\,\mathfrak{p})}\,\)で定義する. |
|
\(k\:\)のイデアル\(\,\mathfrak{a}\!=\!\prod\mathfrak{p}^{\nu}\,\)に対して定義される\(\,k\,\)の\(\textcolor{blue}{\,m\,}\)冪剰余記号\[\textcolor{blue}{\left(\!\frac{\!\:\alpha\!\:}{\mathfrak{p}}\!\right)}= \!\prod\!\left(\!\frac{\!\:\alpha\!\:}{\mathfrak{p}}\!\right)^{\!\!\nu} \!\Longleftrightarrow\left(\!\frac{k\!\:(\sqrt[m\,]{\alpha\,})/k} {\mathfrak{p}}\!\right)\sqrt[m\,]{\alpha\,} =\!\left(\!\frac{\!\:\alpha\!\:}{\mathfrak{p}}\!\right)\sqrt[m\,]{\alpha\,}\]の値は, \(k\!\:(\sqrt[m\,]{\alpha\,}\!\:)/k\,\)に対応するイデアル群\(\,\mathfrak{H}\,\)の\(\,\mathfrak{a}\,\)の属する剰余類のみで決定され, \(k\!\:(\sqrt[m\,]{\alpha\,}\!\:)/k\,\)と\(\,k\!\:(\sqrt[m\,]{\beta\,}\!\:)/k\,\) の導手が互いに素ならば\(\,\displaystyle{\left(\!\frac{\!\:\alpha\!\:}{\beta}\!\right)\!=\!\left(\!\frac{\beta}{\!\:\alpha\!\:} \!\right)}\,\)である. ―― |
|
結局, 貞治の類体論は, 咀嚼吸収度の高い研究意欲旺盛なドイツの若手数学者達によってその価値を見出され, 改良されつつ徐々に広められていったのである.
では, 最初に「類体の構成問題」や「単項化定理」を持ち出したヒルベルトの反応はどうであったか. 『回顧と展望』には |
| ヒルベルトが類體論を讀んだか, 讀まなかつたかハッキリしない. ヒルベルトは, 1898年位から, 例の報文を書いた直後から, 整數論とは離れてゐたのである.
(中略) ところが1925,6年頃に私はヒルベルトから手紙を貰つた. それは私の論文をアンナーレンに轉載することを申込で來たのであつたが, その手紙の中に, ヒルベルトが代數的整數論の講義をするについて,「初めてお前の論文を讀んだ」と書いて, そこの處へ ausführlich と書き入れがしてある. どうも1920年に受取つた論文を25年に初めて讀んだのでは, あまり氣の毒だから,「始めて詳しく讀んだ」ことにしたのであらう. ああ見えても, ヒルベルトは中々細心な所のある人であると思つて, 可笑しかつた. |
|||
| とある. 「アンナーレン」"Mathematische Annalen" とは, [Hilbert2] や [Furtwängler1] などが掲載されたドイツの学術誌である. 講義の題材にしようと考えたくらいであるから, ヒルベルトも貞治の論文を一応は読んだのであろう. しかし, その後, 貞治の論文との関連性においてアルティンやハッセのように目覚ましい活躍を見せた形跡はない. なお,「単項化定理」については, フルトヴェングラーが |
| [Furtwängler5] P.Furtwängler "Beweis des Hauptidealsatzes für die Klassenkörper algebraischer Zahlkörper" Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg, Vol.7, 1930, pp.14-36. | |||
| において (アルティンの相互法則を用いてこれを群論化した上で) 証明しており, これは [Hasse3] でも紹介されている. フルトヴェングラーが持ち出した「類体塔」の問題は, 後年 (1964年), ゴロッド (Evgeny Golod, 1935-2018) およびシャファレヴィチ (Igor Shafarevich, 1923-2017) により否定的に解決された. 次に, |
| [本田6] 本田欣哉『高木貞治の生涯』/ 日本評論社『数学セミナー』1975年6月号, p.52. | |||
| からも少し引用してみよう. |
| フルトヴェングラーのこの成果 (単項化定理の証明) は, 高木の若い弟子弥永昌吉氏によって, 一般の法\(\,\mathfrak{m}\,\)による Strahl 類群 (射類群) 上の類体へと拡張された. やはり1930年のことである. 弥永氏は翌年からヨーロッパに留学して, まずハンブルクでアルチンに師事した. アルチンはちょうど類体論の講義を行なったのであるが, きき手の中に, フランスの青年数学者クロード・シュヴァレイがいた. ある日のこと, シュヴァレイが「類体論の算術的証明ができた」といって, 弥永氏をおどろかせた. (中略) のちに彼はこれをまとめて学位論文とした. (中略) それは高木のあっせんにより, 1933年の東大理学部紀要にのせられた. |
|||
| 彌永昌吉 (1906-2006) は,「旧制大学3年のとき, 高木先生についてこの理論 (類体論) を勉強し, その美しさに打たれた」と |
| [彌永1] 彌永昌吉『類体論とは?』/ 日本評論社『数学セミナー』1975年1月号, p.2. | |||
| において述べている. 「高木先生やアルティンの指導を受けて, それに関するいくらかの仕事もした」と述べる彌永は, フルトヴェングラーが示した「絶対類体 (導手1) の場合」を「一般の導手の場合」に拡張し,『帝国學士院紀事』および『日本数學輯報』等に掲載された初期の論文 |
| [彌永2] S.Iyanaga "Über den Führer eines relativ zyklischen Zahlkörpers" (相対巡回拡大体の導手について) Proc. Imp. Acad. Japan, Vol.5, 1929, pp.108-110. | |||
| [彌永3] S.Iyanaga "Über den allgemeinen Hauptidealsatz" (一般単項イデアル定理について) Jpn. J. Math. Vol.7, 1930, pp.315-333. | |||
| に著した. [彌永2] では合同イデアル類群の導手における素イデアルの冪の代数的な決定を巡回群に適用すること, [彌永3] では射類群に対する類体を考え基礎体の射類体を決定することを, 各々の考察の主題としている. これは後に群論を駆使した代数的手法で整理 (種の法 Geschlechtermoduln によりこの定理を合同イデアル類体の場合にまで拡張) され,『ハンブルク大学数学誌』および (ドイツの純粋応用数学誌)『クレレ誌』に |
| [彌永4] S.Iyanaga "Zum Beweis des Hauptidealsatzes" (一般単項イデアル定理の証明) Abh. Math. Semin. Univ. Hambg. Vol.10, 1934, pp.349-357. | |||
| [彌永5] S.Iyanaga "Zur Theorie der Geschlechtermoduln" (種の法の理論) J. Reine Angew. Math., Vol.171, 1934, pp.12-18. | |||
| として発表された. 彌永自身が後にインタヴュー |
| [岩波数学]『彌永昌吉先生にお話しを伺う』/ 岩波書店『数学』第44巻第4号 (1992年10月), p.355. | |||
| において「僕のしたもっともきれいな仕事」と述べているものである. |
| 類体論の証明における複雑さは, 貞治自身が「今なお紆余曲折を極め, 人をして倦厭の情を起こさしめる」と述べるほどであった. 貞治の手法は「解析的」な\(\,L\,\)関数が用いられていたが, シュヴァレー (Claude Chevalley, 1909-1984) は (\(L\,\)関数を用いず) イデール群による「代数的」な証明を |
| [Chevalley2] C.Chevalley"La theorie du corps de classes" Ann. of Math. Vol.41, No.2, 1940, pp.394-418. | |||
| において示した. 上掲の「弥永氏をおどろかせた」という「算術的証明」は, その時点では完全ではなかったらしい. これに関する彌永自身の述懐を |
| [彌永6] 彌永昌吉『仏蘭西の一数学者 — Claude Chevalley のこと—』/ 日佛會館『日佛文科』新第八輯 (1942年7月), pp.235-244. | |||
| から引用する. |
| 或日シュヴァレーは私に,「類體論の算術的證明が出來た」と云つて驚かせた. 之は當時懸案の大問題で, 多くの學者が考へてゐたが, その緒に就いて居なかつたのである.
シュヴァレーのそのとき得た證明には, 實は未だ一つ難點が殘され, すつかり算術的にはなつて居なかつたのであつたが, 一般の場合を「圓等分體」の場合に歸着させた彼の方法は素晴しく巧妙なものであつた.
彼は之等のことを纏めて These とし, 丁度1932年, チューリッヒの國際數學者會議に列席の爲渡歐された高木貞治先生と識り合ふ等の機縁もあつて, 高木先生の「類體論」が發表されたと雜誌,「東京帝國大學理學部紀要」に發表した. 彼は後年 (1936) になつて「類體論の算術的證明」を完成した. 叉, 所謂「無限次の場合」をも含む類體論の新しい formulation を得, 算術的な, 詳しい證明と共に1940年に至つて公にした. |
|||
| ここ記された「東京帝國大學理學部紀要」(Journal of the Faculty of Science) に「發表」された論文は,『有限体と局所体の類体論』即ち |
| [Chevalley1] C.Chevalley "Sur la théorie du corps de classes dans les corps finis et les corps locaux" J. Fac. Sci. Imp. Univ. Tokyo, Sect.I, 2, 1933, pp.365-476. | |||
| を指す. これは, 緒言および全十章から成る長大な論文である. 不完全であった算術的証明を完成させた上で「1940年に至つて公にした」論文が, 前出の [Chevalley2] であった. [Chevalley2] の内容を簡潔に記すことは困難であるが, 谷山豊 (1927-1958) の表現を借りれば, 次のように纏められる ( [谷山全集] p.213). |
| \(k_{\mathfrak{p}}\,\)の最大アーベル拡大体の\(\,k_{\mathfrak{p}}\,\)上のガロア群は, \(k_{\mathfrak{p}}\,\)の乗法群の,
適当な位相による completion と同型である (中略). \(k\,\)のすべての素イデアル及び無限素点に対する\(\,k_{\mathfrak{p}}\,\)の直積の適当な部分群\(\,J\,\)で, \(J\!=\!J_0\!\times\!J_{\infty}\,\)と分解される. ここで\(\,J_0\,\)は素イデアル\(\,\mathfrak{p}\,\)に対するもので, 位相的には完全に非連結, 一方\(\,J_{\infty}\,\)は無限素点\(\,\mathfrak{p}\,\)によるもので, 何個かの実数体, 複素数体の乗法群の直積と同型である. (中略) \(k\,\)の最大アーベル拡大体のガロア群\(\,\mathfrak{G}\,\)と商群 (イデール群) \(C\!=\!J\!/k^{\ast}\) (\(k^{\ast}\,\)は\(\,k\,\)の乗法群) との関係を考えると, (中略) \(C\,\)には, \(J_{\infty}\,\)に由来する連結成分\(\,D\,\)がある. (中略) \(\,k_{\mathfrak{p}}\,\)の最大アーベル拡大のガロア群 (\(=\!\mathfrak{G}\,\)における,\(\,\mathfrak{p}\,\)の分解群) と\(\,k_{\mathfrak{p}}\,\)に上記の関係があるが, \(\,\mathfrak{p}\,\)が無限素点のときは, \(k_{\mathfrak{p}}\,\)は総実体又は複素数体だから, その最大アーベル拡大体は\(\,k_{\mathfrak{p}}\,\)上1次又は2次で, この次数は, \(k_{\mathfrak{p}}^{\ast}\,\)における連結成分の次数と等しい. そこで商群\(\,C^{\prime}\!=\!C/D\,\)が\(\,\mathfrak{G}\,\)と同型になることが予想されるが, 事実そうであることが証明されている. これが, イデールの言葉による, 類体論の基本定理である. |
|||
| 彌永昌吉は, シュヴァレーの類体論関連の業績を |
| [彌永7] 彌永昌吉『Claude Chevalleyの業績』/ 岩波書店『数学』第15巻第2号 (1963年10月), pp.355-361. | |||
| に詳しく述べている. のみならず, その20年後 (紀寿を迎えんとする直前) にも, やはりシュヴァレーの類体論関連の業績を解説した記事 |
| [彌永8] S.Iyanaga "Travaux de Claude Chevalley sur la theorie du corps de classes: introduction" Jpn. J. Math. Vol.1, 2006, pp.25-85. | |||
| を著して学界の注目を集めたのであった. 貞治の類体論とアルティンによる相互法則とをもって, いわゆる「古典的類体論」は完成したが, その後も, \(p\,\)進数の理論との関連性から局所体上の類体論が創設され, 代数関数体における類体論との類似関係などが発見されるなど, 多方面で華々しい研究成果が現れている. 例えば, 上掲の谷山豊は, 高次元アーベル多様体の等分点による虚数乗法論の拡張を目的として |
| [谷山] Y.Taniyama "Jacobian varieties and number fields", Proceedings of the International Symposium on algebraic number theory, Tokyo-Nikko, 1955, Science Council of Japan, Tokyo, 1956, pp.31-45. | |||
| を著した (この論文は, [谷山全集] pp.57-70 に収録されている). これは, ヒルベルトが1900年にパリ講演で述べた「基礎体を任意の代数体とする類体の構成問題」(「ヒルベルトの23の問題」の中の「第12問題」) に対する一つの方向性を示す研究であり, 総実な代数体上の二次総虚拡大体 (\(\small{C\!M}\,\)体) におけるアーベル拡大の解明に繋がるものであった. 「アアベル体即ち類体」(『代数的整数論』序) なる標語に代表されるように,「古典的類体論」は\(\,k\,\)の素イデアルの\(\,K\!/k\,\)(アーベル拡大の範疇) における素数分解の構造を解明する. これを非アーベル拡大 (\(\mathbb{Q}(\sqrt[3]{2\!\:})\,\)など) に拡張する試み, 即ち「非可換類体論」についても, \(L\,\)関数と保型形式との関連性から多くの成果が得られてはいるものの, 21世紀になって四半世紀を迎えた今年 (2025年, 高木貞治生誕150年) に至るまで, 完全な解決には至っていない. また, \(K\,\)を有限次代数体ではなく有限体上の高い超越次数をもつ関数体へと拡張する試みは,「高次元類体論」の範疇として, やはり多くの綿密な研究が今現在も進められている. この辺りの事情については, |
| [斎藤] 斎藤秀司『高次元類体論の現在』/ 岩波書店『数学』第67巻第3号 (2015年7月), pp.246-270. | |||
| [加藤] 加藤和也『整数論の近年のいくつかの進展をふりかえって』岩波書店『数学』第69巻第4号 (2017年10月), pp.413-428. | |||
| に, 興味深い記事が展開されている. 類体論に一応の区切りをつけた貞治は, その後, 学術的には大きな業績を残していない. [高木全集] に収録されたその後の論文は何れも数ページから十数ページの短いものであるが, 彌永が |
| [彌永9] 彌永昌吉『数学者の世界』岩波書店, 1982, p.10. | |||
| に述べている通り「英知が溢れ, その内容は必ずしも「尖端的」でなくても, いずれも数学の根柢に触れるものがある」. |
| [高木18] T.Takagi "On the law of reciprocity in the cyclotomic corpus" Proc. Phys.-Math. Soc. Japan, Ser.III, Vol.4, 1922, pp.173-182. | |||
| [高木19] T.Takagi "On an algebraic problem related to an analytic theorem of Carathéodory and Fejér and on an allied theorem of Landau" Jap. J. Math. Vol.1, 1924, pp.83-93. | |||
| [高木20] T.Takagi "Note on Fredholm’s determinants" Nagaoka Anniversary Volume, 1925, pp.313-318. | |||
| [高木21] T.Takagi "Remarks on an Algebraic Problem" Jpn. J. Math. Vol.2, 1925, pp.13-17. | |||
| [高木22] T.Takagi "On the mutual reduction of algebraic equations" Proc. Imp. Acad. Japan, Vol.2, 1926, pp.41-42. | |||
| [高木23] T.Takagi "Zur Theorie des Kreiskörpers" J. Reine Angew. Math. Vol.157, 1927, pp.230-238. | |||
| [高木24] T.Takagi "On the theory of indeterminate equations of the second degree in two variables" Bull. Calcutta Math. Soc. Commemoration Vo.20, 1928, pp.59-66. | |||
| [高木25] T.Takagi "Zur Theorie der natürlichen Zahlen" Proc. Imp. Acad. Japan, Vol.7, 1931, pp.29-30. | |||
| [高木26] T.Takagi "Zur Axiomatik der ganzen und der reellen Zahlen" Proc. Imp. Acad. Japan, Vol.21, 1945, pp.111-113. | |||
| [高木18] 『円分体における相互法則について』は類体論の一つの応用成果として『日本數學物理學會記事』に発表され, 偶数次元空間凸領域の性質に基いた [高木19]『カラテオドリ-フェイエールの解析定理に関する代数的問題とランダウによる関連定理について』と, その続編に当たる [高木21] 『代数的問題に関するコメント』は,『日本数學輯報』(Japanese Journal of Mathematics) 創刊号および第2巻に掲載された. また, [高木20] 『フレドホルム行列式に関する注記』は長岡半太郎の退官記念に教え子達が寄稿出版した『東京帝國大學在職25周年記念號』(私家版, 1925)に掲載され, [高木22]『代数方程式の相互還元について』は『帝國學士院紀事』に掲載されたものである. [高木23] 『円分体の理論について』は, [高木18] の成果をクンマーの正則素数問題に適用したもので, やはり『クレレ』誌に発表された. [高木24] 『二変数の二次不定方程式論について』は『カルカッタ数学協会紀要』に掲載されたもので, 二変数二次不定方程式をペル (バースカラ) 方程式へ帰着させる解法を扱っている. また, ペアノとは異なる方法で自然数における結合則と可換則を導出する [高木25] 『自然数論について』およびその続編である [高木26] 『整数と実数の公理について』は『帝国學士院紀事』に発表された. これらは後に『数学雑談』や『数の概念』に纏められることになるものである. 以上に紹介した [高木1] から [高木26] までは, 論文集 [高木全集] に収録されたものである. 実際には, これ以外にも幾つかの (数ページ程度の短い) 論文が存在する. 何れも, 貞治独特の視点をもって書かれた優れたセンスに富んだ珠玉の逸品と言えよう. ~続く~ |
| ©Copyright 2025 SAKATA MASAHIRO. All Rights Reserved. |