| 評論・随筆・記録 Articles | |||
| 名曲50選 The 50 Greatest Pieces of Classical Music ラヴェルを聴く A Listen to Ravel’s Works 《碧の会》随筆 'Ao-no-Kai' Essays パリを歩く A Walk in Paris スティーヴ・ライヒの音楽 Music of Steve Reich 高木貞治と類体論 Takagi Teiji and Class Field Theory |
|||
| 高木貞治と類体論 Takagi Teiji and Class Field Theory |
|||
| 2025年 執筆 | |||
| 目次 | |||
| §1.高木貞治博士記念室 §1-1. はじめに §1-2. 一色小学校時代 §1-3. 岐阜中学校時代 §1-4. 第三高等中学校時代 §2.数学者への修業時代 §2-1. 帝国大学入学 §2-2. 高等代数の洗礼 §2-3. アーベル方程式とガロア群 §2-4. ドイツ留学時代 §2-5.『ガウス数体上のアーベル数体について』 §3.類体論を創設した頃 §3-1. ヒルベルトの類体 §3-2. 東京帝国大学教授就任 §3-3.『相対アーベル体の理論』 §3-4. ストラスブール万国数学者会議 §3-5. 一般冪剰余の相互法則 §3-6. 類体論の算術的証明 §4.著書に見る思想 (1) §4-1.『新撰算術』 §4-2.『新撰代数学』 |
§4-3.『新撰算術講義』 §4-4.『普通教育代数教科書』 §4-5.『広算術教科書』 §4-6.『高等教育代数学』 §4-7.『代数学講義』 §4-8.『初等整数論講義』 §4-9.『解析概論』 §4-10.『代数的整数論』 §5.著書に見る思想 (2) §5-1.『数学雑談』 §5-2.『過渡期の数学』 §5-3.『近世数学史談』 §5-4.『数学小景』 §5-5.『数の概念』 §5-6.『数学の自由性』 §6.教え子達の追想から §6-1. 貞治への評価 §6-2. ビ分のことはビ分でせよ §6-3. アカデミック・コーター §6-4. エッセンシャルとトリビアル §6-5. 貞治のプロフィール |
||
| §1.高木貞治博士記念室 | |||
| §1-1. はじめに | |||
| 岐阜県本巣市の南部に位置する「富有柿センター」内に「高木貞治博士記念室」は存在する. ここには高木貞治の業績や人柄を偲ばせる遺品や遺稿が数多く展示されており, それらは専門家以外の者が見ても極めて興味深い. 殊に彼の自筆稿や遺墨には人間味が色濃く滲み出ており, 何度見ても感慨深いものがある. 多くの書籍に掲載されている彼の写真と併せて, 未踏の数学領域で格闘しつつ一心に研究を突き進めていく貞治の姿に想いを馳せるわけである. |
|||
 高木貞治 (1875-1960) |
|||
| ――上記の書き出しは, 拙稿『西田幾多郎と京都学派』(2001) の冒頭部に倣ったものである. そこで述懐した通り, 哲学者西田幾多郎は, その人物と業績を知るに及んで, 学生時代の私が非常に感化された学者であった. 一方, 数学者高木貞治もまた, その人物と業績から, 学生時代の私が大いに感化された学者であったのである. 小学校高学年から中学校時代にかけて国内外の文学に魅了された私は, 小説家を志すようになった. 固より算数や数学が苦手であった私は, 高校生になると, 小説家への前段階として (多くの小説家の前例に倣って) 国語科教員を目指すようになり, 文科系のクラスに所属した. 当時は, 文科系の国立大学の受験に必要な最小限の数学の知識しか持ち合わせていなかった. そのような私が高木貞治に興味をもったのは, 大学の図書館で『初等整数論講義』を手にした時であった. 代数学の講義で「フェルマーの最終定理」の存在を知り, 興味をもって整数論に関連した書籍を探し始めたのである (その経緯については拙稿『フェルマーの最終定理と未解決問題』(2003) でも簡単に触れている). これを契機として都内の書店や古書店で専門書を渉猟するうち, 私は次第に数学に惹かれるようになった. 所属が教育学部であったことが幸いして, 国語専修から数学専修への編入を認められたのもこの頃の話である. 内容は後述するが,『初等整数論講義』は, 予備知識なしに読める数学書である. その第2版には, 貞治の娘婿である黒田成勝 (1905-1972) による序文 |
|||
| 本書全般の記述, 特に著者自身の創設になる類体論の光輝のもとに, その最も身近かな具体的事例として解説された二次体論の記述は, 読者に強い感銘を与えるものである (後略) | |||
| が記載されている. この文言は印象的であった. 小説家を志していた私には, 文学で読者に感銘を与えることは理解できる. しかし, 数学で読者に感銘を与えるとは? このとき初めて, 数学というものには底知れぬ深い理論体系と魅惑的で美しい芸術的世界が存在することを漠然と感じた. 是非「類体論」なるものを理解したいと思ったわけである. その後の私は, 大学の講義で数学の基礎を学ぶ傍ら,『解析概論』や『代数学講義』などの数学書を繙いた. 併せて,『近世数学史談』や『数学雑談』などの啓蒙書や, 彼の門弟を初めとする種々の学者達による回想や評伝 (後述) を通じて, 貞治の人物や業績に魅了されていったのである. 前置きはこのくらいにしよう. 高木貞治なる人物が, 学者あるいは教育者として同世代や後世に対して如何に多くの影響を与えたか, 本稿では, その生涯と業績を紹介してみようと思う. |
|||
| §1-2. 一色小学校時代 | |||
| 高木貞治は岐阜県の旧大野郡数屋村 (現在の本巣市数屋) の出身である. 誕生したのが1875年4月21日であるから, 今年 (2025年) は貞治の生誕150年に当たる. 貞治は地元の一色小学校と旧制岐阜県尋常中学校 (現在の岐阜県立岐阜高等学校) を卒業し, 京都の第三中学高等学校 (現在の京都大学) に入学するまでこの地で過ごした. 本稿の冒頭で紹介したように, 岐阜県本巣市の南部に位置する「富有柿センター」内に「高木貞治博士記念室」は存在する. 本節では, この「記念室」内にある「展示品」および |
|||
| [本田] 本田欣哉『高木貞治の生涯』/ 日本評論社『数学セミナー』1975年1~6月号. | |||
| における評伝を軸として, まずは貞治の修業時代を見ていくことにしたい. この「記念室」を私が最初に訪れたのは, 1995年の4月であった. 大学を卒業すると同時に, 私は山梨県甲府市内にある私立の中高一貫校に数学科の専任教諭として採用された. そのため, 当時の居宅は甲府市内にあった. 私は, 春休みを利用して車で甲府を発ち, 長野県内の山道を経由して岐阜県へ入ったのである.「記念室」があった場所は, 現在の「富有柿センター」から3kmほど南にかつて存在した本巣郡糸貫町の役場内にある狭い一室であった. そこでは, 貞治の幼少期の揮毫や学生時代のノートなどを, ガラスケース越しではあるが, 初めて間近で見ることができた. 簡潔な評伝と共に一部の展示品の写真が掲載された小冊子 |
|||
| [高橋] 高橋巌『世界数学界 世紀の金字塔 高木貞治先生』高木貞治博士顕彰会, 1979, 全28頁. | |||
| を入手したのも, その時のことである. それから20年以上を経た2018年の9月に, 再び岐阜を訪れた. この年の3月に「記念室」が新装開設されたことを聞きつけたからである. 今度は, 嘗てのような暗くて狭い一室ではなく, 清潔感のある開放的な空間に移り変わっていた. |
|||
 「高木貞治博士記念室」のある「富有柿センター」 |
|||
| 「富有柿センター」には, 特産品の富有柿を加工する農産工研究開発室や柿に関する資料, 陶芸作品を閲覧できる展示ホールなどがある. 建物の3階にある「記念室」には,
貞治の幼少期の写真や揮毫, 愛用の扇子や眼鏡, 胸像や賞状などのほか, 学生時代のノートや雑誌に寄稿した回想録の自筆原稿などが展示されている.
|
|||
 「高木貞治博士記念室」の中の一画 |
|||
| これらの展示品は, 彼に関する評伝や解説記事に掲載された写真ではよく見かけるものである. しかし, 写真で見るのと実物を間近で見るのとでは, 筆遣いや素材の質感などの印象が全く異なる. 彼の多くの教え子達によって伝説化され神格化すらされている感のある貞治であるが, 彼が架空や想像上の人物ではなく, 実在した生身の人間であったことが如実に伝わってくるのである.
|
|||
| 貞治の出生前後は高木家における種々の事情が重なり, 貞治は母親 'つね' とその兄 '勘助' を養父として幼少時代を過ごした. 勤勉な役人であった勘助は貞治の教育には熱心で,
5歳になった貞治を隣家の医師宅で学ばせ, 漢文の素読させたという. 小学校時代の貞治は, 6年の小学校課程 (尋常科4年, 高等科2年) を, 飛び級制度をもって3年間で終えてしまった. その秀才ぶりはよほど周囲の大人たちを驚かせ, 噂を広めさせたのであろう. 当時の地元の新聞 (岐阜日々新聞1886年1月7日付) には, 貞治の「神童」ぶりが報じられているという . 展示品の中では, まず, 貞治が一色小学校時代 (10歳時) に書いた作文『蟻説』が目を引く. 力強い凛とした筆致もさることながら, そこに記された貞治の力強い主張に感嘆させられるのである. |
|||
 『蟻説』―― 10歳の貞治が書いた作文 (1885年) |
|||
| 蟻ハ一小蟲ニシテ其種類甚タ多ク同類數千群ヲナシ毎群蟻王アリテ之ヲ統フ 其粮を運フヤ荷身ニ十倍スト雖衆議蝟集シ詵々爭ハス孜孜怠ラス遂ニ之ヲ其巢ニ運フ 夏日炎々ノ時タリト雖終日怠ラス勉勵シテ粮ヲ求ムルニ從事ス (中略) 夫人怠惰放逸ニシテ後日困難ニ歎ク者往々之レ有リ 其レヲシテ蟻ノ行為ヲ目セシムレバ豈愧スベキノ甚シキニアラスヤ |
|||
| 蟻たちの勤勉なる様子 (その小さな身体を遥かに凌ぐ大きさであっても真夏の炎天下であっても) 倦まず弛まず無心に餌を巣へ運び冬に備える勤勉さを述べ,「人間の場合, 怠惰に過ごして後で嘆く者がしばしば見られるが, 蟻の行為に比べて如何に恥ずべきことであろうか.」と結んでいる. 次に, 小学校時代に描かれた書画も, その精緻な筆遣いに感心させられるものである. |
|||
  鉛筆画デッサン (左) と 書幅「松竹蒼と瑞靄懸」(右) (1885年頃) |
|||
| デッサンの右上に朱書きされた数字は, 教師による評価点であろうか. 書幅は,「松竹が青々と繁り, めでたい靄のかかった朝焼けの中を鶴が軽快に飛んでゆく.
新たに詩句をしたため新年を祝う. すなわちこれ年はじめの最初の句なり.」という, 貞治自身の創作による七言律詩である. |
|||
| §1-3. 岐阜中学校時代 | |||
| 1886年, 11歳で岐阜中学校に進学した貞治は, 飛び級で小学校を卒業したために在校生の中で最年少であった. 年齢にして3歳以上もの差がある他の同級生 (上級生) に対して, 体力では全く勝ち目のなかった貞治であるが, 学業に関しては上級生たちからも一目置かれていたという. 彼らの数学の宿題を貞治が手伝い, 教師が出題した数学の難問を貞治だけは苦もなく解いてみせたからである. 経済的理由から県議会で中学校廃止論が生じた際, 上級生達が暴力も辞さない構えで議員たちを威嚇しに行く一方で, 貞治は「欧米列強を向こうにまわして, 日本は立って行かなければならない. その人材を養う所が中学校である.」と県知事を相手に論じたらしい. 僅か13歳の貞治の説得が効いたらしく, 中学校は廃止を免れたのであった. 彼の意外な一面が窺えるエピソードである. この時代に書かれた論説文や授業ノートも, 筆致および内容の点において目を見張らせるものがある. |
|||
 11歳時の論説文『善ヲ為スコト最モ樂シキノ説』(1886年) |
|||
| 人生ノ最モ快樂トスル所ハ善ヲナスニアリ (中略) 絲竹管絃ノ樂ハ人ノ耳目ヲ快爽ナラシムト雖モ以テ眞ノ樂ミトナスベカラス 然レトモ善ヲナスハ最も自己ノ心ヲ愉快ナラシム善ヲナスコト尤も樂シトハ其之ニアルカ |
|||
| 貞治自身の経験に即した主張なのか, 古人の言を引用したものかは判らない.「善」に関して論じている点では, 本稿の冒頭で触れた西田幾多郎の著作『善の研究』を連想させる. とは言え, この書物が出版されたのは後年 (1911年) のことであるから, その影響で記したものではないであろう. 「動物学」のノートにも, 精密に科類ごとの特徴が記載されている. |
|||
 岐阜尋常中学校時代の「動物学」の授業ノート |
|||
| 袋獸類 此ノ目ニ属スル者ハ腹ノ外ニ袋狀ノ皮ヲ有ス其ノ子ヲ生ムトキハ其ノ袋内ニ於テ哺乳スル者ナリ 袋獸屬 此屬ハ尾太クシテ小キ鱗ヲ蒙レリ此ノ尾ヲ以テ樹枝ニ倒懸シ果實或ハ小動物を食フ其ノ足ノ構造ハ握ルヘキモノニシテ極滑ナル者ト雖モ能クヲ握ル |
|||
| また, 14歳の貞治が認めた『明治廿三年ノ新正ヲ賀ス』も, 当時の貞治の性格や未来への力強い意欲が窺える興味深い資料である. |
|||
 生家に保存されていた『明治廿三年ノ新正ヲ賀ス』(1890年) |
|||
| 光陰矢ノ如ク明治廿二年旣ニ去リ鳳歴茲ニ再ヒ端ヲ開キ明治廿三年ノ春トハナレリ 昨年内ニ起コリシ出来事ヲ回想スレハ恍惚トシテ昨日ノ夢ノ如シ 嗚呼昨年ハ實ニ多忙ノ年ニテアリシ其社會ニ起リシ事ハ有形無形頗ル夛シ 吾人ハ先指ヲ憲法發布ニ屈セントス 憲法旣ニ定マリ我國立憲政體ノ基礎始メテ立チ確トシテ又動カスベカラズ |
|||
| ややペダンティックな趣を否めない表現であるが, いずれは国を背負って立つことを自覚する若々しい気概が感じられる論説であり, 読んでいて微笑ましい. |
|||
| 中学校で用いられたテキストは英語による原書であった. 当時の様子を後年の貞治が記した | |||
| 『中学時代のこと』/ 学校図書株式会社『学図』第1巻第3号 (1952年10月号), pp.2-4. | |||
| の自筆原稿が「記念室」に展示されている. |
|||
 貞治が中学時代を回想した『中学時代のこと』の原稿 (1952年) |
|||
| 最近, 或る機會に, 人から聞かれて, 幼年時代の思い出話をしたときに感じたことは, 老来の健忘, 驚くべき記憶の不確なことであつた. その覚束ない記憶を辿つて, 中学時代の事を少しばかり書いて見よう. (中略) あの頃, 日本語の教科書というものは殆ど無かつたのであろう. 吾々の使つたのは, 全部が, いわゆる「原書」であつた. |
|||
| これらのテキストは特に初級生や2年生には難しかったため, 教師が大意を講義して生徒がそれを筆記し, 問題を解く際にだけテキストを参照していたようである. この時代における貞治の授業ノート (数学) を見てみよう. 「展示室」にあるのは「立体幾何」のノートである. 青で印刷された縦書き用の罫紙に, 一字一句, 丁寧に清書されている. |
|||
 「立體幾何學」の授業ノートと解説パネル |
|||
| 前出の『中学時代のこと』によれば,「(テキストは) トードハンターの小代数, ウィルソンの幾何学を使つた.」とある. 「立体幾何」の授業におけるテキストは, 英国の数学者ウィルソン (James Wilson, 1836-1931) の |
|||
| [Wilson] "Solid Geometry and Conic Sections New Editions" Macmillan, 1882, 全156頁. | |||
| であろう. このテキストでは, 基本的な立体図形や円錐曲線の性質が詳細に解説されているが, 中には, 球面三角形の面積 (p.66) や正多面体におけるポアンカレの双対定理に関する問題 (p.70) , 射影平面上の完全四角形と調和点列 (pp.85-88) など, 現在の中学や高校では扱われない題材も含まれている. ところで, 上掲のノート (展示箇所) の内容は基礎的なもので, |
|||
| 定義二十七 正圓錐体ハ直角三角形カ其直角ヲ作ル 一辺ノ周リニ廻轉シテ生スル体ナリ ABC ヲ直角三角形トシBヲ其直角トス 今此三角形ヲ AB 辺ヲ周リテ廻轉セシムレバ AC ノ痕跡ハ圓錐面ヲナシ BC ハ圓ヲ作ル 此圓ヲ圓錐体ノ底ト云フ |
|||
| と, 貞治自身の翻訳で記されている. これは, [Wilson] pp.43-44 における | |||
| Def. 27. A right circular cone is the solid produced by the revolution of a right-angled triangle round one of the sides containing the right angle. Thus let ABC be a triangle right-angled at B, and let it revolve round AB. Then AC will trace out a conical surface. BC will trace out a circle, which is called the base of the cone. |
|||
| に該当する. 一方, 英国の数学者トドハンター (Isaac Todhunter, 1820-1884) の代数のテキストは, 当時の最新版としては, |
|||
| [Todhunter1] "Algebra for beginners with numerous examples New edition" Macmillan, 1887, 全328頁. [Todhunter2] "Algebra for the Use of Colleges and Schools New edition" Macmillan, 1877, 全608頁. |
|||
| の二種が存在した. 「展示室」にはこの時代のノートが展示されていないため,「小代数」が何れのテキストを指すものかは判断できない. 仮に上掲書の何れか一方が該当するならば, 当時の中学で扱う内容に鑑みて [Todhunter1] と推察されるが, このテキストには, 基礎的な問題のみならず, 現在で言えば, いわゆる難関大学を目指す高校生 (受験生) にも通用し得るような高度な演習問題が散在している. 一方, [Todhunter2] の前半部も現在の中学校や高校で扱われる内容であるから, これが授業のテキストとして用いられた可能性も皆無とは言えない. しかし, その後半部になると, 冪級数展開 (pp.335-343) や連分数展開 (pp.375-387, pp.514-531), 超幾何級数 (pp.511-514) およびその連分数展開への応用 (pp.527-529) など, 現在の大学レヴェルの話題が含まれている. ウィルソンおよびトドハンターの何れのテキストも, 演習問題が豊富で興味深い内容である. しかし, 中学校の授業で扱われるものとしては, その量の膨大さとレヴェルの高さに驚かされるのである. 何れも巻末に演習問題の解が付されてあるが, あくまでも最終解 (略解) のみであり, 末尾にある「他の出版物を宣伝する広告」を見ると, これらの詳細な解答集は別売にされていたことが分かる. |
|||
| ところで,「展示室」には,「14歳の時のもの」と解説パネルに記された (1889年11月27日の日付がある) ノートも展示されている. |
|||
 交代式に関する貞治のノート (1889年) |
|||
| ところが, この内容はトドハンターによる上掲のテキストには存在しない. ノートの「第二 ―― 交代式」の項の冒頭部には, |
|||
| 抑 交代式ナル名稱ハ髙等代數學ニ於テハ旣ニ久シク用ヒ来レル者ナレド, 余輩ハ未タ嘗テ此名稱ヲ初等代數學教科書中ニ見タルコトナシ. 然レドモ, 一通リ, 交代式ノ何タルヲ知ルコトハ, 甚タ容易ニシテ且對稱式トハ最も親密ナル関係ヲ有スルモノナレバ, 旣ニ對稱式ヲ論シタル以上ハ是非トモ交代式ノ何タルヲ詳ニセザルベカラザルナリ. |
|||
| なるやや大袈裟な前置きがある. ここに記された「余輩」が貞治自身を指すものとすれば, より程度の高い他のテキストを繙いた貞治が独自に作成したノートということになるが, 次頁の中ほどには「能ク交代式ノ何タルヲ飮込ミタル讀者ハ容易ニ左ノ定理ヲ發見スルコトヲ得ベシ.」なる一文がある. これにより, これが貞治以外の「読者」を想定したノートなのか何かの原書を正直に翻訳したノートなのか, 判然としなくなるのである. 因みに, 現在の岐阜県立岐阜高等学校に保存されている貞治の成績表 (4年級時) によれば, 漢文97 英語95 代数100 幾何93 化学70 体操77 …… で, 平均86, 席次は22名中1位であったという. |
|||
| §1-4. 第三高等中学校時代 | |||
| 一色小学校と岐阜県尋常中学校を何れも首席で卒業した貞治は, 16歳になる年 (1891年) に, 第三高等中学校 (後の旧制第三高等学校, 京都大学の前身) に入学した. 中学からの推薦により, 無試験であったという. 貞治は, 初めて親元を離れ, 京都での下宿生活を始めたのである. 第三高等中学校時代も, どの科目も熱心に聴講した様子が窺える. 授業のノートは, 青で印刷された縦書き用の罫紙に図や解説が丹念に書き綴られており, 何れも極めて読みやすい. テキストはやはり原書であったらしく, 貞治のノートにも, 本文は縦書きであるが随所に横文字が見られる. 例えば, 細胞, 組織, 果実などが項目別に記載された「植物学」の授業ノートには,「凡テ, 次第ニ生長スル維管束ヲ開出又ハ無限維管束 Open or Indefinite Bundle ト云ヒ, 次第ニ生長セサル者ヲ封鎖又は有限維管束 Closed or Definite ――ト云フ」とある. また,「農学」の授業ノートには, 牛一頭の全体像が描かれ, 番号を附された各部位の名称が整然と記載されている. 事物をつぶさに観察し, それを精確に描く貞治の観察と画力とに感嘆させられるのである. |
|||
  第三高等中学校時代の「植物学」(上) と「農学」(下) の授業ノート |
|||
| 貞治が数学者を志すようになったのは, この第三高等中学校時代であった. 当時の三高には, 帝国大学を卒業して後に京都帝国大学教授となる新進気鋭の数学者河合十太郎 (1965-1945) がいた. 貞治と同様, 貞治と同期の吉江琢兒 (1874-1947), 一級上の林鶴一 (1873-1935) も, 河合の薫陶を受けて数学者を目指すことになるのである. 河合は, ドイツ留学時代にクライン (Felix Christian Klein, 1849-1925) とヴェーバー (Heinrich Martin Weber, 1842-1913) に学んだ関数論の専門家で, |
|||
| [百年史上]『日本の数学100年史 上』岩波書店, 1983, 全337頁. | |||
| によれば,「よく整理された講義をし, (上掲の3名を含む) これらの俊秀に数学への志向を植えつけた.」(p.231) という . 「展示室」には, 河合十太郎の講義を纏めたノートが展示されている. 一つは, 解説パネルに「随感録」と表示された縦書きのノートで,「第三高等中学校当時のものと思われる.」とある. |
|||
 「随感録」と解説パネルにある「代数学」のノート |
|||
| ノートを見ると,「一次方程式ヨリ生スル不合理ノ商」なるタイトルの次に「英国, あいざっくとゞはんたー」なる記述がある. 実際, その内容 | |||
| 凡テ一元一次方程式ハ\(\,ax\!=\!b\,\)ナル形に直スコトヲ得ベシ, 此方程式ヨリ\(\,\displaystyle{x\!=\!\frac{b}{\,a\,}}\)ヲ得. 偖, 若\(\,a\!=\!0\,\)ナルトキハ\(\,x\,\)ノ價ハ\(\,\displaystyle{\frac{b}{\,0\,}}\,\)ナル形ヲナス, 此場合ニ於テハ\(\,x\,\)ニ如何ナル價ヲ與フルモ, 此方程式ニ適合スベカラズ, 其故ハ\(\,x\,\)ニ如何ナル價ヲ附スルトモ, \(ax\!=\!0\,\)トナルヲ以テ, \(0\!=\!b\,\)トナリ, 即チ不合理ナルヲ以テナリ. |
|||
| は, [Todhunter2] p.117 における | |||
| Every equation of the first degree with one unknownquantity may be reduced
to the form \(ax\!=\!b\). Now from this we obtain\(\,\displaystyle{x\!=\!\frac{b}{\,a\,}}\,\). If \(a\!=\!0\) the value of \(x\) takes the form\(\,\displaystyle{\frac{b}{\,0\,}}\,\); in this case no finite value of \(x\) can satisfy the equation, for whatever finite value be assigned to \(x\), since \(ax\!=\!0\), we have \(0\!=\!b\), which is impossible. |
|||
| の忠実な翻訳である. もう一つは横書きの英文によるノートで, 解説パネルには, "Elementary Trigonometry, 1892年",「河合十太郎教授の講義を, 高木博士がまとめたノート」とある. |
|||
 河合十太郎「初等三角法」講義のノート (1892年) |
|||
| ここには二種類の定理が記されている. 一つは,「三角形ABCの垂心をP, 外心をOとして, 辺BC の中点を A'とするとき, AP=2OA'.」であり (下図参照), 簡明な証明が付されている. |
|||
 貞治が描いた九点円 (上掲写真の一部を拡大したもの) |
|||
| 他の一つは, フォイエルバッハの定理の一部「三角形ABCの九点円は内接円に接する」であり, その証明が「この二つの円の中心間の距離がそれらの半径の差に等しい」ことをもって示されている. 貞治のノートの表紙には河合十太郎とトドハンターの名が記載されているが, 現在の我々が目にすることができるトドハンターの著書に "Elementary Trigonometry" なるタイトルは見当たらない. トドハンターによる三角法のテキストは, 当時の最新版としては, |
|||
| [Todhunter3] "Torigonometry for Beginners with numerous examples" Macmillan, 1866, 全228頁. [Todhunter4] "Plane trigonometry for the use of colleges and schools with numerous examples New Edition" Macmillan, 1890, 全341頁. |
|||
| の二種であった. 後者には九点円に関する記述が見られる (pp.276-278) が, 貞治が記したような三角法による詳細な証明は記載されていない. ところで, 澤山勇三郎 (1860-1936) は, |
|||
| [澤山] 森本清吾編『澤山勇三郎全集』岩波書店, 1938, 全310頁. | |||
| においてフォイエルバッハの定理に24通りの証明を与えている (pp.3-25, pp.109-167) が, その中にも貞治と同一の証明法は記載されていない.
最も近い手法を強いて挙げるならば, 第22証明 ([澤山] pp.165-167) であろうか. しかし, これらの証明が『東京數學物理學會記事』(第2期, 1901-1918) に掲載されたのは, 上掲の講義ノートが作られてから10年以上も経過した後のことである. 後年の貞治は, 既に証明された定理であっても貞治自身の創意工夫を加えた手法で著作に纏めることがあった. このノートにもその片鱗が表れているように思う. |
|||
| §2.数学者への修業時代 | |||
| §2-1. 帝国大学入学 | |||
| 第三中学高等学校を優秀な成績で卒業した貞治は, 1894年, 19歳で帝国大学理科大学 (現在の東京大学理学部) に (吉江琢兒, 林鶴一と共に) 入学した. この時も無試験であったという. 当時, 帝大数学科における日本人教授は菊池大麓 (1855-1917) と藤澤利喜太郎 (1861-1933) の二人であった. 菊池はイギリス留学を経て22歳で教授に就任し, そのときの学生であった藤澤利喜太郎がドイツ留学を経た後に教授として加わったのである. |
|||
 菊池大麓 (1855-1917) |
 藤澤利喜太郎 (1861-1933) |
||
| 貞治の帝大時代の状況を, 前出の [本田] および [百年史上] に加え, 貞治自身が学生の頃を回想した講演録『回顧と展望』(東京帝国大学理学部数学談話会, 1940) を援用して概観することにしよう. この時代の貞治自身のノートの存在は確認できないが, 吉江琢兒の当時のノートによれば, 藤澤利喜太郎が担当した解析関係の内容は次のようなものであった ([百年史上] pp.165-166). |
|||
| 【第1,2年】微分積分学 微分法:実数, 極限, \(\varepsilon\)-\(\delta\:\)流の連続関数, テーラー展開, 偏微分, 全微分, 微分幾何初歩, 等. 積分法:定積分, 特異積分, 留数計算, ガンマ関数, ディリクレ積分, ベルヌーイ数, 等. 微分方程式:一階常微分方程式, 特異解, 定係数線形常微分方程式, 全微分方程式, 等. フーリエ展開:ディリクレ条件, フーリエ積分, 変分法初歩, 極小曲面. ルジャンドル微分方程式:ベッセル方程式, 超幾何級数, 全微分方程式の積分条件. 偏微分方程式:一階の場合, シャルピの方法, 二階の場合, 等. |
|||
| 【第2年】楕円関数論 楕円積分, ヤコービの楕円関数, 乗法理論, テータ関数, 変換公式と楕円関数の表示, 等. |
|||
| 【第3年】一般関数論 複素積分とコーシーの定理, 留数計算, 解析接続, アーベル積分とアーベル関数, 代数関数とリーマン面, 等. |
|||
| 現在の大学におけるカリキュラムと比較すると, 講義の順序や内容の点において, 雑多で詰め込み主義的な印象を受ける. |
|||
| また,『回顧と展望』には, 次のような述懐がある. | |||
| 當時何を敎はつたか, 古い記憶を辿つて見ると, 先づ微分積分それから解析幾何學. これは當然だが, 次で二年になると, Durege の楕圓函數論といふものをやつたものである.
これは古い本だから, 諸君は知らないだらうが, まあヤコービの楕圓函數論を書いたもの, つまり Fundamenta Nova の平易な解說といつたものである. 函數論の出來る前の楕圓函數論で, 随分時代離れのものだが, 多分これは, 私の想像なんだけれども, ずつと明治の初期に, ケンブリッヂ邊りから, さういふシステムが輸入されたのではないか ―― と思はれる. それから, サルモンの代數曲線論, 例の略記法か何かで, 吾々はそれが射影幾何學であることを知らずに習つた (後略) |
|||
| ここに現れる「Durege の楕圓函數論」は, デュレージュ (Heinrich Durège, 1821-1893) の |
|||
| [Durège] "Theorie der Elliptischen Functionen Versuch Einer Elementaren Darstellung, Dritte auflage" B.G.Teubner, 1878, 全390頁. | |||
| であると思われる. [百年史上] p.170 に掲載されている1897年当時の東京帝大数学科の蔵書一覧の中に, 楕円関数やアーベル関数論についての著書として "H.Durège
(1878)" なる記載があるからである. これは, 楕円関数を第一種楕円積分の逆関数と看做したヤコビ (Carl Gustav Jacob Jacobi, 1804-1851) の "Fundamenta Nova" 即ち |
|||
| [Jacobi] "Fundamenta nova theoriae functionum ellipticarum" Sumtibus Fratrum, 1829, 全191頁. | |||
| をもとに, 楕円関数の構成とその応用を詳細に解説したものである. 貞治は, 後に複素関数論が発展して楕円関数の二重周期性や解析性から楕円関数を再構成したヴァイエルシュトラス
(Karl Weierstraß, 1815-1897) の手法が一般的になったことに鑑みて, 前者を「時代離れ」と評したのであろう. ところで, 講演録『回顧と展望』は, 後に『近世數學史談』に収録されることになったものである. 『近世數學史談』には, 初版 (共立社書店, 1933), 第2版 (河出書房, 1942年), 第3版 (共立出版, 1970年), 文庫版 (岩波書店, 1995年) が存在するほか,『數學雜談』との合本版 (共立出版, 1946年, 1996年) も存在する. 第3版以降は, 第2版の内容を現代仮名遣いに改めただけであり, 内容としての差異はない. ところが, 実は上掲書の他にも (一般にはほとんど知られていないが) 講演の速記録を活字化した |
|||
| [速記版]『回顧と展望』考へ方研究社「高數硏究」第5卷第4號 (1941年1月), pp.1-6. | |||
| が存在し, ここには, 上掲書とは異なる表現や上掲書では削除されている箇所が含まれている. 以下, 特に必要がない場合 (断りなく『回顧と展望』を引用する場合) は, 第2版を用いることとする. |
|||
 『近世数学史談 2版』(河出書房, 1942) |
|||
| さて, 貞治の言う「ケンブリッヂ邊りから」云々は, 日本人初のケンブリッジ大学の卒業生であった菊池大麓の影響を示唆したものであろう. イギリスで欧米の自由主義的ないし進歩主義的な思想に接した菊池は, 早期のうちに日本を欧米先進国の水準にまで高めようと考えたものと思われる. その菊池大麓は幾何の担当であった. 第一年および第二年では平面と立体の幾何が扱われたという. 小倉金之助 (1885-1962) は |
|||
| [小倉]『小倉金之助全集 第2巻』勁草書房, 1973, 全402頁. | |||
| において, 帝国大学数学科の最初 (第一期生, 1894年) の卒業生であった高橋豊夫 (1861-1944) に当時の教科書に関して尋ねている.
それによれば,「平面解析幾何は教科書を用いなかったが, それはサーモンの『円錐曲線』のような講義であった」という (pp.52-53). 高橋の十数年後に入学した貞治は, 明確に「サルモンの代數曲線論」と述べている. これは, サーモン (George Salmon, 1819-1904) の最新版のテキスト |
|||
| [Salmon1] "A Treatise on Conic Sections 6th edition" Longman, 1879, 全399頁. | |||
| またはその続編に該当する | |||
| [Salmon2] "A treatise on the higher plane curves: intended as a sequel to A treatise on conic sections 3rd edition" Hodges, Foster&Figgis, 1879, 全389頁. | |||
| であろう. [Salmon1] は, 直交座標, 極座標, 行列式による (直線や曲線の) 表記法および射影幾何の手法を用いて, 円錐曲線が有する多くの性質およびその応用が詳細に解説されるテキストである. [Salmon2] は, 斉次座標, 代数曲線の一般的性質 (方程式の項数, 交点と接線, 曲線の描画, 極など), 包絡線, 三次曲線, 四次, 超越曲線, 変換論 (線型変換, 射影変換, クレモナ変換など) が扱われるテキストである. 貞治の言う「略記法」は現在では耳慣れない用語であるが, [速記版] における該当箇所を見ると「サルモンのアブリツジト・ノーテーションを射影幾何とは知らずに習つた」とある. 恐らく "abridged notation" を指すのであろう. この用語の初出となる [Salmon1] の "CHAPTER IV" (p.53) には, |
|||
| Let us call | |||
| \(x\cos\alpha+y\sin\alpha-p,\:\alpha\,;\:\:x\cos\beta+y\sin\beta-p,\:\beta.\) | |||
| Then the theorem just stated may be more briefly expressed ; the equation \(\alpha-k\beta=0\) denotes a line passing through the intersection of the two lines denoted by \(\alpha=0,\:\beta=0\). We shall for brevity call these the lines \(\alpha,\,\beta,\) and their point of intersection the point \(\alpha\beta\). | |||
| とある. ヘッセの標準形を用いた直線束を\(\,\alpha-k\beta=0\,\)と表記するというものである. この記法により, "CHAPTER IX" (pp.201-202) では,「四辺形を作る4直線\(\,\alpha,\beta,\gamma,\delta\,\)に対し, \(\alpha\gamma=k\!\:\!\:\beta\!\:\delta\,\)は, この四辺形の4頂点を通る二次曲線を表す.」なる定理が示される. この表記を用いて初等幾何学における種々の定理を示す手法はなかなか鮮やかであり, 興味深いものがある. 菊池による幾何では, 2次曲線や2次曲面を含めて射影幾何学的に扱われ, 解析幾何ではなかったという. 第2年における平面代数曲線論の講義では, 特異点やプリュッカーの公式, 3次曲線 (楕円曲線) の理論 (不変量など) が扱われたようである ([百年史上] p.166). |
|||
| §2-2. 高等代数の洗礼 | |||
| 『回顧と展望』において, 貞治による学生時代の回顧は次のように続く. |
|||
| 藤澤先生はベルリンでクロネッカーの講義を聽かれたらしいのであつて, 代數を大學へ入れなくてはならぬといふことを絕えず言つてゐられたのであるが,
當時日本では, 代數は中學校でもう卒業してしまつたもののやうに考へられてゐた. そこでその後セミナリが出來てからは, さういふ處で頻りに代數の問題を與へられた. 當時代數といへばセレーの「高等代數」で, それによつて, 私は, アーベル方程式を讀めと言はれ, そこで謂はゆる高等代數の洗禮を受けたわけである. しかし, その當時, 已に書棚の隅つこに, ウエーバーの「代數學」の第1卷が來てゐたので, それを探し出して, ガロアの理論に接したのだが, それが本當に分つたのだかどうだか, その後, 段々いろいろ新しいものが來るやうになつて, ウエーバー第2卷も軈て來た. |
|||
| [本田] によれば,「藤沢はドイツで, 学問としての数学を, 本格的に学び, また '研究する' ということも学んできた」といい,「彼が, 数学のセンスを十分もっていたことは, 1900年のヒルベルトの有名なパリ講演をきいて, それを日本に紹介している文章が, かなり的確にその内容を把握していることからも, よく了解される.」という. 貞治のいう「セミナリ」とは, 第3年の随意科目として藤澤の創設により1893年頃から制度化された「数学研究」([百年史上] p.215) を指すのであろう . 学生ごとに個別に異なる課題が与えられ, 一定期間の後にレポートを提出するものであったという. 藤澤が貞治に「アーベル方程式」を課した経緯は不明であるが, 結果として, これが貞治の数学者としての方向性を決定づけるものとなった. 以下, これに関して少し詳しく述べることにする. 1896年から1900年にかけての5年間に,『藤澤敎授セミナリー演習錄』全5巻が東京数学物理学会から刊行された. 貞治のレポート『あーべる方程式ニツキテ』は, その第2巻 (1897) に収録されている. ここでは, |
|||
| [科学技術史]『日本科学技術史大系 第12巻』第一法規出版, 1969, 全641頁. | |||
| に掲載された記事を援用して貞治のレポートを概観してみよう. 前掲の『演習録』第一巻の緒言において,「セミナリ」および『演習録』の意図を, 藤澤利喜太郎は次のように述べている ([科学技術史] p.108). |
|||
| 余ガ「セミナリー」に於テハ學生諸氏ヲシテ或ル時ハ數學上特別ノ事項ニ就キ調査講窮セシメ或ル時は著名ナル數學大家ノ論文ヲ講讀論評セシメ又或ル時ハ恰好ナル問題ニ就キ自家ノ硏窮ヲ爲サシメ演習ノ方法ハ一ツニ時宜ニ任カス
(中略) 其中ニハ間々貴重ナル材料ナニキシモアラズシテ此儘之ヲ捨ツルノ何ントナク物惜シキ心地セラルヽモノカラニ其中に就キ世ニ裨益スルトコロアラント思ハルヽ二三ノ篇ヲ撰ビ題シテ「セミナリー」演習錄ト名ヅケ東京數學物理學界ニ請ヒ同會ノ出版物トシテ出版スルコトヽセリ |
|||
| 藤澤が貞治に与えた課題は,「アーベル方程式を讀め」であった. 留学中に藤澤自身が目の当たりにした現代数学の一端を貞治に覗かせようとしたものと思われる. |
|||
| 貞治の『あーべる方程式ニツキテ』は, 方程式の代数的可解性に関して報告するものである. その序文には, ガウスによる二項方程式の解法からアーベルが根の間の特殊な関係を見出したこと, ガロアがその理論的裏づけを成し (リューヴィルが世に知らしめ) たことが後にエルミート (Charles Hermite, 1822-1901) やクロネッカー (Leopold
Kronecker, 1823-1891) 達の研究起点となったこと書かれている ([科学技術史] p.109). 興味深いことは, 貞治のレポートが, ガウス (Carl Friedrich Gauß, 1777-1855) からアーベル (Niels Henrik Abel, 1802-1829) やガロア (Évariste Galois, 1811-1832) に至る代数的可解方程式研究に関する客観的な報告に留まらず, 最新の代数学の理論の見地からこれらを捉え直そうする意識が見られることである. 序文は次のように結ばれる. |
|||
| コヽニ叙述セントスルハあーべる方程式ノ解法ニ止マル 而シテコノ叙述ニ於テ余輩ハあーべるノ跡ヲ追ハンヨリハ寧ロ最モ斬新ナル見地ヨリ翻テコノ問題ヲ考察セント欲スルモノナリ. コノ叙述ヲナスニ當リ余輩ハせれー, じょるだんねっとー及ビうぇーべる等ノ書★而モ特ニコノ最後ノオーソリチーニ負フ所甚ダ多カリシコトヲ告白セザルベカラズ. |
|||
| [百年史上] pp.168-169 に記載された1897年当時の東京帝大の蔵書一覧から判断すると,『回顧と展望』で挙げられた「高等代數」とは, セレー (Joseph-Alfred Serret, 1819-1885) による |
|||
| [Serret1] "Cours d'algèbre supérieure I, 4ème édition" Gauthier-Villars, 1877, 全647頁. [Serret2] "Cours d'algèbre supérieure II, 4ème édition" Gauthier-Villars, 1879, 全694頁. |
|||
| であり,「代數學」とは, 先述した (河合十太郎が師事した) ヴェーバーによる | |||
| [Weber1] "Lehrbuch der Algebra I" Braunschweig, 1895, 全653頁. | |||
| であろう. 『回顧と展望』の [速記版] には, |
|||
| セレーの高等代數といふ本がありますが, それが唯一つのもので, それによつて僕にアーベルの方程式をやれといはれました. そんなことで所謂高等代數の洗禮を受けた. その時分, 私は圖書室の書棚を捜すと, 書棚には既にウェーバーの代數第一卷が來て居りそれを捜し出して讀んだのですけれども, 本當には判らなかつたのです. | |||
| という記載がある. 前掲の引用部では「本當に分つたのだかどうだか」であった箇所が, 上掲の引用部では「本當には判らなかつた」となっている. 数学に対して真摯に向き合い, 知ったかぶりをしたり誤魔化したりしない貞治の誠実な人柄がここに垣間見えるであろう. |
|||
 J.A.セレー『高等代数学教程』(1879) |
 H.M.ヴェーバー『代数学教程』(1895) |
||
| 『あーべる方程式ニツキテ』には, 上掲書 [Serret2], [Werber1] に加え, ジョルダン (Camille Jordan, 1838-1922) の |
|||
| [Jordan] "Traité des substitutions et des équations algébriques" Gauthier-Villars, 1870, 全667頁. | |||
| および, ネットー (Eugen Netto, 1846-1919) の | |||
| [Netto1] "The theory of substitutions and its application to algebra" Ann Arbor, Mich., 1892, 全301頁. | |||
| の4書が参考文献 (上記引用部における★) として掲げられている. なお, [Netto1] は | |||
| [Netto2] "Substitutionentheorie und ihre anwendungen auf die algebra" B.G.Teubner, 1882, 全291頁. | |||
| のコール (Frank Cole, 1861-1926) による英訳版であるが, 独語版に対して内容の取捨および各章の配置に変更が見られる.
[百年史上] pp.168-169 における当時の数学科の蔵書一覧には, [Jordan] は記載があるが [Netto1] については記載がない. 無論, [百年史上] に全ての蔵書が記載されているわけではないであろうから, [Netto1] が数学科の図書室に存在しなかったとは断定できない. [Weber1] を読んでみると, [Jordan] と [Netto2] の書名が p.481 の脚注に現れる. 貞治は恐らく, ヴェーバーを読む中でこれらの書物の存在を知ったものと思われる. |
|||
 C.ジョルダン『置換論と代数方程式』(1870) |
 E.ネットー『置換論』(1892) |
||
| 余談であるが, ヴェーバーの『代数学教程』は, 現在では, |
|||
| [Weber2] "Lehrbuch der Algebra II" Braunschweig, 1896, 全784頁. [Weber3] "Lehrbuch der Algebra, III" Braunschweig, 1898, 全726頁. |
|||
| を含めた三部作と看做されているが, [Werber3] は, 先に出版された『楕円関数と代数的数』即ち | |||
| [Weber4] "Elliptische functionen und algebraische zahlen" Braunschweig, 1891, 全504頁. | |||
| の改訂増補版であり, 後から追加されたものである. 実際, [Weber1] および [Weber2] の原書の表紙 (上掲) を見ると "IN ZWEI BÄNDEN" なる記載がある ([Weber3] の表紙にこの記載はない). 貞治が「第2巻も軈て來た」と述べている点に鑑みると,『あーべる方程式ニツキテ』の執筆時点において, 貞治は [Weber2] を読んでいなかった可能性がある (但し, 前述した東京帝大の蔵書一覧には [Weber2] の記載がある). それ以前に出版されていた [Weber4] についてはどうか. この書物については蔵書一覧に記載はない. |
|||
| ところで, 上掲の代数学書に関しては, 今現在に至るまで邦訳版が存在しない. 原書 (英語, 仏語, 独語) である点, 用語や表記法が現代のものとは異なる点, 微に入り細に亘る懇切丁寧な解説が頁数を膨大にさせている点などが,
これらの書をかなり読みづらいものにさせている. 貞治が独習したこれらの専門書の内容を少し覗いてみよう. まず, [Serret1] では, 連分数の一般論, 代数学の基本定理, 連立方程式に関する諸定理, 円分方程式と原始\(\,n\,\)乗根, 代数方程式の解に関する諸定理とその数値的解法, 解と係数の関係, 対称式の基本定理, 有理関数分解, 連立代数方程式における消去理論などが解説される. 次に, [Serret2] では, 合同式の一般論, 平方剰余の相互法則, 原始根とその応用, 素数を法とする多項式の分解および既約性, 素数を含む範囲に関するチェビシェフの不等式, 対称群や共役類に関する一般論, 三次および四次方程式の代数的解法, 円分方程式に関する諸定理, 代数方程式の代数的可解性などが解説される. これらの話題の多くは, 後に『代数学講義』や『初等整数論講義』の中に纏められることになるものである. その中で, 貞治の『あーべる方程式ニツキテ』と緊密な関連性をもつ箇所は [Serret2] の終章である. そこには, ガロアによるメモ『方程式の代数的可解条件に関する覚書』即ち |
|||
| [Galois1] "Mémoire sur les conditions de résolubilité des équations par radicaux" 1831/1846. [Galois2] "Des équations primitives qui sont solubles par radicaux, second mémoire" 1830/1846. |
|||
| の解説 ([Serret2] pp.637-667) と, クロネッカー (前出) による論文『代数的に可解な方程式について』即ち | |||
| [Kronecker1] "Über die algebraisch auflösbaren Gleichungen" Akademie der Wissenschaften zu Berlin., 1853, pp.365–374. | |||
| の全文の (セレー自身による解説や言及をもたない) 独語訳がある. そこにおけるガロアの主旨は「代数的に可解なる条件は, 多項式の任意の根が他の2根の有理関数として表せること」であり, クロネッカーの主旨は 「\(\mathbb{Z}\,\)係数アーベル方程式の根は,1の冪乗根の\(\,\mathbb{Z}\,\)係数有理関数として表せること」であった. また, [Werber1] では, 整関数および有理関数の一般論, 行列の一般論とその応用, 対称式の基本定理, 代数学の基本定理, 線形変換, シュトゥルムおよびブーダン-フーリエの定理, 数値方程式における近似法, 連分数とその応用, 円分方程式と原始合同根, 平方剰余の相互法則, 代数体とガロア群, 置換群と巡回方程式, ラグランジュの分解式, 円分方程式とガウス和, ガウス整数と素因子分解, 方程式の代数的可解性の条件などが解説されている. 上掲書における内容は, 現代では用いられない記号や用語が数多く見られ, 読みづらく理解しがたい箇所が少なくない. すると,『あーべる方程式ニツキテ』における「あーべる方程式」の意味するところも疑わしくなるのであるが, [Werber1] の第15節を見ると, それまでに述べてきた巡回方程式に加え, 次のような記述が現れる. |
|||
| Eine irreducible Gleichung \(\varphi(x)\!=\!0\) mit commutativ er Gruppe ist eine Abel'sche Gleichung. | |||
| 即ち, ヴェーバーはガロア群が可換群となる既約方程式も含めてアーベル方程式と称していることが分かる (p.535). これは, 現今の定義と一致するものであるから, 貞治もこの意味で「あーべる方程式」を用いていたと考えてよいであろう. 貞治にとっての肝要部分は, 代数的可解方程式に関する部分であった. 貞治は, 上掲書を繙くことにより, 中学や高校で習ってきたような数式計算を中心とする初等代数ではなく, それらを含有する代数的構造を解明する「高等代數」の「洗禮を受けた」わけである. [Jordan] では, 合同式や平方剰余に触れた後, 直ちに置換の一般論に移り, 一般方程式論へと続く. 内容は [Werber1] よりもやや進んでおり, \(n\,(\geq\!5)\,\)次方程式の代数的非可解性に留まらず, 五次方程式の超越的解法が紹介されている (pp.372-375). 五次モジュラー方程式を用いるエルミート (前出) の手法と, ヤコビの楕円関数を用いるクロネッカーおよびブリオッシ (Francesco Brioschi, 1824-1897) の手法が比較でき, 大変に興味深い. また, [Netto] では, 前半部は, 冪和や判別式を含む対称式の一般論から始まり, \(p^{\!\:k}\,\)次対称群, 群作用, メタ巡回群など, 方程式の代数的可解性を論じるのに必要な概念が解説される. 後半部は, \(n\,(\leq\!4)\,\)次方程式, アーベル方程式, ガロア方程式, 素数冪次方程式の代数的可解性を中心に解説される. |
|||
| §2-3. アーベル方程式とガロア群 | |||
| さて, 貞治による『あーべる方程式ニツキテ』を見てみよう. これは, 序文を除いて全13節で構成され, |
|||
| 第一節 體 第二節 體ノ中ノ函數 第三節 代數體 第四節 正體トがろあノ分解式 第五節 がろあ群 第六節 群ノ移動性ト方程式ノ分解性トノ關係 第七節 群ニ關スル定理 第八節 根ノ有理式 第九節 分解式ノ簡約 第十節 あーべる方程式 第十一節 あーべる方程式ヲ循環方程式ニ歸セシメ得ベキコト 第十二節 循環方程式ノ解法 第十三節 結論 |
|||
| から成る67頁に及ぶレポートである. オリジナルの論文ではないが, ガロア理論をわが国に最初に紹介したレポートとして記憶されるべきものである. その肝要部分である第5節「がろあ群」の冒頭部を見てみよう. |
|||
| \(\varOmega\,(\rho)\,\)ヲ\(\,\mu\,\)次ノ正體\(\,g\,(t)\!=\!0\,\)ヲ\(\,\rho\,\)ノ適合スル\(\,\mu\,\)次ノ旣約方程式\(\,\rho\,,\,\rho_{{}_{1}}\,,\,\cdots,\,\rho_{\mu-1}\,\)ヲ\(\,\rho\,\)ト共軛ナル數トス サスレハ正體ノ定義ニヨリテコレラノ共軛數ハ皆\(\,\varOmega\,(\rho)\,\)ニ屬スルカユヘニ |
|||
| \(\rho_{{}_{1}}\!=\!\theta_{{}_{1}}\!\:(\rho),\,\cdots,\, \rho_{\mu-1}\!=\!\theta_{\mu-1}(\rho)\) |
|||
| ト書くコトヲ得. コヽニ\(\,\theta_{{}_{1}}\,,\,\cdots,\,\theta_{\mu-1}\,\)ハ\(\,\varOmega\!\:\)ノ中ナル\(\,\mu\!-\!1\,\)次以下ノ整式ナリトス. サテ\(\,\omega\,\)ヲ\(\,\varOmega\!\:(\rho)\,\)ノ中ノ一數トセハコレト共軛ナル數ヲ次ノ如ク表ハスコトヲ得. |
|||
| \(\omega\!=\!\varphi\!\:(\rho),\,\omega_{{}_{1}}\!=\!\varphi\!\:(\rho_{{}_{1}}\!\:), \,\cdots,\,\omega_{\mu-1}\!=\!\varphi\!\:(\rho_{\mu-1})\) |
|||
| \(\varphi\,\)モ亦\(\,\varOmega\!\:\)ノ中ナル\(\,\mu\!-\!1\,\)次以下ノ整式ナリトス. 叉逆ニ\(\,\psi\,\)ヲ以テ\(\,\varOmega\!\:\)ノ中ノ有理函數ヲ表ハスモノトセハ | |||
| \(\psi\!\:(\rho),\,\psi\!\:(\rho_{{}_{1}}\!\:),\,\cdots,\,\psi\!\:(\rho_{\mu-1})\) | |||
| ハ共軛數ナルコトハ明カナリ. | |||
| 上記における「正體」は聞き慣れない用語であるが, 前後の文脈から「正規拡大」を指すものと思われる. 以後, 先述したセレーのテキストにおけるガロアの主旨が解説されるのであるが, この節の叙述は, ヴェーバー [Weber1] の pp.467-478 に記載されている |
|||
| §146 "Die Substitutionen eines Normalkörpers." (正規拡大の置換) §147 "Zusammensetzung der Substitutionen." (置換の構成) §148 "Permutationsgruppen." (置換群) §149 "Galois'sche Gruppe." (ガロア群) |
|||
| の翻訳と言ってよい. 一方, 群の (現代とは異なる) 定義を補足したり, 記号の書き換えや置換演算に関する説明の割愛したり, 叙述の方法や順序を改良したりなど, 貞治自身による工夫も随所に施されている. |
|||
| この節の後半部では, 次のように要約される. | |||
| 今\(\,n\,\)個ノ根ノ有理式アランニコレラノ根ノ間ニ一ノ置換ヲ施コストキコノ有理式ハソノ値ヲ變セサルトキハコノ有理式ハコノ置換ヲ許スモノト做スシカスルトキハ \((\mathrm{I})\) \(F(x)\,\)ノ\(\,m\,\)個ノ根ノ間ニ成立スル所ノ\(\,\varOmega\!\:\)ノ中ノ有理的等式ニがろあ群ノ置換ヲ施コシテ得タル結果ハ仍ホ正當ノ等式タルヲ失ハス \((\mathrm{II})\) \(F(x)\,\)ノ\(\,m\,\)個ノ根ノ有理式ニシテがろあ群ノスヘテノ置換ヲ許スモノハ\(\,\varOmega\!\:\)ノ中ノ數ナリ. |
|||
| その後, それ以前に提示した4つの定理を根拠にこれらを証明し, この節は閉じられるのである. 先述した通り,『あーべる方程式ニツキテ』は貞治のオリジナルの論文ではない. このレポートは, 全編に亘って, [Werber1] における主要部分 |
|||
| §139-§151 "Die Galois'sehe Theorie." (ガロア理論) §152-§158 "Anwendung der Permutationsgruppen auf Gleichungen." (置換群の方程式への応用) §159-§165 "Cyklisehe Gleichungen." (巡回方程式) |
|||
| を, 貞治自身が咀嚼吸収して纏めたものになっている. 貞治は, 上掲のテキストによって初めて「ガロア理論に接した」のであった. 自身は「本當に分つたのだかどうだか」あるいは「本當には判らなかつた」( [速記版]) と謙遜しているが, セレーやヴェーバーの著書を含め, 記号, 用語, 理論体系が不統一であった時代に, 上掲書のような大部の原書を読みこなす作業は尋常の努力では済まなかったはずである. 仮に, [Weber2] における群論関係の記述と, 私が学生時代に繙いたような代数学書 (例えば |
|||
| [永田] 永田雅宜『可換体論 新版』裳華房, 1985, 全272頁. | |||
| など) のそれとを比較してみれば, 後者の方が遥かに簡単明瞭に書かれていることが理解されるであろう. 藤澤利喜太郎も貞治の非凡なる努力と才能を認めていたのであろう. 貞治のレポートを収録した (前掲の)『演習録』第二巻の緒言には, |
|||
| 高木貞治氏ノ記述ニ係ハル第三ノ論文ハあーべる方程式ヲ論ズルモノニシテ論文ノ事實ヨリ推ストキハ第一冊掲載ノ諸論文ニ攝續スルモノナリ 而シテ高木氏ハ余ガ最初與ヘタル問題ヨリ一層一般ニ卽代數學最近發達ノ眞相ヨリシテあーべる方程式ヲ講窮セラレタルガ故ニ氏ノ論文ハ最モ新ラシキ代數學ノ要領ヲ得ルニ最モ便利ナルベシ. 此緒言ヲ終フルニ臨ミ特ニ一言シタキコトアリ, ソハ本冊の記述者タル三氏ガ何レモ余ガ與ヘタル問題ニ就キ叮嚀ニシテ周密ナル講窮ヲナシ能ク悟ル可キモ語ル可カラザル的ノ妙所ヲ觀破シ, 講窮ノ結果ヲ記述スルニ當リテハ其順序體裁ノ頗ル宜シキヲ得タルコトナリ. |
|||
| とあり, 貞治に対する惜しみない讃辞を与えている. ここで, 藤澤の言う「第一冊掲載ノ諸論文」とは, |
|||
| ・奥田竹三郎『三次方程式四次方程式ノ解法及方程式ノ根ノ有理式ニ付テ』 ・渡辺庸『五次及五次以上ノ方程式ハ一般ニ係數ノ代數式ヲ以テ解クコト能ハザル事ノ證明』 ・吉田好九郎『一變數ヲ含ム有理整數代數函數ハ必ズ一次若シクハ二次ノ實因數ニ分括セラレ得ルト云フ定理ノがうすノ正確ナル證明』 |
|||
| を指し,「本冊ノ記述者タル三氏」とは, 貞治および前出の吉江琢兒と林鶴一を指す. なお,『演習録』第二巻に掲載された吉江と林のレポートは |
|||
| ・吉江琢兒『似眞寫影』(等角写像) ・林鶴一『\(e\,\)及ビ\(\,\pi\,\)ノ超越ニ就テ』 |
|||
| であり,「第三ノ論文」が貞治の『あーべる方程式ニツキテ』であった ([科学技術史] p.93). ここで, 貞治が「軈て來た」と述べる「ウェーバーの第2卷」すなわち [Weber2] を見てみよう. まずは群論の基礎から始まる. 有限アーベル群の指標, 円分体のガロア群, アーベル方程式, 有限群におけるシローの定理, フロベニウス群など. 次に線形群論が続く. 行列論, 置換論, 有限群の不変式, ヒルベルトの基底定理, 直交群, 回転群, 対称群, 合同群など, 後の議論に必要な概念が準備される. 続いて応用理論が展開される. メタ巡回方程式, 代数的可解方程式に関するアーベルの定理, 三次および四次曲線論 (特に二重接線とガロア群), 五次方程式論 (特に正二十面体と超越的可解性) などが解説されるのである. その後, [Weber2] の主要部である代数的整数論に入る. 代数的整数に関する基本用語と性質, イデアルの素因子分解, 代数体の判別式および共軛差積, (凸体の格子点に関する) ミンコフスキの定理の代数体への応用, デデキントの判別定理, 二次体論および円分体論が展開される. 貞治は恐らくここで初めて代数的整数論に接したものと思われる. 無論, 講義による習得ではない. 自ら専門書を繙き, 精密に読み込み, 緻密によく考え, 根気強く独学を続けたことで, (当時における) 最先端の数学を咀嚼吸収していったのである. さて, [Weber2] 後半部, §179 (p.648) において, クロネッカーによる命題 |
|||
| Alle im absoluten Rationalitätsbereich Abel'schen Zahlkörper sind Kreistheilungskörper. | |||
| 即ち「\(\mathbb{Q}\,\)の任意の有限アーベル拡大は円分体である」が現れる. これは, 後年の貞治を第一級の数学者へと押し上げる契機となった重要な定理と言ってよい. この命題はやがて「クロネッカーの青春の夢」へと拡張され, それは貞治が後に類体論を構築することにより肯定的に解決されることになるからである. これについては次節で詳しく述べることにしよう. |
|||
| さて, 1897年に大学を卒業した貞治は, 大学院生として引き続き東京帝大に在籍した. 『回顧と展望』によれば, |
|||
| その間にいろいろな本を讀んだのであるが, 指導者なしの亂讀で, 本當に讀んだと謂ふよりは, 圖書室にあるだけの本を見境ひもなく片つ端からひつ繰り返して見たといふ程のことであつた. | |||
| ということであり, 分野を限定することなく, 種々の数学書に目を通していたらしい. [百年史上] pp.170-171 には, 東京帝大数学科図書室に残されている図書貸出簿に関する記載がある. 大学3年間と大学院1年間の計4年間で, 貞治は延べ70冊の書物を借り出しているという. そこには, 前出のセレー, ヴェーバーのみならず, 以下の数学書が列挙されている. まず, ディリクレ (Peter Gustav Lejeune Dirichlet, 1805-1859) やデデキント (Richard Dedekind, 1831-1916) の整数論 (講義) |
|||
| [Dirichlet] "Vorlesungen über Zahlentheorie" Braunschweig, 1863, 全414頁. [Dedekind] "Vorlesungen über Zahlentheorie" Braunschweig, 1871, 全497頁. |
|||
| であり, 次にヒルベルト (David Hilbert, 1862-1943) の整数論報告 | |||
| [Hilbert 報文] "Die Theorie der algebraischen Zahlkörper" Jahresb. Deutsch. Math. Verein Vol.4, 1897. | |||
| のほか,「楕円関数についての多くの古典」とある. これらに関して具体的な書名の記載はないが, 恐らく前出のヤコビやデュレージュなどであろう. さらに, クライン (前出) の二十面体論 |
|||
| [Klein] "Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade" B.G. Teubner, 1884, 全260頁. | |||
| や, ジョルダンやピカール (Émile Picard, 1856-1941) の解析教程 | |||
| [Jordan1] "Cours d'analyse de l'École polytechnique I" Gauthier-Villars, 1893, 全613頁. [Jordan2] "Cours d'analyse de l'École polytechnique II" Gauthier-Villars, 1893, 全627頁. [Jordan3] "Cours d'analyse de l'École polytechnique III" Gauthier-Villars, 1893, 全542頁. [Picard] "Traité d'analyse" Gauthier-Villars, 1891, 全457頁. |
|||
| などが挙げられている. |
|||
| §2-4. ドイツ留学時代 | |||
| 貞治が大学院生として在籍した期間は一年足らずであった.「官費留学生」として「數學研窮ノタメ滿3ヶ年獨國留學ヲ命ズ」という辞令を受けたからである. 1898年6月末に大学院を退学した貞治は, 同年8月末にドイツへと向かったのであった. 引き続き『回顧と展望』から引用する. |
|||
| 「洋行」は嬉しかつたが, (中略) 何分數學といへば獨逸, 獨逸といへばベルリンと言はれてゐた時代で, そこへ素養もなく, 自信もない, 東洋の田舍者が飛び込んで行くのだから,
怖かつた. (中略) 1900年に私はゲッチンゲン大學へ參りました. (中略) 獨逸は勿論, 世界各國の大學からの, 言はば選り拔きの少壮學士の集合で實際, 數學世界の中心であつた. そこで私ははじめて, 二十五にも成つて, 數學の現狀に後るること正に五十年, といふやうなことを痛感致しました. |
|||
| 文部省がいかなる理由で貞治の「數學研窮」の場を「獨國」と定めたのか, 詳細は不明である. とは言え, 当時の文部大臣外山正一 (1848-1900) は嘗て菊池大麓と共に教授を務めた仲であり, 1897年には菊池が大学を辞して文部次官に就任した事情に鑑みれば, 貞治のドイツ留学は菊池と藤澤の推薦によるものと考えてよいであろう. ドイツでは, 貞治はまずベルリン大学 Universität zu Berlin (現在のベルリン・フンボルト大学) に留学した. 嘗ては, 北里柴三郎 (1853-1931, 微生物学), 高橋順太郎 (1856-1920, 医学), 森鴎外 (1862-1922, 医学) なども留学していた大学である. そこでは, ヴァイエルシュトラス (前出), クロネッカー (前出), クンマー (Ernst Eduard Kummer, 1810-1893) の全盛期が過ぎ, フックス (Lazarus Fuchs, 1833-1902), シュヴァルツ (Hermann Amandus Schwarz, 1843-1921) などが後を継いでいたという. その中でも貞治が影響を受けた数学者は, 若手のフロベニウス (Ferdinand Georg Frobenius, 1849-1917) であった. 彼による整数論やガロア理論の講義は, 講義用のノートも持たずにキビキビとした活きた講義であったという. 但し, 自身の研究 (群の表現論における指標理論など) を学生や留学生たちを相手に講義することはなかったらしい. 洋行直前の貞治は, ドイツから帰朝したばかりの少壮理学者にフロベニウスの怖さを吹聴されたが, 留学時には数学に対する教訓を与えられたと, 次のように述懐している. |
|||
| 「君, フロベニウスの處へ行くなら餘程注意しなければいかぬ」といふのである. それはフロベニウスが學部長かなんかに成つたときに就任演說をやつた,
その時に, ドイツの科學の進歩を大いに自讚したわけである. それで外國人が頻りにドイツへ科學を勉強しに來る. アメリカからも來れば, 何處からも來る.
近頃は日本人すら來る. 今に猿も來るだろう (中略). しかし實際行つて見ると, そんな怖いこともなかつた. 私が何かある問題を持つて, 先生に訊きに行つたことがあつたが, その時先生は, それは面白い, 自分でよく考へなさい, Denken Sie nach! といつていろいろな別刷などを貸してくれた. この「自分で考へなさい」も, 思へば生れて始めての敎訓であつた. |
|||
| 上記のフロベニウスの逸話を伝えた少壮理学者の名前を, 貞治自身は挙げていない. 当時ドイツから帰国したばかりの教授でベルリン留学生と言えば, 長岡半太郎 (1865-1950, 物理学) または大森房吉 (1868-1923, 地震学)であるが, 前者である可能性が高い. [百年史上] (p.183) に掲載されているドイツ留学生で東京帝大の数学関係者は (前出の) 吉江琢兒と中川銓吉 (1876-1942) であるが, 彼らの渡欧出発は貞治よりも後のことである. |
|||
| [森川] 森川潤『明治期のドイツ留学生』雄松堂出版, 2009, 全303頁. | |||
| には, 長岡が明治25年 (1892年) に渡独して, 明治29年 (1896年) に帝大教授に就任したことが記録されている (p.98). 留学先は, フロベニウスの所属するベルリン大学である (p.180). また, 貞治の後年のエッセイ |
|||
| 『明治の先生がた』/ 鈴木信太郎編『赤門教授らくがき帖』鱒書房, 1950, pp.111-118. | |||
| には, 貞治が大学で長岡半太郎に教わったこと, 貞治の洋行出発時には長岡が横浜港まで見送りに来てくれたこと, ベルリン留学時代の話をいろいろと長岡から聞いたことなどが記されている.
この著書の中で貞治が「長岡さん」と呼んでいることからも, 貞治と長岡との親しい関係性が窺われる. ベルリンにおける講義の内容は, セレーやヴェーバーの著書を通じて留学前に知り得ていたことが大半であったのであろう. 貞治は「大してこれといふこともなかつた」と述べる一方で,「語學の練習とかに時間を費やさざるを得なかつた」とも述べている. 実際, [本田] によれば, 貞治は当時ドイツで盛んであった演劇を好み,「語学の勉強のためと称して」よく観劇に出かけていたらしい. 王立オペラハウス (Königliche Oper), レッシング劇場 (The Lessing Theatre), ゲーテ劇場 (Goethe-Theater) など, ベルリン市内だけでも20の劇場があったという. |
|||
 F.G.フロベニウス (1849-1917) |
 D.ヒルベルト (1862-1943) |
||
| その後, 1990年の春に, 貞治はヒルベルト (David Hilbert, 1862-1943) のいるゲッティゲン大学 (Georg-August-Universität Göttingen) へと移った. この大学には, 貞治より10ほど後に本多光太郎 (1870-1954, 工学) が, 20年ほど後に仁科芳雄 (1890-1951, 物理学) が留学することになる. |
|||
| 一年半の間ゲッチンゲンの雰圍氣の中に棲息してゐる裡に何時とはなく五十年の乘り遲れが解消したやうな氣分になりました. 雰圍氣といふものは大切なものであります. | |||
| ゲッティンゲン大学は, 当時「數學世界の中心」であったが, 貞治はそこでも数学的には関して得るものは少なかったらしい. 無論, 何も得なかったわけではあるまい. 多くの数学書を繙き, 教授達や周囲の学生達と数学に関連した議論を交わす機会も多かったに違いない. とはいえ, 貞治にとってのドイツ留学は, 留学前までに自国で培ってきた数学的素養に対して自信を取り戻したのみならず, 今後は時代を先取りして数学界を牽引しようとする新たな気概まで生じさせる結果となったように思われるのである. |
|||
| 『回顧と展望』の中で, 貞治はヒルベルトとの遣り取りを次のように述べている. | |||
| 「お前は代數體の整數論をやるといふが, 本當にやる積りか?」とえらく懐疑の眼を以て見られた. (中略) 私のやらうといふのは, 例の「クロネッカーの靑春の夢」と謂はれるものの中で,「基礎のフィールドがガウスの數體である場合, つまりレムニスケート函數の虚數乘法をやらう」と思ふと言つたら,「それはいいだらう」といはれ, … (後略) |
|||
| 『回顧と展望』[速記版] には,「フロベニウスは日本人とアツフエを同じに考へてゐる. その原因はフロベニウスの息子が日本人の友達と附合ふので, フロベニウスの伜の所に來るあの男のやうなものであると思つてゐる」とある (「アツフエ」は "Affe" 即ち「猿」を意味する). フロベニウスの先入観はやや大袈裟であるにしても, ガウス以来, クンマー, ディリクレ, デデキントなどへ継承され, 代数的整数論を華やかに展開してきた当時のドイツ数学界には, 東洋の彼方からやって来る日本人たちを見下すような雰囲気が少なからずあったものと思われる. ヒルベルトから見れば, 極東から来た留学生の数学的学力がどの程度のものなのか怪しかったのであろう. この遣り取りが行われた時期と前後して (1900年8月), ヒルベルトはパリ講演 (第2回国際数学者会議) で, この問題の拡張について (「ヒルベルトの23の問題」の中の「第12問題」として) 言及している. 先述した ([Weber2] p.648 に現れた命題) クロネッカー・ヴェーバーの定理は, \(\mathbb{Q}\,\)を基礎体とする類体の構成問題である. ヒルベルトは, 基礎体を任意の代数体とする類体の構成問題の可能性について述べたのであった. 貞治が「やらう」としたのは, 基礎体\(\,K\!\:\)を虚二次体とする場合である. 楕円関数\(\,f(u)\,\)が虚数乗法をもつ (即ち\(\,\tau\!=\!\omega_{{}_{\!\!\:2}}/\omega_{{}_{\!\!\:1}}\!\in\!K\:\)(但し\(\,\omega_{{}_{\!\!\:1}},\,\omega_{{}_{\!\!\:2}}\,\)は\(\,f(u)\,\)の周期, 且つ\(\,\mathrm{Im}\!\:\tau\!>\!0\)) ならば任意の\(\,\mu\!\in\!K\,\)について\(\,f(\mu u)\,\)と\(\,f(u)\,\)に代数的関係がある) とき, 楕円モデュラー関数ないし\(\,j\,\)不変量\(\,j\!\:(\tau)\,\)は\(\,K\,\)におけるアーベル方程式の根であり, \(\,f(u)\,\)の周期等分点\(\,u\!=\!(\mathbb{Z}\!\:\omega_{{}_{\!\!\:1}}\!+\!\!\:\mathbb{Z} \!\:\omega_{{}_{\!\!\:2}})/n\,\)に対するヤコビの関数\(\,\mathrm{sn}\,u\,\)は\(\,K\!\:(\!\:j\!\:(\tau))\,\)におけるアーベル方程式の根である. 逆に, 虚二次体\(\,K\!\:\)上の任意のアーベル体が, \(\,j\,\)不変量, 周期等分値により得られ, (前述した) クロネッカーの構成法 (\(\mathbb{Q}\,\)の最大アーベル拡大\(\,\mathbb{Q}^{\mathrm{\!\:ab}}\,\)が\(\,\mathbb{Q}\,\)に\(\,\zeta_{{\!\:}_{n}}\!=\!e^{2\pi i/n}\,\)を全て添加することにより得られる) と同様の構成法を\(\,K\!\:\)上に見出すこと――これが「クロネッカーの青春の夢」であった. 「青春の夢」(liebster Jugendtraum) なる名称は, ヘンゼル (Kurt Hensel, 1861-1941) の編纂による『クロネッカー全集 第5巻』即ち |
|||
| [Kronecker2] "Leopold Kronecker's Werke Fünfter Band" B.G. Teubner, 1931. 全527頁. | |||
| において, 第27章におけるデデキント宛の書簡 (1880年3月15日付) の冒頭部 (p.455) に現れる. |
|||
| … dass ich heute die letzte von vielen Schwierigkeiten besiegt zu haben
glaube, die dem Abschlüsse einer Untersuchung, mit der ich mich in den
letzten Monaten wieder eingehender beschäftigt habe, noch entgegenstanden.
Es handelt sich um meinen liebsten Jugendtraum, nämlich um den Nachweis, dass die Abel’schen Gleichungen mit Quadratwurzeln rationaler Zahlen durch die Transformations - Gleichungen elliptischer Functionen mit singulären Moduln grade so erschöpft werden, wie die ganzzahligen Abel'schen Gleichungen durch die Kreistheilungsgleichungen. |
|||
| 「この数ヶ月間に亘る困難な研究を克服したと確信している. \(\mathbb{Z}\,\)上のアーベル方程式の根が悉く円分方程式により得られるのと同様,
虚二次体\(\,k\,\)上のアーベル方程式は\(\,k\,\)を虚数乗法にもつ楕円関数の特異モデュライと周期等分点により悉く得られることを証明すること――それは私のお気に入りの若き日の夢だ.」 貞治は, [Hilbert 報文] を通じて, この命題を既に知っていたのであろう. ゲッティンゲンで過ごす間に, 自己の数学的能力に対する自信と矜持を取り戻し, この未解決の問題に取り組む意気込みが芽生えたものと思われる. ところが, ヒルベルトは, 貞治の研究方針について「それはいいだらう」と言ったのみで, 特に何か有益な情報を与えてくれたわけではなかったらしい. フロベニウスから得た教訓「自分で考へ」ることを通じて, 貞治は独りでこの問題に取り組んだのである. |
|||
| §2-5.『ガウス数体上のアーベル数体について』 | |||
| 『回顧と展望』において, 貞治は次のように述べる. |
|||
| ヒルベルト自身は, 私が行きました頃は, 整數論から離れてしまつた後で, (中略) ヒルベルトの側にゐたけれども, 直接には何等の指導も受けなかつた. (中略) しかし, 例のレムニスケートの一件だけは, 幼ないものだけれども, 論文を書いてヒルベルトに見せておきました. ヒルベルトはそれをドクトル論文と思つてゐたやうだが, 當時日本にも相當矜持が出來て, 留學生が獨逸のドクトルを取つて來る必要はないといつた時勢になつてゐたから, 私もその論文を持つて歸つて, これを以て學位を頂戴したわけだが, 獨逸土產といへば, まあそれ位のものであつた. |
|||
| ここにおける「レムニスケートの一件」あるいは「獨逸土產」とされる貞治の学位論文 |
|||
| [高木6] "Ueber die im Bereiche der rationalen complexen Zahlen Abel'schen Zahlkörper" (ガウス数体上のアーベル数体について) J. Coll. Sci. Imp. Univ. Tokyo, Vol.19, Art.8, 1903, pp.1-42. | |||
| は, 帰国後に『東京帝國大學紀要 理硏 XIX』に掲載された. 序文および全15節から成る, 貞治が初めて著した (独語による) 本格的な論文である. |
|||
 東京帝国大学紀要 理研 XIX (1903) |
 貞治の学位論文 (1901) |
||
| 序文を見ると, まず,「肯定的な解決が待たれる」クロネッカーの命題「虚二次体の相対アーベル数体は, 特異モデュラスをもつ楕円関数の変換方程式から生ずる体で尽くされる」が紹介される. その直後に次のような記載が現れる. |
|||
| … es gibt specielle Fälle dieser grossen Aufgabe, wo man von vorn herein eines ojücklichen Abschlusses sicher sein kann, nämlich die, wo die zu Grunde gelegten quadratischen Körper einclassig: sind, also z.B. durch die dritten und die vierten imajrinären Einheitswurzeln erzeugt werden … | |||
| 「この偉大なる表明には, 固より解決が保証される特別なケースが存在する」即ち「\(\mathbb{Q}\,\)に\(\,\zeta_{{}_{3}}\!=\!e^{2\pi i/3}\,\)または\(\,\zeta_{{}_{4}}\!=\!e^{2\pi i/4}\,\)を添加することで生成される (虚二次体の) 場合である」と記されるのである. 但し, この論文で用いられる手法は, (当然ながら) 類体論ではなく, \(\mathbb{Q}\,(\sqrt{-1\!\:}\!\:)\,\)上の不分岐拡大の非存在性およびヒルベルトの分岐理論を用いるものになっている. この論文の主要部は, §9以降であり, |
|||
| Wir kommen nun an den Zielpunkt dieser Abhandlung; es handelt sich darum, nachzuweisen, dass jeder im Bereich, der rationalen complexen Zahlen Abel'sche Körper ein LemnisJcatenhörper ist. | |||
| 即ち「論文の目的は, \(\mathbb{Q}\,\)上のアーベル体は悉くレムニスケート体なること」 なる記述で始まる. 「レムニスケート体なること」とは,「ヤコビの楕円関数の等分点を\(\,\mathbb{Q}\,(\sqrt{-1\!\:}\!\:)\,\)に添加して得られる」ことを意味する. 後年, その直後に現れる補助定理に (修正可能ではあるが) 誤りがあることが |
|||
| [近藤] 近藤武『Gauss 数体の Abel 拡大について』/『数学』第15巻第2号 (1963年10月), 岩波書店, p.110 | |||
| において指摘された. 貞治自身, この論文を「幼いもの」と謙遜しているが,「クロネッカーの青春の夢」の一部即ち虚二次体を\(\,\mathbb{Q}\,(\sqrt{-1\!\:}\!\:)\,\)とする場合に関してこれを肯定的に解決したことは, 当時の学位論文としては驚異的なレヴェルのものであった. 論文の最後に「1901年春, ゲッティンゲンにて」とあることから, ヒルベルトに「レムニスケート函数の虚数乗法をやらうと思ふ」と伝えた時点で, これが肯定的に解決し得る命題であることを貞治は既に看破していたのではないかと思われる. この時点で貞治が一般相対アーベル体の理論まで予想していたかと言えば, それは流石に穿ち過ぎというものであろう. なお, 貞治の言う「これを以て學位を頂戴した」について, 当時の |
|||
| 『官報』第6148號 (1903年12月28日付) | |||
| には次のような記載がある. |
|||
 |
|||
| 學位記 岐阜縣平民 從六位 高木貞治 右論文ヲ提出シテ學位を請求シ東京帝國大學敎授會ニ於テ其大學院ニ入リ定規ノ試驗ヲ經タル者ト同等以上ノ學力アリト認メタリ仍テ明治三十一年勅令第三百四十四號學位令第ニ條ニ依リ茲ニ理學博士ノ學位を授ク |
|||
| 論文審査ノ要旨 有理複素數ノ區域内ニ於ケルアーベル「キョルペル」ニ就テ | |||
| 此論文ハ東京帝國大學理科紀要第十九册第五編に掲載セラレタルモノニシテ緒論ノ外ニ第一章ヨリ第十四章ニ至ル十五章ヨリナルモノナリ | |||
| 以下, 40行以上に亘って論文の内容が詳細に説明されている.「官報」であるから一般人も目を通したはずであるが, ここに開陳されているものは専門用語を駆使した本格的な解説であって, 一般読者に対する配慮は一切見られない. 但し,「キョルペル」や「クラッセンツァール」など, (Körper や Klassenzahl のような原語表記がない状態での) カタカナ表記が目立ち, 内容を理解している者にとっても読みづらいものである (読み方も言語統一がされておらず,「ウァヰヤルストラスノ「ピー」函数」なる表記も見られる). 況してや専門外の者達には全く意味不明の解説であったことであろう. しかし, 説明内容に誤魔化しは一切なく, 正鵠を射た解説である. この解説は次のような表現をもって結ばれる. |
|||
 |
|||
| ……本論文ノ最終ノ目的タル有理複素數ヲ有理區域トナストキハ此區域内ニ於ケルアーベル「キョルペル」ハ「レムニスカーテン, キョルペル」ニ網羅セラルト云フ定理ヲ完全に證明セリ 著者ハ尚ホ本論文ノ目的タル定理ヲ證明セルノ傍硏究ノ餘波或ハ旣知ノ證明ヲ一層簡單ニシ或ハ旣知ノ定理ヲ擴張セリ 以上論文審査ノ結果トシテ本論文ノ提出者タル理學士高木貞治ハ理學博士ノ學位ヲ授與セラルヘキ資格ヲ有スルモノト認定ス |
|||
| 解説文の執筆者名の記載はないが, 内容の専門性から判断して (貞治自身ではないとすれば) 藤澤利喜太郎であろう. 彼のほかに, 貞治の学位論文を理解し得る者 (評価し得る者) は存在しなかったからである. 因みに, 貞治の学位記の前後には, 同時期に学位を授与された者として, 丹羽藤吉郎 (1856-1930, 薬学), 柴田承桂 (1850-1910, 薬学), 松村松年 (1872-1960, 昆虫学), 塚本靖 (1869-1937, 工学) の名が見られるが, 論文内容の詳細な解説が付されているのは貞治と松村のみである. |
|||
| |
|||
| §3.類体論を創設した頃 | |||
| §3-1. ヒルベルトの類体 | |||
| 前節において, [Weber2] 後半部, §179 (p.648) に現れたクロネッカーの命題「\(\mathbb{Q}\,\)上の任意の有限アーベル拡大は円分体である」が「後年の貞治を第一級の数学者へと押し上げる契機となった重要な定理であった」と記した. 但し, この時点で貞治がその重要性を認識していたか否かは判らない. しかし, 後に貞治は『代数的整数論』において, |
|||
| これは Kronecker (1875) が言明し, Heinrich Weber (1886) が証明した有名な定理であるが, 其の後 Hilbert (1896) が (中略) 簡単なる証明を与えた. (中略) 現今では, この定理は類体論の最も簡単なる一例に過ぎない (後略) | |||
| と記すことになる (p.110) のである. なお, "Walfram MathWorld" によれば, ヴェーバーによる "証明" は "incomplete" (不完全) であり,
最初に完全な証明を与えたのはヒルベルトであるという. なお,「類体」なる用語は, 貞治の発案ではない.『代数的整数論』p.170 の脚注には, |
|||
| 類体という語は, これよりも狭い意味で, Hilbertが用いた. 尤もこの語は既に楕円函数の虚数乗法論で用いられていた (H.Weber, Algebra, III). | |||
| とある. ヒルベルトが「類体」"Klassenkörper" なる用語を掲げたのは, 前掲の [Hilbert 報文] においてであった. 貞治が脚注に挙げたヴェーバーの [Weber3] を見ると, その第23節 §164.には, たしかに "Klassenkörper" の解説がある. しかし, これは [Hilbert 報文] が発表された翌年 (1898年) に出版されたものである. 先述したように, [Weber3] は『楕円関数と代数的数』([Weber4]) の改訂増補版であるから, まず, その原版である [Weber4] を見てみよう. すると, §110. p.439 および §117. p.482 において (綴りの異なる) "Classenkörper" なる用語が見つかった (この年代の書物は索引が付されていないため, 文脈から判断してこの用語の存在を探すほかはない. それゆえ, 他の箇所にも存在する可能性がある). そこには, 次のような記載がある (p.439). |
|||
| Wir betrachten jetzt den algebraischen Zahlkörper, welcher die gemeinschaftliche
Norm aller zu einer bestimmten Determinante \(-m\) gehörigen Körper
der Classeninvarianten erster oder zweiter Art ist, unt der, wie wir im
vorigen Paragraphen gesehen haben, aus den rationalen Functionen einer
Classeninvariante und \(\sqrt{-\!\:m\,}\) besteht. Er kann daherm wenn \((k),(k^\prime),(k^{\prime\prime}),\,\cdots\) dir sämmtlichen Classeninvarianten sind, nach §58, durch \(\frak{K}\,\)\((k,k^\prime,k^{\prime\prime},\cdots)\) oder durch \(\frak{K}\)\(\,(k,\sqrt{-\!\:m\,}\!\:)\) bezeichnet werden. Wir wollen ihn den Classenkörper der Determinante \(-\!\:m\,\) nennen und kurz mit \(\frak{K}\) bezeichnen, während der quadratische Körper \(\frak{K}\)\(\,(\sqrt{-\!\:m\,}\!\:)\) mit \(\varOmega\) bezeichnet sei. |
|||
| ここで扱われるのは, 虚二次体\(\,k\,\)における類不変量および\(\,\sqrt{-\!\:m\,}\,\)の有理関数から構成した「類体」である. 楕円関数の虚数乗法論を用いて,そのガロア群が絶対イデアル類群と同型かつ不分岐であり, 単項化定理を満たすことに言及している. 一方, [Hilbert 報文] pp.175-546 における第15章 §58. の最後には, |
|||
| Satz 94. Wenn der relativ-cyklische Körper K von ungeradem Primzahl-Relativgrade\(\:l\:\)die Relativdifferente\(\:1\:\)in Bezug auf\(\:k\:\)besitzt, so giebt es stets in\(\:k\:\)ein Ideal\(\:\large{\mathfrak{i}}\), welches nicht Hauptideal in\(\:k\:\)ist, wohl aber ein Hauptideal in\(\:K\:\)wird. Die \(l\,\)te Potenz dieses Ideals\(\:\large{\mathfrak{i}}\:\)ist dann notwendig auch in\(\:k\:\)ein Hauptideal, und die Klassenanzahl des Körpers\(\:k\:\)ust mithin durch\(\:l\:\)teilbar. | |||
| 「定理94. 有限次代数体\(\,k\,\)に対し, 奇素数次数\(\,l\,\)の不分岐巡回拡大\(\,K\!\!\:/k\,\)が存在するならば, \(k\,\)においては単項イデアルではないが\(\!\:K\!\:\)においては単項イデアルとなる\(\,\large{\mathfrak{i}}\,\)(当然ながら\(\,{\large{\mathfrak{i}}}^{\!\:l}\,\)は\(\,k\,\)の単項イデアル) が存在し, \(k\,\)の類数は\(\,l\,\)で割り切れる.」 | |||
| が掲げられ, その証明に続けて, | |||
| Wegen der engen Beziehung, die nach Satz 94 der Körper\(\:K\:\)zu gewissen Idealklassen des Körpers\(\:k\:\)aufweist, werde\(\:K\:\)ein Klassenkörper des Körpers\(\:k\:\)genannt. | |||
| 「この定理における\(\!\:K\!\:\)と\(\,k\,\)の特定のイデアル類群との密接な関係をもって, \(K\,\)を\(\,k\:\)の類体と称する.」 | |||
| と記される. 換言すれば, ヒルベルトは「\(K\!\!\:/k\,\)が不分岐の場合, 即ち\(\,k\,\)の一次素イデアルが単項イデアルである場合に限り\(\!\:K\!\:\)の一次素イデアルの積に分解されるとき, \(K\!\:\)を\(\,k\,\)上の類体である」としたのである (『代数的整数論』p.180). これが, 貞治の言う「狭い意味での類体」で, いわゆる「ヒルベルト類体」もしくは「絶対類体」に該当する. では次に, [Weber4] の改訂増補版である [Weber3] を見てみよう. その第23節では, 綴りを改めた "Klassenkörper" 論が展開される. 前半部では, ヤコビおよびヴァイエルシュトラスによる楕円関数の虚数乗法が論じられ, 一次素イデアル, ディリクレ級数などが解説される. 前後を含めた引用は長文になるため割愛するが, 節の後半において, 次のような定義が現れる (p.607). |
|||
| Definition des Klassenkörpers. Die Primideale \(\mathfrak{p}_{{}_{1}}\) ersten Grades der Hauptklasse \(\overline{A}_1\), und nur diese, sollen im Körper \(\mathfrak{K}(A)\) wieder in Primideale ersten Grades zerfallen. |
|||
| 「類体の定義. 首類 (単位類)\(\,\overline{A}_1\,\)に属する一次素イデアル\(\,\mathfrak{p}_{{}_{1}}\,\)のみが体\(\,\mathfrak{K}(A)\,\)の一次素イデアルに再び分解される.」 | |||
| この引用箇所のみでは正確な表現ではないが, 前後の文脈と併せて判断すれば, イデアルの合同類別に着目し, 単項化定理から離れて一次素イデアルの完全分解性をもって類体を把捉するもので, これは現行の定義に沿うものと言ってよい. ヴェーバーは, ヒルベルトのイデアル類群の概念を拡張し,「次数\(\,n\,\)のガロア拡大\(\,K\!\!\:/k\,\)が類数\(\,h\,\)の合同イデアル群\(\,H\,\)に対応し, \(h\!=\!n\,\)である (すなわち\(\,H\!\:\)に属する絶対次数1の素イデアル\(\,\mathfrak{p}\,\)が\(\,k\,\)の単項イデアルで, \(\mathfrak{p}\,\)が全て\(\!\:K\!\:\)の一次素イデアルに分解される) とき, \(\,K\,\)を\(\!\:H\!\:\)に対応する類体と称する」としたのである (『代数的整数論』p.170). |
|||
| §3-2. 東京帝国大学教授就任 | |||
| 1901年, ドイツ留学から帰国した貞治は, 留学中に助教授の辞令を受けていた. 1903年に (先述した) 学位論文 [高木6] が認められると, 翌1904年, 29歳で東京帝国大学理科大学 (現在の東大理学部) の教授に就任した. 引き続き,『回顧と展望』を見てみよう. |
|||
| 1901年に歸つて來てからは, いろいろな講義をさせられた. 代數曲線とか, その他何をやつたか忘れてしまつたが, (中略) その裡に, 吉江君や,
中川君が歸つて來られて, 私もさういふ餘計な仕事はやらなくて濟むやうになつた. 全體私は殊にさういふ人間であるが, 何か刺戟がないと何もできない性質である. 今と違つて, 日本では, つまり「同業者」が少いので自然刺戟が無い. ぼんやり暮してゐてもいいやうな時代であつた. |
|||
| [百年史上] (p.172) によれば, 1901年~1904年当時, 数学科の講座を受け持っていたのは, |
|||
| ・第一講座 [幾何学] 藤澤利喜太郎 (1898.7-1903.9), 坂井英太郎 (1903.9- ) ・第二講座 [関数論] 藤澤利喜太郎 (1893.9- ) ・第三講座 [代数学] 高木貞治 (1901.12- ) ・第四講座 [微分方程式論] 吉江琢兒 (1902.9- ) ・応用数学講座 長岡半太郎 (1896.9-1901.9) |
|||
| であった (括弧内の年号は担当期間を表す). 初代教授の菊池大麓は, 1898年より総長に就任しており, 講座担当から外れていた. また, 応用数学講座は,
1901年9月以降, 理論物理学講座と改称され物理学科の所属となったという. 上記引用文中の「中川君」は, 中川銓吉 (1876-1942) を指す. 中川は, 1898年に東京帝大を卒業し, 第二高等学校 (1898-1899) で教鞭を執った後にベルリン留学 (1901-1905) を経て, 帰国後の1907年5月から第一講座を担当したという ([百年史上] pp.155, 171-172, 183). 帰国後の貞治は, 教授として学生の指導に携わる中で, 数学者としての業務以外の仕事も任されたのであったのであろうか.「餘計な仕事」が何を指すものかは不明であるが, 帰国後の貞治は, 類体論に関する論文を発表する1914年までの10年間, 学位論文ないし類体論に関連した論文を発表しなかった. この時期の事情について, 本多欣哉は「一見スランプとも考えられるわけであるが, これはやはり高木の個人的な正確に関係した現象であろう. (中略) 小さな研究論文ばかりを次々と発表して行くやり方は, あまり好まなかったようである.」と述べている.「この10年間の無風状態の間に, 数学の学力を深め充実して行ったのであって, それがのちに, 代数学と解析学を縦横に用いる, 類体論の深い複雑な研究の土台となっている」という ([科学技術史] pp.211-212). 貞治の論文集 |
|||
| [高木全集] "The Collected Papers of TEIJI TAKAGI" 岩波書店, 1973. | |||
| に収録されている計26編 (英文14編, 独文10編, 仏語2編) の論文中, 最初の6編は1903年以前に発表されたものである. |
|||
 高木貞治論文全集 (岩波書店, 1973) |
 第2版 (シュプリンガー東京, 1990) |
||
| 以下, [高木全集] に収録されている論文を順に見てみよう. 1903年以前に発表された論文のうち, 5編 (英文) は,『東京數學物理學會報告』に掲載された |
|||
| [高木1] "On Weierstrass' proof of the fundamental theorem of algebra" (ヴァイエルシュトラスによる代数学の基本定理の証明) Proc. Phys.-Math. Soc. Japan, Ser.II, Vol.1, 1902, pp.56-58. | |||
| [高木2] "On the 'zweigliedriger Modul" (二次のモデュールについて) Proc. Phys.-Math. Soc. Japan, Ser.II , Vol.1, 1902, pp.102-103. | |||
| [高木3] "A simple example of the continuous function without derivative" (導関数が存在しない連続関数の簡単な例) Proc. Phys.-Math. Soc. Japan, Ser.II, Vol.1, 1903, pp.176-177. | |||
| [高木4] "Mathematical notes" (数学ノート) Proc. Phys.-Math. Soc. Japan, Ser.II , Vol.2, 1903, pp.25-29. | |||
| [高木5] "A simple proof of the law of reciprocity for quadratic residues" (平方剰余の相互法則の簡単な証明) Proc. Phys.-Math. Soc. Japan, Ser.II, Vol.2, 1903, pp.74-78. | |||
| であり, この論文集において僅か2,3ページ程度の (本多の言う)「小さな研究論文」である. とは言え, 何れも貞治の独自の視点に基くオリジナル性に富んだ研究であり, 味わい深い内容をもっている. 例えば, [高木1] では, 単なるヴェイルシュトラスの手法の紹介に留まらず, より洗練された形へと改良が施された証明が紹介されており, [高木3] においても貞治独自の優れたセンスが際だつもので, 後に「高木曲線」として知られるフラクタルの実例がここに見出される (この曲線は, 後年の『解析概論』でも解説される). また, [高木5] では, ガウスによる第三証明が幾何学的手法をもって簡明な形に改良された証明が開陳されているのである. これらより前に書かれた論文が, 貞治の学位論文, 即ち前出の [高木6] であった. これらの論文を著した後, 10年もの間, 貞治は論文を全く発表しなかった. とは言え, 貞治が「ぼんやり暮してゐて (中略) 何もしないでゐた」はずはない. 学位論文を発表した時点で, 数学研究における貞治の目標は既に確定していたことであろう.「クロネッカーの青春の夢」の解決, さらにはヒルベルトのパリ講演における「類体の構成問題」の解決である. 1914年から1917年にかけて, 学位論文に続く5編の論文 (英文1編, 独文4編) が『東京數學物理學會記事』に立て続けに発表されることになる. |
|||
| [高木7] "On a fundamental property of the "equation of division" in the theory of complex multiplication" (虚数乗法論における等分方程式の或る基本性質) Proc. Phys.-Math. Soc. Japan, Ser.II, Vol.7, 1914, pp.414-417. | |||
| [高木8] "Zur Theorie der relativ-Abel'schen Zahlkörper I" (相対アーベル数体論について 第一) Proc. Phys.-Math. Soc. Japan, Ser.II, Vol.8, 1915, pp.154-162. | |||
| [高木9] "Zur Theorie der relativ-Abel'schen Zahlkörper II" (相対アーベル数体論について 第二) Proc. Phys.-Math. Soc. Japan, Ser.II, Vol.8, 1915, pp.243-254. | |||
| [高木10] "Zur Theorie der komplexen Multiplikation der elliptischen Funktionen" (楕円関数の虚数乗法論について) Proc. Phys.-Math. Soc. Japan, Ser.II, Vol.8, 1915, pp.386-393. | |||
| [高木11] "Über eine Eigenschaft des Potenzcharacters" (冪剰余記号の或る特性について) Proc. Phys.-Math. Soc. Japan, Ser.II, Vol.9, 1917, pp.166-169. | |||
| さらに, 1919年には,『日本數學物理學會記事』に |
|||
| [高木12] "On norm-residues" (ノルム剰余について) Proc. Phys.-Math. Soc. Japan, Ser III, Vol.2, 1919, pp.43-45. | |||
| が発表された. 標題から察し得るように, これら一連の論文は各々が類体論の一部を成すものである. 貞治は, ヴェーバーによるイデアル類群の拡張を採り入れ, ヒルベルトの絶対類体における不分岐性を取り除く方針で類体論創設の土台を構築していったのであった. この方針のもとで, [高木8] において類体の存在を示すに至ったのである. 但し, この論文では簡潔に論拠が示されるのみであった. |
|||
| §3-3.『相対アーベル体の理論』 | |||
| 完全な証明が施されたのは, その翌年に『東京帝國大學理學部紀要 XLI』に発表された『相対アーベル体の理論』 |
|||
| [高木13] "Ueber eine Theorie des relativ Abel'schen Zahlkörpers" J. Coll. Sci. Imp. Univ. Tokyo, Vol.41, Art.9, 1920, pp.1-133. | |||
| においてである (1920年7月31日出版). この研究過程に関して,『回顧と展望』では次のように回想されている. |
|||
| 1914年に世界戰爭が始まつた. それが私にはよい刺戟であつた. 刺戟といふか, (中略) ネガティヴの刺戟だが, つまりヨーロッパから本が來なくなつた.
(中略) 學問をしようといふなら, 自分で何かやるより仕方が無いのだ. (中略) 「類體論」の話を少しすると, あれはヒルベルトに騙されてゐたのです. 騙されたといふのは惡いけれども, つまりこつちが勝手に騙されてゐたのです. ミスリードされたのです. (中略) ヒルベルトは, 類體は, 不分岐だといふのであるが, (中略) そんな風に私は思はされた. 所が, 本が來なくなつて, 自分でやり出した時に, さういふ不分岐などといふ條件を捨ててしまつて, 少しやつてみると, (中略) 要するにアーベル體は類體なりといふことにぶつかつた. 當時これは, あまりにも意外なことなので, それは當然間違つてゐると思うた. (中略) 何が間違ひか, 實例を探して見ても, 間違ひの實例が無い. |
|||
| ヒルベルトによる絶対類体\(\,K\!\!\:/k\,\)は, 代数関数論との関連性から現れ, リーマン面の分岐理論に基く不分岐拡大に着想を得たものであった. |
|||
| 貞治は, [高木13] の序文において, [Hilbert 報文] および | |||
| [Hilbert1] "Über die Theorie der relativ-Abel'schen Zahlkörper" Nachr. Gesell. Wiss. Göttingen, 1898 [Hilbert2] "Über die Theorie der relativquadratishen Zahlkörper" Math. Ann. Vol.51, 1899. |
|||
| を, フルトヴェングラー (Philipp Furtwängler, 1869-1940) やフェター (Rudolf Fueter, 1880-1950) などの論文 | |||
| [Furtwängler1] "Allgemeiner Existenzbeweis für den Classenkörper eines beliebigen algebraischen Zahlkõrpers" Math. Ann. 63, 1907. | |||
| [Fueter] "Abel'sche Gleichungen in quadratisch-imaginären Zahlkörpern" Math Ann. Vol.75, 1914. | |||
| と共に, 重要かつ影響を受けた参考文献として挙げている. [Hilber1] および [Hilbert2] において, ヒルベルトは,「\(K\!\!\:/k\,\)はヒルベルト類体 (最大不分岐アーベル拡大) で, そのガロア群は\(\,k\,\)の狭義イデアル類群と同型であること, \(k\,\)の素イデアル\(\,\mathfrak{p}\,\)の\(\,K\!\!\:/k\,\)における分解の様相は\(\,\mathfrak{p}\,\)の属する狭義イデアル類により定まり, \(\mathfrak{p}\,\)が総正な単項イデアルである場合のみ\(\,\mathfrak{p}\,\)は\(\,K\!\!\:/k\,\)で完全分解すること, \(k\,\)のイデアルは全て\(\,K\,\)の単項イデアルとなること」を類体の諸性質として記していたのであった. フルトヴェングラーは, [Furtwängler1] において, 一般の有限次代数体に対するヒルベルト類体の存在を示した. ただし, ヒルベルトの言う「類体の諸性質」(上記において, \(K\,\)が最大不分岐アーベル拡大体なることや, 最後に掲げた「単項化定理」など) は, この時点では解決できていなかった. 一方, フェターは [Fueter] において, 虚二次体\(\,K\,\)の奇数次アーベル拡大体は\(\,K\,\)に特異モデュラス \(j\!\:(\tau_{\!\!\:{}_{K}})\,\)と\(\,\zeta_n\!=\!e^{2\pi i/n}\,\)を添加した拡大体に含まれることを示していた. これは「クロネッカーの青春の夢」に繋がるものであり, 貞治の研究意欲に刺戟を与えたであろうと思われる. 貞治は, 最初はヒルベルトと同様に不分岐性を前提条件として考究を進めたが,「クロネッカーの青春の夢」を念頭に置く中で, ヴェーバーのように分岐性を視野に入れて考えるようになった. [高木13] では, 分岐をもつアーベル体を追究していった結果,「アアベル体即ち類体という帰結」(『代数的整数論』序) を得たのである. 貞治は, そのような事情をもってヒルベルトに「ミスリードされた」と述べたのである. [高木13] は, [高木全集] 全266頁のうち約3分の1 (72~167頁) を占める長大な論文であり, 序文と5つの章から構成される (以下に用いられる記号は, 論文におけるそれとは異なるものを採用している). 第1章「一般類体論」"Der allgemeine Classenkörper" では, 合同類群や導手に関して言及され, Satz6に基いて類体の一意性が示される. ここでは, \(l\,\)を奇素数として\(l\,\)次巡回拡大\(\,K/k\,\)の分岐イデアルに必要な導手\(\,\mathfrak{f}\,\)が設定され, \(K\,\)に対応する合同イデアル群\(\,\mathfrak{H}\,\)が\(\,K/k\,\)のイデアルのノルムにより規定されている. 第2章「素数次相対巡回体の種の理論」"Die Geschlechter im relativ cyclischen Körper vom Primzahlgrade" では, ノルム剰余やアンビグ (特異) 類および類の種 (Geschlecht) に言及され, 類体の基本定理が (証明は後述するとして) 提示される (Satz 13). 第3章「一般類体の存在証明」"Existenzbeweis für den allgemeinen Classenkörper" では, 奇素数次の場合, 素数冪次の場合, 一般の場合に分けて, 類体の存在定理が証明される (Satz 23). 第4章「他の諸定理」"Weitere allgemeine Sätze" では,「相対アーベル体は類体」なることが提示され (Satz 28), それまでの諸結果と併せて同型定理 (Satz 29) および分解定理 (Satz 30) が示される. 第5章「楕円関数の虚数乗法論への応用」"Anwendung auf die Theorie der complexen Multiplication der elliptischen Functionen" では, 類体論の諸結果が「クロネッカーの青春の夢」に適用され (Satz 37), 論文は締め括られるのである. |
|||
| 以下, | |||
| [彌永数論] 彌永昌吉『数論』岩波書店, 1969, pp.448-487. [河田数論] 河田敬義『数論』岩波書店, 1992, pp.393-429. [谷山全集] 谷山豊『[増補版] 谷山豊全集』日本評論社, pp.183-198, pp.212-220, pp.337-345. [百年史下]『日本の数学100年史 下』岩波書店, 1984, pp.64-73, pp.241-248. |
|||
| などを援用して, 貞治がこれら論文を発表した頃とその後の状況について概観しよう. 代数体\(\,k\,\)の拡大体を\(\,K\,\)とし, 整イデアル\(\,\mathfrak{m}\,\)(有限素点および無限素点の形式的有限冪積) と互いに素なる\(\,k\,\)の分数イデアルの成す乗法群\(\,\mathfrak{A}_{\mathfrak{m}}\,\)と, 射類\(\,\mathfrak{S}_{\mathfrak{m}}\,\)(\(=\!\{(\alpha)\,;\,\alpha\!\equiv\!1\, \mathrm{mod}.\!\!\:\mathfrak{m}\}\,\)(\(\alpha\,\)は総正)) により得られる射類群\(\,\mathfrak{A}_{\mathfrak{m}}/\mathfrak{S}_{\mathfrak{m}}\,\)の部分群\(\,\mathfrak{H}_{\mathfrak{m}}/\mathfrak{S}_{\mathfrak{m}}\,\)を考える. \(K\!\!\:/k\,\)がガロア拡大であり, \(\mathfrak{m}\,\)と素なる一次素イデアル\(\,\mathfrak{p}\,\)が\(\,\mathfrak{p}\!\in\!\mathfrak{H}_{\mathfrak{m}}\,\)なる場合に限り\(\,K\,\)の一次素イデアルの積に完全分解されるとき, \(\,K\,\)を\(\,\mathfrak{H}_{\mathfrak{m}}\,\)の類体として定義する. ヒルベルトが定義した意味での類体は, \(\mathfrak{m}\!=\!(1)\,\)(\(\mathfrak{H}_{\mathfrak{m}}\,\)が単項イデアル群) となる場合にほかならない. |
|||
 彌永昌吉『数論』(岩波書店, 1969) |
 河田敬義『数論』(岩波書店, 1992) |
||
| 貞治は, この意味での類体に関して, 次の諸定理を示したのである. |
|||
| i) 類体の一意性 \(k\,\)におけるイデアル群\(\,\mathfrak{H}_{\mathfrak{m}}\,\)上の類体\(\,K\,\)は (存在するならば)
一意的である. ii) 存在定理 \(k\,\)における任意のイデアル群\(\,\mathfrak{H}_{\mathfrak{m}}\,\)に対応する類体\(\,K\,\)が存在する. iii) 分岐定理 類体\(\,K\!\!\:/k\,\)の導手は\(\,K\!\!\:/k\,\)において分岐する\(\,k\,\)の全ての素イデアルを含む. iv) 同型定理 類体\(\,K\!\!\:/k\,\)のガロア群は\(\,k\,\)における類群\(\,\mathfrak{A}_{\mathfrak{m}}/\mathfrak{H}_{\mathfrak{m}}\,\)と同型である. v) 分解定理 素イデアル\(\,\mathfrak{p}\!\in\!\mathfrak{H}_{\mathfrak{m}}\,\)は, \(\mathfrak{p}^f\!\in\!\mathfrak{H}_{\mathfrak{m}}\,\)となる最小の\(\,f\,\)に対して, 類体\(\,K\!\!\:/k\,\)において\(\,f\,\)次の素イデアルに分解される. |
|||
| 中でも最も重要な定理は, 彌永が「高木理論の驚嘆すべき結果」([彌永数論] p.466) と称する |
|||
| Satz 28. Alle relativ Abel'schen Körper in Bezng auf einen beliebigen algebraischehen Körper werden durch die Classenkörper nach den Idealmoduln in demselben erschöpft. | |||
| vi) 基本定理 代数体\(\,k\,\)の全てのアーベル拡大は\(\,K\,\)は, \(k\,\)の或るイデアル群\(\,\mathfrak{H}_{\mathfrak{m}}\,\)に対する類体である. | |||
| であった. これは, 当時の貞治自身でさえ「当然間違つてゐると思」ったほど「あまりにも意外なこと」であったのである. 余談であるが, [高木13] の序文に重要かつ影響を受けた参考文献として挙げられた [Furtwängler1] や [Fueter] に関して, 貞治は『回顧と展望』[速記版] に後日談を打ち明けている. |
|||
| いろいろ人のやつたものを讀んでフルトヴェングラー, フユーターを讀んだといふけれども, 實はさう詳しくは讀まなかつた. フユーターで想ひ出しましたが, その頃フユーターが出したものを諸君御存知ないかも知れませぬけれとも, 數學のあゝいふ雜誌に無粹だらうと思ふのです. クロネツカーの問題が解けたといふ意味で, 大きな何號活字といふのですか, 表題に使ふやうな活字でそのことを印刷したものです. クロネツカーのあれが實現されたといふやうなことを今でも記憶してゐるのですけれども, 御覽になつた方があるかも知れませぬが, 讀んで見るとやはりよく判らないし面白くなかつた. |
|||
| ここにも数学に対する貞治の真摯な姿勢が垣間見える. 数学者は数学的な真理を見極めることに主眼をおくべきであり, その研究成果を (スポーツ競技で勝利したかのように) 大袈裟に飾り立て騒ぎ立てて宣伝するようなことは数学者としてあるいは数学誌においては相応しくない, と述べたのである. また,「よく判らないし面白くなかつた」なる表現も, 分からないものについては分かったフリをしないという, 貞治の姿勢が窺える. 数学的な内容として面白いか面白くないかについても, 後年, 貞治が学生達を指導する際の一つの基準として用いたようである (これに関しては最終節 (§6.) で触れることにする). |
|||
| |
|||
| §3-4. ストラスブール万国数学者会議 | |||
| [高木13] を完成した貞治は, 直ちに, 仏語による報告書 |
|||
| [高木14] "Sur quelques théorèmes généraux de la théorie des nombres algébriques" (代数的整数論におけるいくつかの一般的な定理について) C.R. Congrès Internat. Math. Strassbourg, 1920, pp.185-188. | |||
| を書き上げた. これは, 1920年にストラスブールで開催された万国数学者会議に間に合わせるために書かれた研究報告である. 貞治はここで, 自身の「類体論」に関する結果を初めて国際的な学会で発表したのであった. この会議の模様について, |
|||
| [本田5] 本田欣也『高木貞治の生涯』/ 日本評論社『数学セミナー』1975年5月号, pp.40-41. | |||
| には (小倉金之助の談話をもとに) 次のように書かれている. | |||
| 高木は日本代表として挨拶をのべたが, その中で, 敗戦国ドイツの数学者がこの会議からしめ出されていることに, 遺憾の意を表明した. (中略) コングレスでは, 毎日9時から12時まで, 講演が行なわれ (中略) ひとり20分の割り当てであった. 高木は, 第4日の (中略) 10時ごろから, その講演を行なった. 標題は「代数体の理論のいくつかの一般的定理について」で (中略) 黒板には何も書かず, フランス語の原稿をただよみつづけた. |
|||
| 貞治自身は, 帰国後の講演記録 |
|||
| 『すとらすぶるぐニ於ケル數學者大會ノ話』/『日本中等敎育數學會雜誌』3巻4-5号, 1921, pp.113-116. | |||
| において, | |||
| 今度ノ數學者大會ハ昨年9月22日カラ9月30日マデノ間佛國ノ新領土あるさすノすとらすぶるぐデ開カレタノデス. (中略) 講演ハ四部に分レ 第一部 整數論代數學及ビ函數論 第ニ部 幾何學 第三部 應用數學 第四部 數學歴史, 敎授法等 少ナイ部ハ十二三名カラ多イノハ三十四五位名アリマシタ. (中略) 四部を同時ニ聽クコトハ出來ヌノデ銘々勝手ニ好キナノヲ聞クコトニナリマス (後略) |
|||
| と述べ (pp.113-114), 独墺など反連合国側 (中央同名国側) の国々が学会から排除されていたことへの批判にかなりの紙面を割いた後, (読者が詳しく知りたいと思っていたであろう) 肝心の貞治自身の発表については, 末尾にひとこと | |||
| 本邦人ノ參會者ハ大阪ノ小倉博士ト小生トノ二人デ小倉君ハいんたーぽれーしよんノ理論ニツキテ講演セラレ, 小生ハ整數論ニ關スル硏究ノ結果ヲ披露致シマシタ. | |||
| とだけ記して (p.116) 学会報告を終えてしまっている. 上掲の [高木14] の内容は先述した諸定理の結果を纏めたものであり, そのまま話せば恐らく15分程度の時間は直ちに経過してしまったことであろう. 貞治自身の『回顧と展望』によれば, |
|||
| 戰爭の直後, 聯合國とドイツ側と分離した時代で, (中略) 整數論の話などを持出すには最も不適當な所であつた. 類體論などに理解を持つた人は僕の知つてゐる所では二三人位で, 先づフューター, あれはスウィス人だから來てゐた. それから佛蘭西ではシャトレといふ人, その外ではアダマール, 彼は問題を理解する. 興味を有つか, 有たんかは知らんが, 問題を理解する人である. まあ當てになるのは, こんな連中だけであつた. なんでもあの時, レセプションの晩に, 私の近くで,「あの日本人が整數論の話をするといふではないか. 多分フェルマーをやるんだらう. こいつは面白いぞ」などと私語するのが聞えて, 私は苦笑した. 會議では15分位の講演をしたけれども, 無論, 反響も何もありはしない. |
|||
| という状況であった. 嘗てのドイツと同様, ここでも日本人による数学研究が西欧では如何に軽んじられていたかが窺える. 彼らから見れば, 身のほど知らずの日本人が国際会議に押しかけて来て, 数学愛好家にありがちな「フェルマーの最終定理」の一部をかじって愚にもつかない成果を発表しようとしているとでも思ったのであろう. 小倉金之助も,「その会議に出席した日本人は, 高木先生と私の二人でした」と述べ, 貞治の講演に関しては「何しろごく短い時間で, (中略) 先生の講演には誰の質問も議論もありませんでした.」と記している (前掲書『小倉] p.351). 類体論に最も深い興味関心を示したはずのドイツ人数学者達にこの講演を聞かせることが適わなかったことは, 貞治にとって大きな不運であった. 理解される可能性が低いどころか無名の東洋人を嘲笑するような雰囲気の中で「無論, 反響も何もありはしない」ことを予想し,「黒板には何も書かず, フランス語の原稿をただよみつづけた」貞治の無念さは, 察するに余りある. このとき既に45歳になっていた貞治であったが, 国際的には全くの無名の存在であったのである. フェター (前出) は, [高木13] の序文に記載されている通り, [Fueter] を著した数学者であるから, 貞治の講演には少なからず関心を抱いたと思われるが, 彼も何の反応も示さなかったとすると, 講演内容を理解できなかったか, あるいはその意外な結論に対して半信半疑であったか, の何れかであろう (後年になってフェターが貞治の理論を高く評価するようになったことは, 現在ではよく知られている). 貞治は, この報告書の最後で, 今後取り組むべき「代数的整数論における重要な問題」として「非アーベルな正規拡大と基礎体のイデアル群とは一意的に対応するか否か」を掲げた. これはさらにレヴェルの高い問題であり, 類体論の重要性を含め, これがその後の数学者達によって重要な研究対象であることを認識されるまでには, しばらく時間を要することとなる. [本田] によれば, 貞治はこの講演の後, ドイツに立ち寄ったという.「旧師ヒルベルトやランダウに会ったが, この地の整数論の若手にジーゲルという俊秀がいることをきき及んだ」という. 帰国後, 貞治はジーゲル (Carl Ludwig Siegel, 1896-1981) 宛に [高木13] の別刷を送った. 貞治の立場からすれば当然であるが, ドイツの数学者達に真っ先に類体論の成果を伝えたかったのであり, 結果的には, ジーゲルに論文を送ったことが類体論を広める重要な契機となったのであった. |
|||
| その後, | |||
| [高木15] "Sur les corps résolubles algébriquement" (代数的に可解な体について) C.R. Acad. Sci. Paris, Vol.171, 1920, pp.1202-1205. | |||
| [高木16] "Note on the algebraic equations" (代数方程式に関するノート) Proc. Phys.-Math. Soc. Japan, Ser.III, Vol.3, 1921, pp.175-179. | |||
| の2篇の短い論文が書かれ, 各々, 科学アカデミー ('Académie des Sciences'),『日本數學物理學會誌』に発表された. 前者は, 三次剰余と原始二次形式の類数に関するデデキントの結果を素数次の拡大体の場合に一般化したもので, 仏国滞在時のものらしく仏文で執筆されている. 後者は, グレース (John Hilton Grace, 1873-1958) の無極性定理に基いて微分合成多項式の零点の位置を特定するもので, 英文で執筆された. [高木13] を類体論に関する第一論文とすれば,『東京帝國大學理學部紀要 XLIV』に発表された『任意の代数体における相互法則について』 |
|||
| [高木17] "Ueber das Reciprocitätsgesetz in einem beliebigen algebraischen Zahlkörper" J. Coll. Sci. Imp. Univ. Tokyo, Vol.44, Art.5, 1922, pp.1-50. | |||
| は, 類体論に関する第二論文となる. ここに掲げられた参考文献は, ヒルベルトのものに関しては [高木13] の場合と同様であるが, フルトヴェングラーのものに関しては, |
|||
| [Furtwängler2] "Über die Reziprozitätsgesetze zwischen \(l^{\!\:\mathrm{ten}}\) Potenzresten
in algebraischen Zahlkörpern, wenn \(l\) eine ungerade Primzahl bedeutet." Math. Ann. Vol.58, 1904. [Furtwängler3] "Die Reziprozitätsgesetze für Potenzreste mit Primzahlexponenten in algebraishen Zahlkörpern" Math. Ann. Vol.67, 1909, Vol.72, 1912, Vol.74, 1913. |
|||
| となっている. [高木17] は, ヒルベルトのパリ講演 (第2回国際数学者会議) における「任意の代数体における一般相互法則」(「ヒルベルトの23の問題」の中の「第9問題」) に関する論文である. この問題については, 既にフルトヴェングラーが |
|||
| [Furtwängler4] "Allgemeiner Existenzbeweis für den Klassenkörper eines beliebigen algebraischen Zahlkörpers" Math. Ann. Vol.63, 1904. | |||
| において奇素数次に関して証明し, 続いて [Furtwängler3] において全ての素数冪次に関して冪剰余の相互法則を示していた. 貞治は, 類体論を応用してフルトヴェングラーの方法よりも洗練された形で任意の素数冪に関する相互法則を示したのである. さらに, \(k\,\)を基礎体とするクンマー拡大\(\,K\!\!=\!\!\:k\!\:(\sqrt[l\!\:]{\mu\,})\,\)(\(\,l\,\)は奇素数, \(\mu\!\in\!k\,\)) に対応する\(\,k\,\)のイデアル群\(\,\mathfrak{H}(K\!\!\:/k)\,\)の導手を\(\,\mathfrak{f}\,\)とするとき, \(k\,\)のイデアル\(\,\mathfrak{a}\,\)に対応する\(\,l\:\)冪剰余記号\(\,\displaystyle{\left(\!\frac{\!\:\mu\!\:}{\mathfrak{a}}\!\right)}\,\)の値は, \(\mathrm{mod}.\mathfrak{f}\,\)で\(\,\mathfrak{a}\,\)が属する剰余類のみで定まることを明示し, 後にアルティン (Emil Artin, 1898-1962) により証明される「一般冪剰余の相互法則」を予見したのであった. [高木17] の末尾を見ると,「1920年6月に完成」とある. 類体論に関して述べた2篇の主論文 (第一, 第二) は, 発表年月には2年ほどの差異はあるものの, それまでの研究の成果を纏めて一気に書かれたものらしい. |
|||
| §3-5. 一般冪剰余の相互法則 | |||
| 発表当時は冷遇された「高木類体論」がその後, 如何にして世界に知られ, 高く評価されるようになったか. その経緯について, [本田5] に詳細なる記載がある. まず, その契機について引用してみよう. |
|||
| ある日のこと, ジーゲルとアルチンが代数体の話をしていたときに, ジーゲルは, 高木が送った論文をアルチンに示して, よんで見ないかとすすめた.
(中略) 晩年のアルチンに会った筆者に,「非常な讃歎の年をおぼえた. 難解ではなかった. むしろ, 一切が明晰であった」と語っている. アルチンは高木に, 自分にも別刷を1部送ってくれるよう, 依頼の手紙を出した. それはやがて届き, さらに第2論文の別刷も送られてきた. (中略) アルチンが, 相互法則の最も一般的な形を, フロベニウス置換により定式化するアイディアを得たのは, 1923年のことで, それは高木の第2論文から示唆されたのである. |
|||
| 貞治から論文を送られたジーゲルが, 新進気鋭の若手数学者, 24歳のアルティン (Emil Artin, 1898-1962) にその論文を薦めたことが, 後年, 広く類体論が知られるようになったことの発端であったようである. アルティンは, フロベニウスの非可換環に対する群指標の理論をもとにガロア群の指標に対する\(\,L\,\)関数を導入した. 類体論における同型定理と分解定理を, 基礎体の素イデアルとそのフロベニウス置換とを対応させることにより, |
|||
| [Artin] "Beweis des allgemeinen Reziprozitätsgesetzes" Abh. Math. Semin. Univ. Hambg. Vol.5, 1927, pp.353–363. | |||
| において,「一般相互法則の証明」を次のような形で示したのであった. \(k\,\)の有限アーベル拡大\(\,K\!\!\:/k\,\)で不分岐な\(\,k\,\)の素イデアル\(\,\mathfrak{p}\,\)(その絶対ノルムを\(\,N\mathfrak{p}\,\)とする) に対し, 任意の整イデアル\(\,\alpha\!\in\!K\,\)が\(\,\sigma\alpha\!\equiv\!\alpha^{N\mathfrak{p}}\:(\mathrm{mod}\,\mathfrak{p})\,\)を満たすような, 有限アーベル拡大\(\,K\!/k\,\)のガロア群\(\,G(K\!\!\:/k)\,\)の元\(\,\sigma\!=\!\displaystyle{\left(\!\frac{\!\:K\!\!\:/k\!\:}{\mathfrak{p}}\!\right)}\,\)(アルティン記号) が定まることをもって, \(K\!\!\:/k\,\)を\(\,k\,\)のイデアル群\(\,\mathfrak{H}(K\!\!\:/k)\,\)に対応する類体とするとき, \(\sigma\,\)は\(\,\mathfrak{p}\,\)が属する\(\,\mathrm{mod}\,\mathfrak{H}\,\)の剰余類のみにより定まり, この対応により\(\,\mathrm{mod}\,\mathfrak{H}\,\)の剰余類と\(\,G(K\!\!\:/k)\,\)が同型となる. ―― 一方, 類体論の価値を認め, 広く知らしめた最初の人物は, アルティンと同年代の若手数学者ハッセ (Helmut Hasse, 1898-1979) であった. 再度 [本田5] から引用する. |
|||
| ハッセが高木の論文のことを知ったのは, 1923年にハンブルクで, アルチンにすすめられてであった. ハッセは高木の第1論文をよむのに, 数週間を要した.「その一般性,
その明晰さ, 効果的な方法とおどろくべき諸結果とに, 深く魅惑された」と筆者に語っている. (中略) ハッセは高木の論文を徹底的に分析究明し, 困難な諸定理の証明を, 独自の方法で整理し, 明快にしていった. …… 1925年 (中略) ドイツ数学者協会年会において, ハルレ大学教授ヘルムート・ハッセ (27歳) は,「類体論の最近の発展について」と題する講演を行い, 高木の理論の大要を紹介した. (中略) ついでハッセは, この講演を敷衍した,「代数体の理論の最近の研究と問題に関する報告」と題するくわしい総合報告を, 協会の年報に3回 (1926, 27, 30年) に亙り発表した. ハッセの独自の整理を行なった, 完全な証明つきの報告である. ハッセの講演と報告は, 高木の類体論を世界の数学界に紹介するのに, 決定的な役割を演じた. |
|||
 E.アルティン (1898-1962) |
 H.ハッセ (1898-1979) |
||
| ここに挙げられている3回の年報報告 ([Hasse 報文]) とは, |
|||
| [Hasse1] "Bericht über neuere Untersuchungen und Probleme aus der Theorie der algebraischen
Zahlkörper. I: Klassenkörpertheorie" Jahresbericht der Deutschen Mathematiker-Vereinigung, Vol.35, 1926, pp.1–55. [Hasse2] "―― Teil Ia: Beweise zu I" J. D. M. V., Vol.36, 1927, pp.233–311. [Hasse3] "―― Teil II: Reziprozitätsgesetz" J. D. M. V., Ergänzungsband Vol.6, 1930, pp.1-204. |
|||
| なる3編の論文を指す. |
|||
| 前者二者 [Hasse1], [Hasse2] は, 貞治の第一論文 [高木13] に関するもので, ハッセ考案による乗法的合同式 ((前出の) 射類\(\,\mathfrak{S}_\mathfrak{m}\,\)の定義で用いた合同式) により類体論の諸定理を証明入りで紹介したものであり, 今後の問題として, | |||
| ・アーベル拡大の構成問題 (ヒルベルトの第12問題 (既出)) ・\(k\,\)の任意のイデアルはその絶対類体\(\!\:K\!\:\)において単項化すること (単項化定理) の証明 ・\(k_{\!\:i}\,\)を\(\,k_{\!\:i+1}\,\)の絶対類体として, \(k\!=\!k_{{}_{0}}\!\subset\!k_{{}_{1}}\!\subset\!\cdots\! \subset\!k_n\!\subset\!\cdots\,\)は有限で終わるか (類体塔の問題) |
|||
| を挙げている. 一方, 後者 [Hasse3] は, ハッセ独自の記法を用いて相互法則を証明したものである. \(k\,\)の素点\(\,\mathfrak{p}\), 乗法群\(\,k^{\ast}\!=\!k\!\:\backslash\{0\}\,\)の元\(\,\beta\), アーベル拡大\(\,K\!\!\:/k\,\)に対し, \(K\,\)は\(\,k\,\)の或るイデアル群\(\,\mathscr{K}\,\)の類体であり, \(\mathscr{K}\,\)の導手\(\,\mathfrak{f}\,\)の素因子分解を\(\,\mathfrak{p}\,\)に関する部分\(\,\mathfrak{p}^{\nu}\!=\!\mathfrak{f}_{\mathfrak{p}}\,\)を用いて\(\,\mathfrak{p}\!=\!\mathfrak{f}_{\mathfrak{p}}\!\:\mathfrak{f}^{\mathfrak{\!\:p}}\,\)とすれば, |
|||
| \(\beta_{{}_{0}}\equiv\!\beta\:(\mathrm{mod}\,\mathfrak{f}_{\mathfrak{p}}),\:\: \beta_{{}_{0}}\equiv\!1\:(\mathrm{mod}\,\mathfrak{f}^{\mathfrak{\!\:p}})\) |
|||
| なる\(\,\beta_{{}_{0}}\!\in\!k\,\)がとれる. \((\beta_{{}_{0}}\!\:)\,\)における\(\,\mathfrak{f}_{\mathfrak{p}}\,\)と無縁な成分\(\,\mathfrak{b}\,\)から定まるアルティン記号\(\,\displaystyle{\left(\!\frac{K}{\mathfrak{b}}\!\right)}\,\)を\(\,\displaystyle{\left(\!\frac{\beta,\!\:K\!\!\:/k}{\mathfrak{p}}\!\right)}\,\)と定義し, 積公式\(\,\displaystyle{\prod_{\mathfrak{p}}\! \left(\!\frac{\beta,\,K\!\!\:/k}{\mathfrak{p}}\!\right)\! =\!1}\,\)(\(\mathfrak{p}\,\)は\(\,k\,\)の全ての素イデアルに亘る) を導出した上で相互法則を証明したのであった. ハッセは, [Hasse 報文] において, 一般相互法則から冪剰余の相互法則も示している. \(1\,\)の原始\(\,m\,\)乗根を含む代数体\(\,k\:\)および\(\,k\!\:(\sqrt[m\!\:]{\alpha\!\:}\!\:)\,\)で不分岐な素イデアル\(\,\mathfrak{p}\!\in\!k\,\)に対し,\(\,1\,\)の\(\,m\,\)乗根\(\,\displaystyle{\left(\!\frac{\!\:\alpha\!\:}{\mathfrak{p}}\!\right)}\,\)を \(\displaystyle{\alpha^{\frac{N\!\:\mathfrak{p}\!\:-\!\:1}{\mathfrak{p}}}\!\equiv\! \left(\!\frac{\!\:\alpha\!\:}{\mathfrak{p}}\!\right)\:(\mathrm{mod}\,\mathfrak{p})}\,\)で定義する. \(k\:\)のイデアル\(\,\mathfrak{a}\!=\!\displaystyle{\prod\mathfrak{p}^{\nu}}\,\)に対して定義される\(\,k\,\)の\(\,m\,\)冪剰余記号 |
|||
| \(\displaystyle{\left(\!\frac{\!\:\alpha\!\:}{\mathfrak{p}}\!\right)}\)\(\displaystyle{= \!\prod\!\left(\!\frac{\!\:\alpha\!\:}{\mathfrak{p}}\!\right)^{\!\!\nu} \!\Longleftrightarrow \left(\!\frac{k\!\:(\sqrt[m\,]{\alpha\,})/k} {\mathfrak{p}}\!\right)\sqrt[m\,]{\alpha\,} =\!\left(\!\frac{\!\:\alpha\!\:}{\mathfrak{p}}\!\right)\sqrt[m\,]{\alpha\,}}\) |
|||
| の値は, \(k\!\:(\sqrt[m\,]{\alpha\,}\!\:)/k\,\)に対応するイデアル群\(\,\mathfrak{H}\,\)の\(\,\mathfrak{a}\,\)の属する剰余類のみで決定され, \(k\!\:(\sqrt[m\,]{\alpha\,}\!\:)/k\,\)と\(\,k\!\:(\sqrt[m\,]{\beta\,}\!\:)/k\,\) の導手が互いに素ならば\(\,\displaystyle{\left(\!\frac{\!\:\alpha\!\:}{\beta}\!\right)\!=\!\left(\!\frac{\beta}{\!\:\alpha\!\:} \!\right)}\,\)である. ―― 結局, 貞治の類体論は, 咀嚼吸収度の高い研究意欲旺盛なドイツの若手数学者達によってその価値を見出され, 改良されつつ徐々に広められていったのである. では, 最初に「類体の構成問題」や「単項化定理」を持ち出したヒルベルトの反応はどうであったか. 『回顧と展望』には |
|||
| ヒルベルトが類體論を讀んだか, 讀まなかつたかハッキリしない. ヒルベルトは, 1898年位から, 例の報文を書いた直後から, 整數論とは離れてゐたのである.
(中略) ところが1925,6年頃に私はヒルベルトから手紙を貰つた. それは私の論文をアンナーレンに轉載することを申込で來たのであつたが, その手紙の中に, ヒルベルトが代數的整數論の講義をするについて,「初めてお前の論文を讀んだ」と書いて, そこの處へ ausführlich と書き入れがしてある. どうも1920年に受取つた論文を25年に初めて讀んだのでは, あまり氣の毒だから,「始めて詳しく讀んだ」ことにしたのであらう. ああ見えても, ヒルベルトは中々細心な所のある人であると思つて, 可笑しかつた. |
|||
| とある. 「アンナーレン」"Mathematische Annalen" とは, [Hilbert2] や [Furtwängler1] などが掲載されたドイツの学術誌である. 講義の題材にしようと考えたくらいであるから, ヒルベルトも貞治の論文を一応は読んだのであろう. しかし, その後, 貞治の論文との関連性においてアルティンやハッセのように目覚ましい活躍を見せた形跡はない. なお,「単項化定理」については, フルトヴェングラーが |
|||
| [Furtwängler4] "Beweis des Hauptidealsatzes für die Klassenkörper algebraischer Zahlkörper" Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg, Vol.7, 1930, pp.14-36. | |||
| において (アルティンの相互法則を用いてこれを群論化した上で) 証明しており, これは [Hasse3] でも紹介されている. フルトヴェングラーが持ち出した「類体塔」の問題は, 後年 (1964年), ゴロッド (Evgeny Golod, 1935-2018) および シャファレヴィチ (Igor Shafarevich, 1923-2017) により否定的に解決された. |
|||
| [本田6] 『高木貞治の生涯』/ 日本評論社『数学セミナー』1975年6月号, p.52. | |||
| からもう少し引用する. |
|||
| フルトヴェングラーのこの成果 (単項化定理の証明) は, 高木の若い弟子弥永昌吉氏によって, 一般の法\(\,\mathfrak{m}\,\)による Strahl 類群 (射類群) 上の類体へと拡張された. やはり1930年のことである. 弥永氏は翌年からヨーロッパに留学して, まずハンブルクでアルチンに師事した. アルチンはちょうど類体論の講義を行なったのであるが, きき手の中に, フランスの青年数学者クロード・シュヴァレイがいた. ある日のこと, シュヴァレイが「類体論の算術的証明ができた」といって, 弥永氏をおどろかせた. (中略) のちに彼はこれをまとめて学位論文とした. (中略) それは高木のあっせんにより, 1933年の東大理学部紀要にのせられた. |
|||
| 彌永昌吉 (1906-2006) は,「旧制大学3年のとき, 高木先生についてこの理論 (類体論) を勉強し, その美しさに打たれた」と |
|||
| [彌永1] 彌永昌吉『類体論とは?』/ 日本評論社『数学セミナー』1975年1月号, p.2. | |||
| において記している. 「高木先生やアルティンの指導を受けて, それに関するいくらかの仕事もした」と述べる彌永は, フルトヴェングラーが示した「絶対類体 (導手1) の場合」を「一般の導手の場合」に拡張し,『帝国學士院紀事』および『日本数學輯報』等に掲載された初期の論文 |
|||
| [彌永2] "Über den Führer eines relativ zyklischen Zahlkörpers" (相対巡回拡大体の導手について) Proc. Imp. Acad. Japan, Vol.5, 1929, pp.108-110. | |||
| [彌永3] "Über den allgemeinen Hauptidealsatz" (一般単項イデアル定理について) Jpn. J. Math. Vol.7, 1930, pp.315-333. | |||
| に著した. [彌永2] では合同イデアル類群の導手における素イデアルの冪の代数的な決定を巡回群に適用すること, [彌永3] では射類群に対する類体を考え基礎体の射類体を決定することを, 各々の考察の主題としている. これは後に群論を駆使した代数的手法で整理 (種の法 Geschlechtermoduln によりこの定理を合同イデアル類体の場合にまで拡張) され,『ハンブルク大学数学誌』および (ドイツの純粋応用数学誌)『クレレ誌』 に |
|||
| [彌永4] "Zum Beweis des Hauptidealsatzes" (一般単項イデアル定理の証明) Abh. Math. Semin. Univ. Hambg. Vol.10, 1934, pp.349-357. | |||
| [彌永5] "Zur Theorie der Geschlechtermoduln" (種の法の理論) J. Reine Angew. Math., Vol.171, 1934, pp.12-18. | |||
| として発表された. 彌永自身が | |||
| 『彌永昌吉先生にお話しを伺う』/ 岩波書店『数学』第44巻第4号 (1992年10月), p.355. | |||
| において「僕のしたもっともきれいな仕事」と述べているものである. |
|||
| §3-6. 類体論の算術的証明 | |||
| 類体論の証明における複雑さは, 貞治自身が「今なお紆余曲折を極め, 人をして倦厭の情を起こさしめる」と述べるほどであった. 貞治の手法は「解析的」な\(\,L\,\)関数が用いられていたが, シュヴァレー (Claude Chevalley, 1909-1984) は (\(L\,\)関数を用いず) イデール群による「代数的」な証明を |
|||
| [Chevalley2] "La theorie du corps de classes" Ann. of Math. Vol.41, No.2, 1940, pp.394-418. | |||
| において示した. 上掲の「弥永氏をおどろかせた」という「算術的証明」は, その時点では完全ではなかったらしい. これに関する彌永自身の述懐を |
|||
| 『仏蘭西の一数学者 — Claude Chevalley のこと—』/ 日佛會館『日佛文科』新第八輯 (1942年7月), pp.235-244. | |||
| から引用する. | |||
| 或日シュヴァレーは私に,「類體論の算術的證明が出來た」と云つて驚かせた. 之は當時懸案の大問題で, 多くの學者が考へてゐたが, その緒に就いて居なかつたのである.
シュヴァレーのそのとき得た證明には, 實は未だ一つ難點が殘され, すつかり算術的にはなつて居なかつたのであつたが, 一般の場合を「圓等分體」の場合に歸着させた彼の方法は素晴しく巧妙なものであつた.
彼は之等のことを纏めて These とし, 丁度1932年, チューリッヒの國際數學者會議に列席の爲渡歐された高木貞治先生と識り合ふ等の機縁もあつて, 高木先生の「類體論」が發表されたと雜誌,「東京帝國大學理學部紀要」に發表した. 彼は後年 (1936) になつて「類體論の算術的證明」を完成した. 叉, 所謂「無限次の場合」をも含む類體論の新しい formulation を得, 算術的な, 詳しい證明と共に1940年に至つて公にした. |
|||
| ここ記された東京帝大理学部紀要 (Journal of the Faculty of Science) に掲載された「学位論文」は,『有限体と局所体の類体論』すなわち |
|||
| [Chevalley1] "Sur la théorie du corps de classes dans les corps finis et les corps locaux" J. Fac. Sci. Imp. Univ. Tokyo, Sect.I, 2, 1933, pp.365-476. | |||
| を指す. これは, 緒言および全十章から成る長大な論文である. 不完全であった算術的証明を完成させた上で「1940年に至つて公にした」論文が, 前出の [Chevalley2] であった. [Chevalley2] の内容を簡潔に記すことは困難であるが, 谷山豊 (1927-1958) の表現を借りれば, 次のように纏められる ( [谷山全集] p.213). |
|||
| \(k_{\mathfrak{p}}\,\)の最大アーベル拡大体の\(\,k_{\mathfrak{p}}\,\)上のガロア群は, \(k_{\mathfrak{p}}\,\)の乗法群の,
適当な位相による completion と同型である (中略). \(k\,\)のすべての素イデアル及び無限素点に対する\(\,k_{\mathfrak{p}}\,\)の直積の適当な部分群\(\,J\,\)で, \(J\!=\!J_0\!\times\!J_{\infty}\,\)と分解される. ここで\(\,J_0\,\)は素イデアル\(\,\mathfrak{p}\,\)に対するもので, 位相的には完全に非連結, 一方\(\,J_{\infty}\,\)は無限素点\(\,\mathfrak{p}\,\)によるもので, 何個かの実数体, 複素数体の乗法群の直積と同型である. (中略) \(k\,\)の最大アーベル拡大体のガロア群\(\,\mathfrak{G}\,\)と商群 (イデール群) \(C\!=\!J\!/k^{\ast}\) (\(k^{\ast}\,\)は\(\,k\,\)の乗法群) との関係を考えると, (中略) \(C\,\)には, \(J_{\infty}\,\)に由来する連結成分\(\,D\,\)がある. (中略) \(\,k_{\mathfrak{p}}\,\)の最大アーベル拡大のガロア群 (\(=\!\mathfrak{G}\,\)における,\(\,\mathfrak{p}\,\)の分解群) と\(\,k_{\mathfrak{p}}\,\)に上記の関係があるが, \(\,\mathfrak{p}\,\)が無限素点のときは, \(k_{\mathfrak{p}}\,\)は総実体又は複素数体だから, その最大アーベル拡大体は\(\,k_{\mathfrak{p}}\,\)上1次又は2次で, この次数は, \(k_{\mathfrak{p}}^{\ast}\,\)における連結成分の次数と等しい. そこで商群\(\,C^{\prime}\!=\!C/D\,\)が\(\,\mathfrak{G}\,\)と同型になることが予想されるが, 事実そうであることが証明されている. これが, イデールの言葉による, 類体論の基本定理である. |
|||
| 彌永昌吉は, シュヴァレーの類体論関連の業績を |
|||
| [彌永6] 『Claude Chevalleyの業績』/ 岩波書店『数学』第15巻第2号 (1963年10月), pp.355-361. | |||
| に詳しく述べている. のみならず, その20年後 (紀寿を迎えんとする直前) にも, やはりシュヴァレーの類体論関連の業績を解説した記事 | |||
| [彌永7] "Travaux de Claude Chevalley sur la theorie du corps de classes: introduction" Jpn. J. Math. Vol.1, 2006, pp.25-85. | |||
| を著して学界を唸らせたのであった. 貞治の類体論とアルティンによる相互法則とをもって, いわゆる「古典的類体論」は完成したが, その後も, \(p\,\)進数の理論との関連性から局所体上の類体論が創設され, 代数関数体における類体論との類似関係などが発見されるなど, 多方面で華々しい研究成果が現れている. 例えば, 上掲の谷山豊は, 高次元アーベル多様体の等分点による虚数乗法論の拡張を目的として |
|||
| [谷山] "Jacobian varieties and number fields", Proceedings of the International Symposium on algebraic number theory, Tokyo-Nikko, 1955, Science Council of Japan, Tokyo, 1956, pp.31-45. | |||
| を著した (この論文は, [谷山全集] pp.57-70 に収録されている). これは, ヒルベルトが1900年にパリ講演で述べた「基礎体を任意の代数体とする類体の構成問題」(「ヒルベルトの23の問題」の中の「第12問題」) に対する一つの方向性を示す研究であり, 総実な代数体上の二次総虚拡大体 (\(\small{C\!M}\,\)体) におけるアーベル拡大の解明に繋がるものであった. 「アアベル体即ち類体」(『代数的整数論』序) なる標語に代表されるように,「古典的類体論」は\(\,k\,\)の素イデアルの\(\,K\!/k\,\)(アーベル拡大の範疇) における素数分解の構造を解明する. これを非アーベル拡大 (\(\mathbb{Q}(\sqrt[3]{2\!\:})\,\)など) に拡張する試み, 即ち「非可換類体論」についても, \(L\,\)関数と保型形式との関連性から多くの成果が得られてはいるものの, 21世紀になって四半世紀を迎えた今年 (2025年, 高木貞治生誕150年) に至るまで, 完全な解決には至っていない. また, \(K\,\)を有限次代数体ではなく有限体上の高い超越次数をもつ関数体へと拡張する試みは,「高次元類体論」の範疇として, やはり多くの綿密な研究が今現在も進められている. この辺りの事情については, |
|||
| [斎藤] 斎藤秀司『高次元類体論の現在』/ 岩波書店『数学』第67巻第3号 (2015年7月), pp.246-270. [加藤] 加藤和也『整数論の近年のいくつかの進展をふりかえって』岩波書店『数学』第69巻第4号 (2017年10月), pp.413-428. |
|||
| に, 興味深い記事が展開されている. |
|||
| 類体論に一応の区切りをつけた貞治は, その後, 学術的には大きな業績を残していない. [高木全集] に収録されたその後の論文は何れも数ページから十数ページの短いものであるが, 彌永が |
|||
| [彌永8] 彌永昌吉『数学者の世界』岩波書店, 1982, p.10. | |||
| に述べている通り「英知が溢れ, その内容は必ずしも「尖端的」でなくても, いずれも数学の根柢に触れるものがある」. |
|||
| [高木18] "On the law of reciprocity in the cyclotomic corpus" (円分体における相互法則について) Proc. Phys.-Math. Soc. Japan, Ser.III, Vol.4, 1922, pp.173-182. | |||
| [高木19] "On an algebraic problem related to an analytic theorem of Carathéodory and Fejér and on an allied theorem of Landau" (カラテオドリ-フェイエールの解析定理に関する代数的問題とランダウによる関連定理について) Jap. J. Math. Vol.1, 1924, pp.83-93. | |||
| [高木20] "Note on Fredholm’s determinants" (フレドホルム行列式に関する注記), Nagaoka Anniversary Volume, 1925, pp.313-318. | |||
| [高木21] "Remarks on an Algebraic Problem" (代数的問題に関するコメント) Jpn. J. Math. Vol.2, 1925, pp.13-17. | |||
| [高木22] "On the mutual reduction of algebraic equations" (代数方程式の相互還元について) Proc. Imp. Acad. Japan, Vol.2, 1926, pp.41-42. | |||
| [高木23] "Zur Theorie des Kreiskörpers" (円分体の理論について) J. Reine Angew. Math. Vol.157, 1927, pp.230-238. | |||
| [高木24] "On the theory of indeterminate equations of the second degree in two variables" (二変数の二次不定方程式論について) Bull. Calcutta Math. Soc. Commemoration Vo.20, 1928, pp.59-66. | |||
| [高木25] "Zur Theorie der natürlichen Zahlen" (自然数論について) Proc. Imp. Acad. Japan, Vol.7, 1931, pp.29-30. | |||
| [高木26] "Zur Axiomatik der ganzen und der reellen Zahlen" (整数と実数の公理について) Proc. Imp. Acad. Japan, Vol.21, 1945, pp.111-113. | |||
| [高木18] は類体論の一つの応用成果として『日本數學物理學會記事』に発表され, カラテオドリ-フェイエールの上掲定理を偶数次元空間凸領域の性質に基いて示した [高木19] および (その続編に当たる) [高木21] は『日本数學輯報』(Japanese Journal of Mathematics) 創刊号および第2巻に掲載された. また, [高木20] は長岡半太郎の退官記念に教え子達が寄稿出版した『東京帝國大學在職25周年記念號』(私家版, 1925)に掲載され, [高木22] は『帝國學士院紀事』に掲載されたものである. [高木23] は, [高木18] の成果をクンマーの正則素数問題に適用したもので, やはり『クレレ』誌に発表された. [高木24] は『カルカッタ数学協会紀要』に掲載されたもので, 二変数二次不定方程式をペル (バースカラ) 方程式へ帰着させる解法を扱っている. また, ペアノとは異なる方法で自然数における結合則と可換則を導出する [高木25] およびその続編である [高木26] は『帝国學士院紀事』に発表された. これらは後に『数学雑談』や『数の概念』に纏められることになるものである. 以上に紹介した [高木1] から [高木26] までは, 論文集 [高木全集] に収録されたものである. 実際には, これ以外にもいくつかの (数ページ程度の短い) 論文が存在する. 何れも, 貞治独特の視点をもって書かれた優れたセンスに富んだ珠玉の逸品と言えよう. |
|||
| §4.著書に見る思想 (1) | |||
| §4-1.『新撰算術』 | |||
| 貞治は, その生涯の大半を数学者 (研究者) および大学教授 (教育者) として過ごした. 教育者としての貞治に関しては次節に回すことにして, 本節では, その両者の立場に基いて創出された著書について見ていくことにしよう. 貞治の最初の著書は, 大学院生時代 (洋行直前) に著した |
|||
| 『新撰算術』帝國百科全書第六編, 博文館, 1898, 全297頁. | |||
| である. 貞治はこのとき23歳であった. 序文を見ると, |
|||
| 「アリスメチック」ノ語ニハ二樣ノ意義アリ. (中略) 前者ヲ算術ト稱シ, 後者ヲ整數論と云フ (中略) 本書説ク所ハ, 此所謂算術ニ外ナラズ. (中略) 此書ノ眼目トスル所ハ, 讀者ヲシテ數ノ精確ナル觀念ヲ得セシメントスルニアリ. 抑々數學ニ於ケル數の觀念カ十分明晰ニ説明セラレ, 最嚴密ナル意味ニオ於テ論理的ニ完全ノモノナレルハ, メテ輓近ノ事に屬ス. (中略) 此智識は高等數學ヲ修ムルノ階梯トシテ, 欠くヘカラサル者ナリ. |
|||
| とある. 要するに, 小学校時代から慣れ親しんだ「数」を一度精密に見直し, 高等数学を学ぶ確固たる基礎固めを目的としている. 対象とする読者は明記されていないが, 恐らく, 初等教育に携わる教員か学部生または大学院生であろう. 全6章49節から成る書籍で, その内訳は |
|||
| 第一章 整数 (整数の四則演算, 冪乗, 合同式) 第二章 整数の性質 (公約数と公倍数, 素因数分解, \(\varphi(m)\,\)の性質, フェルマーの小定理) 第三章 分数 (分数と小数の四則演算, 加比の理, 循環小数と循環節) 第四章 冪根 (冪乗と冪根, 有理数の限界, 開平算) 第五章 無理数 (数列または有理数の切断による無理数の定義, 無理数の大小と四則演算) 第六章 量及其測定 (量の相等と大小関係, 量の連続性, 量の測定, 長さ・面積・体積) 結 論 負数, 虚数および実数, 代数学の基本定理 |
|||
| となっている. 丁寧な解説であるが, 緻密な議論を積み重ねるため, 全てを精密に読むには根気がいる. 決して読みやすい著作ではないが, 数学の根柢を形作る数の大系が過不足なく展開されている著作である. 『新撰算術』は「帝國百科全書」なるシリーズの中の一冊に収められた. 本文の後に掲載された宣伝文句を見ると,「全部壱百卷, 紙數壱册壱三百廿頁, 毎月壱回發行」とあり, 発刊の主旨として「専門學述の普及を促して已まず, 本書は乃ち此急需に應じて起りたる者にして, 會智識の指導を以て任ずる者, 獨り僻郷師に乏しき者の爲のみとせんや, 大都大中學に在るの士も, 亦本書に俟つ所必ず多大なる者あらん」と書かれている. この向学心に満ちた出版社 (博文館) の意気込みと, 狭窄的な営利中心主義に傾く現今の出版業界とを想うとき, 甚だしき隔世の感を否めない. |
|||
| §4-2.『新撰代数学』 | |||
| その「帝國百科全書」には貞治の2冊目の著書 |
|||
| 『新撰代數學』帝國百科全書第十七編, 博文館, 1898, 全296頁. | |||
| も収録された. これも貞治が23歳のときの著作である. |
|||
 『新選算術』(博文館, 1898) |
 『新選代数学』(博文館, 1898) |
||
| これは前作『新撰算術』の続編とも言うべき著作であり, この頃 (即ち貞治が『あーべる方程式ニツキテ』を書いた頃) に繙いたであろう [Serret1], [Serret2], [Weber1] の内容と重複するものである. 全9章64節から成る書籍で, 内訳は |
|||
| 第一章 序論 (演算, 実数, 数の大小関係, 虚数とその幾何学的表示) 第二章 有理関数 (四則演算, 二項定理, 剰余の定理, 最大公約, 有理関数, 導関数とテイラー展開) 第三章 方程式の根 (複根, 整関数の連続性, 根の存在, ラグランジュの補間法) 第四章 整関数の有理分解 (関数の可約と既約, ガウスの補題, アイゼンシュタインの定理) 第五章 多変数関数 (多変数関数の同次性, 項の数, 分解, 展開) 第六章 対称式論 (冪和, 対称式の基本定理, 交代式, 判別式, 終結式, チルンハウス変換) 第七章 行列式 (行列式の性質, 小行列式, 行列式の積, 連立方程式, 補間法) 第八章 二次形式論 (二次形式の行列式, 二次形式の平方和への変形) 第九章 三次および四次方程式 (カルダノの解法, 四次方程式の解法, チルンハウス変換, ラグランジュの解法) |
|||
| となっている. |
|||
| 『新撰代數學』は, 前作の『新撰算術』と異なり, 序文に該当するものがない. そのため, 執筆目的は不明であるが, 貞治の恩師である藤澤利喜太郎が後年に発表した報告書 | |||
| [藤澤] "Summary Report on the Teaching of Mathematics in Japan" 文部省, 1912. | |||
| によれば (Chap.VII "The teaching of mathematics in higher middle schools"),
東京高等師範学校 (1886年設立) および広島高等師範学校 (1902年設立) の第2学年において『新撰代數學』が教科書として用いられたという. ところで,『新撰代數學』の序論の第一節には |
|||
| 代數學ニ於ケル硏究ノ主眼トナルヘキモノハ, 數ノ値即其大小ニ關係スル者ニアラスシテ, 寧ロ數ノ算法ニ關係スルモノナリ. 算法トハ畢竟一定ノ順序ニ與ヘラレタル二個ノ數ヨリシテ,
新ニ第三ノ數ヲ定ムル方法ニ外ナラズ. 代數學ニ於テ用ヰラルヽ算法は所謂加減乘除ノ四則ニ限レリ. 吾輩ハ此處ニ此四則算法ヲ支配スル根原的ノ法則ヲ略叙シ, 讀者ノ記臆ヲ新ニシ, 以テ新硏究ノ地ヲ成サント欲ス. |
|||
| とある. ここでも, 数学の根柢となる数の演算構造を厳密に構築しようとする貞治の姿勢が如実に窺えよう. その後, 代数学全般に亘り綿密なる議論が展開された後, 第九章の最終節において, 貞治の代数学に対する思想が再び明確に表現される. |
|||
| 方程式ノ代數解法ハ代數學ニ於テ最重要ナル問題ニシテ, 代數學ハ其實方程式ノ硏究ニ外ナラスト謂フモ過言ニアラサルナリ. 四次以下ノ方程式ノ解法ハ十五六世紀の交旣ニ以太利ノ學者間ニ知ラレタル所ナレトモ, 其解法ハ個々其趣ヲ殊ニセリ. ラグランジュハ此等ノ解法ノ根柢ニ一貫セル系統ノ潜在セルヲ看破シタル後, 更ニ此一貫ノ經路ヲ尋ネテ五次以上ノ方程式ノ解法ヲ索メタレドモ其効ヲ奏セザリキ, 今日ニ於テハ, 五次以上の一般ノ方程式ノ代數的解法ハ絕對的ニ不可能ノ事ナルコト旣ニ證明セラレ方程式ノ硏究ハ別に新進路ヲ採ルに至レリ. 此最モ趣味饒キ硏究塲裡ニ入ルニ及バズシテ茲ニ讀者ニ辭セサルヲ得サルハ吾輩ノ最も憾トスル所ナリ. 讀者若シ更ニ進テ現今代數學ノ眞相ヲ究メント欲セハ請フ去テウェーバー敎授ノ有名ナル敎科書 (H. Weber, Lehrbuch der Algebra) を繙ケ. |
|||
| 洋行直前,『あーべる方程式ニツキテ』を完成させた貞治が最も関心を抱いていた代数方程式論の最先端を, この著作において一般読者に示唆したのであった. 『新撰代數學』は, 日本人著者による最初の本格的な代数学の専門書と言えよう. |
|||
| §4-3.『新撰算術講義』 | |||
| 洋行を経て帰朝した後, 1904年に東京帝大教授に就任した貞治は, 同年, | |||
| 『新式算術講義』博文館, 1904, 全436頁. | |||
| を上梓した. このとき貞治は29歳であった. 当然のことながら, 前二作の表紙にある「理学士」なる記載が, ここでは「理学博士」に書き替わっている. |
|||
 『新式算術講義』(博文館, 1904) |
 『新式算術講義』(ちくま学芸文庫, 2008) |
||
| この著作の執筆目的は「緒言」に明記されている. |
|||
| 算術敎師が算術の知識を求むる範圍, 其敎ふる兒童の敎科用書と同一程度の者に限らるゝこと, 極めて危殆なりと謂ふべし, 確實なる知識の缺乏を補ふに, 敎授法の經驗を以てせんとするは,「無き袖を振はん」とするなり. 又数學を專攻せんとする學生にありても, 目下の狀態に於ては, 其算術の知識は幼時普通敎育によりて得たる所に限られ, 漸く進んで稍々高等なる数學諸分科の修業に入るに當りても, 數學の根源に關せる問題を囘顧して, 精密に之を復習するの遑なきが如し. 斯の如くなれば其知識は堅牢なる地盤を缺くが故に, 學ぶ所愈々進むに随ひ, 知る所愈々不確実となる. |
|||
| 小学校以来, 充分に理解したと思っていた事柄が実はそうでなかったという例は少なくない. 例えば, 中学生や高校生であっても, 小学校の範囲である「\(a\!\div\!b\,\)が\(\,a\!\times\!(1/b)\,\)に等しい」ことの説明ができないという事例は (少なくとも私の携わる教育現場では) 多々見られる. 中学校におけるユークリッド幾何, 高等学校における三角関数や微積分などが, (その出立点において) 直観や厳密性に欠ける前提に基いて構成されていることも (教員側にとっては) 周知の事実である. 貞治は, このような事柄に関して, 再度顧みて精密に理解せよと注意を喚起したのである. 『新式算術講義』は全11章から成り, 内容は |
|||
| 第一章 自然数の起源 (順序数, 基数, 自然数の公理) 第ニ章 四則算法 (可換律, 結合律, 分配律, 除法の原理, 冪乗, 2数の最高位の係数および桁数の比較) 第三章 負数, 四則算法の再審 (数学的帰納法の原理, 負数の演算法則, 絶対値) 第四章 整除に関する整数の性質 (合同式, 不定方程式, 算術の基本定理, 素数の無数性) 第五章 分数 (既約分数, 有理数の稠密性, 比例式, 有理数の四則演算) 第六章 分数に関する整数論的の研究 (部分分数分解, \(\varphi(n)\,\)の性質, フェルマーの小定理) 第七章 四則算法と形式上不易 (数が従うべき一般的な演算法則, 除法の例外) 第八章 量の連続性及無理数の起源 (量の比較, 有理区域に属する量, ユークリッドの比例論) 第九章 無理数 (上限と下限, 有理数の稠密性, 有理数の切断, 無理数の四則演算) 第十章 極限及連続的算法 (極限, 集積点の存在, 基本列, 連続的算法の定義と拡張) 第十一章 冪及対数 (冪乗の存在と極限, 有理数の指数, 無理数の指数, 開平算) |
|||
| である. 藤澤がその著書『算術條目及敎授法』(1895) ,『算術敎科書』(大日本圖書, 1896) において, 算術から量の概念を除外しようとしたのに対し, 貞治は積極的に量およびその連続性を扱っている. また, 統計学にも造詣が深かった藤澤は, 上掲書において, 歩合算や利息算や年金算などを採り入れ, その関係から級数や対数をも扱っていた. それを意識したのであろうか, 貞治も『新式算術講義』において, 極限や対数など解析的な内容を「算術」に含めているのである. 些細なことであるが, 貞治は『新式算術講義』第六章において, 現今ではオイラーの関数 "Euler's totient function" として知られる\(\,\varphi(n)\,\)を「ガウスの函数」(p.174) あるいは「ガウスは\(\,\varphi(n)\,\)なる記號を用ゐたり」(p.197) と述べている. 前作『新撰算術』の第ニ章 (pp.89-100) では\(\,\varphi(m)\,\)に関して固有名詞は登場しないが,『初等整数論講義』(後述) の第一章 (p.41) では「Euler の函数\(\,\varphi(n)\,\)」として紹介されている. 貞治が如何なる理由でガウスの名を挙げたのか, 出典が気になるところである. 数学の専門書でありながら縦書きを余儀なくされる和製数学書のスタイルには, 貞治も辟易したことであろう. 巻末の「附録」には, |
|||
| 「フート, ノート」といふもの邦文の書に入り難し. 本文の各處に添ふべき重なる引用及參照書目を取りまとめて, 卷末に附するに當り, 印刷の進行中に心つきたる本文の修正追補ニ三を收む. | |||
| とある. |
|||
| 15ページに亘るこの (当時としては珍しい)「脚注」から, 興味深い記述を少し抜粋してみよう. |
|||
| 「代數的の數」(中略) につきて注意すべき一條あり. 古風の數學書又は通俗數學書 (特に或種の初等敎科書) 等に於て此語を負數又は所謂不盡冪根などの義に用ゐたる者なきを保せず. 然れども斯の如きは當今の數學社會一般に用ゐらるゝ用語例を違犯せる者なり. (中略) | |||
| Dの右及左に如何なる點をとるとも, 其中間には必點 (Dより外の) あり. Dの直に右, 直の左の點なる者なし. 連續の定義はデヾキンドの名著, 連續及無理数 (Dedekind, Stetigkeit und Irrationale Zahlen, 1872) に載す. これ必讀の書なり. (中略) | |||
| 此書に於てはデヾキンドの連續の法則を採りて, アキシオマチツクの方法に準じ以て數の觀念を說明せり. 但本邦の一般讀書界の程度を顧慮して, 形式的に論理の最嚴密なるを期せざりき. | |||
| 上記の諸書に於ける叙述の調子槪して全く量の觀念を離れ, 最抽象的に卒然として無理數の定義を立し數と量との關係は讀者の推考發明に一任せり. 而し讀者の多數は其自ら補充すべき所の者を自ら補充することをせずして, 之を說明の不明に歸せしめんとするの傾向を有するが如し. | |||
| 此種の叙述は論理上間然する所なしと雖, 一般讀者の讀書力を信用すること多きに過ぎたりと謂ふべし. 予の舊著「新撰算術」に於ても紙幅節儉の爲此種の叙述法を採りたり. (中略) | |||
| 上掲の引用部では割愛したが, 貞治はこの「脚注」において, \(4k\!+\!1\,\)あるいは\(\,6k\!+\!1\,\)なる形の素数が無数に存在することを巧妙に証明している. また, 無理数の定義についても, 無限小数を拡張するヴァイエルシュトラスの手法を簡明に説明している (本文では基本列数によるカントールの方法や有理数の切断によるデデキントの方法も紹介されている). なお, この「脚注」の後には,「學用語對譯」として, |
|||
| エラトステネスの篩 sieve of Eratosthenes, crible d'Eratosthène. 集積點 Häufungsstelle, Verdichtungspunkt, point limit. 不定方程式 indeterminate equation, unbestimmte Gleichung. |
|||
| など, 和語と英語ないし独語の対訳が付されている. これも, 読者の便宜を図ってのことであるが, これを掲載することは, 当時の和製数学書としては初めてに近い試みであったと言えよう. |
|||
| §4-4.『普通教育代数教科書』 | |||
| 『新式算術講義』を著した貞治は, その後, 東京帝国大学理科大学教授 (理学博士) としての執筆義務を負ったか, あるいは執筆依頼を受けたかなどの経緯により, 多くの教科書を執筆した. |
|||
| [追想高木] 河田敬義編『追想 髙木貞治先生』高木貞治先生生誕百年記念会, 1986. | |||
| の巻末にある「著作目録」を見ると,「著あるいは編著」のリスト | |||
| 『普通教育算術教科書』,『普通教育代数教科書』(1904) 『女子教育算術教科書』,『女子教育代数教科書』,『女子教育幾何教科書』(1907) 『廣算術教科書』(1909) 『師範教育数学教科書 [算術・代数]』(1910) 『師範教育数学教科書 [平面幾何・立体幾何]』,『新式算術教科書』,『新式代数教科書』,『新式幾何教科書 [平面・立体]』,『新式三角法教科書』(1911) |
|||
| が掲載されている. 出版社は何れも開成館である. 「普通教育」や「新式」は旧制中学校および高等学校で,「女子教育」は高等女学校で,「師範教育」は高等師範学校で採用されていたものと思われる. このリストの中の教科書から下記の二冊を繙いてみよう. 因みに, これら教科書類は全て横書きで書かれている. まず,『普通敎育代數敎科書』を見ると, 冒頭の「例言」すなわち序文には, |
|||
| 普通敎育に於ける代數學敎授の目的は, 生徒をして文字を使用して卑近なる問題を自由に解釋する能力を取得せしむるを以て足れりとすべし. 是故に嚴密なる抽象的の論證は此書の最も忌避する所にして, 常に算術を囘顧して應用上の問題を明透集密に處理することは, 其の最も力を致せる所なり. |
|||
| とある. 前作の『新式算術講義』が教師用として理論構築の厳密性を重視したものであったのに対し, 本作は普通教育の生徒用として厳密性よりも実用的運用力の向上を企図したというのである. 貞治の教育に対する姿勢の一斑が窺えるであろう. この教科書は, 上下二冊に分冊されている. 上巻の内容は現今の中学校から高等学校初学年にかけての内容 (整式の四則演算 (ただし除法は単項式に限る), 因数分解, (連立を含む) 一次方程式) であり, 下巻は現今の中学校高学年から高等学校全般にかけての内容 (二次方程式, 分数式, 冪根, 対数, 級数, 順列と組合せ, 二項定理) になっている. 何れの巻末にも補習問題がちょうど150題ずつ付されている. 例えば, 上巻の問題は |
|||
| 6. 四時四十八分ニハ時計ノ短針ハ長針ヨリモ幾分畫ダケ後ニアルカ. 叉\(\,m\,\)時\(\,n\,\)分には如何. | |||
| 55. 或試驗ノ受驗者二百六十人ニテ, 受驗者全體ノ平均點數64, 及第者ノ平均點數67, 落第者ノ平均点數57ナリ. 及第者及ビ落第者各〃幾人ナルカ. | |||
| 116. 次ノ方程式ヲ解ケ. \((b\!-\!c)(x\!-\!a)\!+\!(c\!-\!a)(x\!-\!b)\!+\!(a\!-\!b)(x\!-\!c)\!=\!d\) | |||
| 149. 七圓七十錢ノ買ヒ物ヲナシ十圓紙幣ヲ出シテつり錢ヲ取リタルニ, 二十錢, 十錢, 五錢ノ三種ノ貨幣合セテ二十四枚ヲ得タリ. 此中, 白銅貨ノ數ハ二十錢銀貨ノ數ノ二倍ナリシト云フ. つり錢ノ勘定ニ誤リナカリシカ. | |||
| などであり (各問の冒頭の数字は問題番号を表す), 下巻の問題は | |||
| 184. 次ノ方程式ヲ解ケ. \(1\!-\!x\!=\!\sqrt{1\!-\!x\sqrt{4\!-\!7x^2\!\:}\!\:}\) | |||
| 224. \(\alpha,\beta\,\)ガ二次方程式\(\,x^2\!+\!px\!+\!q\!=\!0\,\)ノ二ツノ根ナルトキ, \(\displaystyle{\frac{\,p\alpha\!+\!2q\,}{2\beta\!+\!p}}\,\)ヲ簡單ニセヨ. | |||
| 262. 兵數ノ比\(\,A\!:\!B\,\)ナル東西兩軍ガ交戰シタルニ, 戰死者ノ數の比ハ\(\,a\!\!\::\!\:\!b\), 生還者ノ數ノ比ハ\(\,c\!\!\::\!\:\!d\,\)ナリシト云フ. 兩軍ニ於ケル戰死者ト生還者トノ比各〃幾許ナルカ. | |||
| 294. \(x\,\)ヲ含メル整式ノ五乘冪ヲ計算シテ, 之ヲ\(\,x\,\)の降冪ニ排列セルニ, 其始ノ二項ハ\(\,x^{10}\!\!-\!5x^9\,\)ニシテ, \(x^8\,\)の項ハナシ. 第四項以下ヲ書キ添ヘヨ. | |||
| などである. 現今の教科書に見られるような (解法パターンの定まった) 紋切型の問題の羅列ではなく, 一問一問に対して丹念に取り組みたくなるような独自性の強い問題が数多く含まれている. 尤も,「普通教育」とは言え, 当時の中学校は義務教育ではなく経済的にも学力的にも選ばれた学生のみが進学し得た場所であったことは考慮されねばならない. |
|||
| §4-5.『広算術教科書』 | |||
| 次に,『廣算術教科書』を見てみよう. これも上下二冊に分冊されている. 上巻の内容は |
|||
| 第一篇 緒論 第ニ篇 四則 (加法, 減法, 乘法, 除法, 四則の應用) 第三篇 諸等算 (長さ, 面積, 体積, 重さ, 時間, 貨幣などの単位, 単位の変更と演算) 第四篇 整数ノ性質 (約数, 倍数, 倍数判定, 素数, 素因数分解, 最小公倍数, 最大公約数) 第五篇 分数 (分数の四則演算, 循環小数) |
|||
| であり,下巻の内容は | |||
| 第六篇 比及ビ比例 (比例, 複比, 連比) 第七篇 歩合及ビ利息 (合計高, 残高, 単利法, 複利法, 租税, 保険, 公債, 株式, 手形, 年金) 第八篇 開法 (平方根, 開平算, 無理数, 不盡根数, 立方根) 第九篇 求積 (矩形, 平行四邊形, 梯形, 三角形, 直角三角形, 円, 直方体, 柱体, 円柱, 角錐, 円錐, 球) 第十篇 省略算 (近似値, 省略寄セ算, 省略引キ算, 省略掛ケ算, 省略割リ算, 省略開平) |
|||
| である. 何れも各項目ごとに例題や問題が豊富に掲載され, 巻末には略解が付されている. 序文が存在しないため, 執筆意図や対象読者は不明であるが, 商業系の内容を含む実用性を追求した教科書と言えよう. 上巻第三篇には, |
|||
| 佛國ぱりーノ萬國めーとる同名度量衡局ハめーとる法の物指及ビ分銅ノ原器ヲ保管ス. 物指ノ原器ハ白金製ノ棒ニシテ, 攝氏零度ノ溫度ニ於ケル此棒ノ兩端ノ間ノ長サヲめーとるトイヒ,
之ヲ長サノ單位トス. 一めーとるハ地球子午線ノ長サノ約四千萬分ノ一ニ等シ. 分銅ノ原器モ亦白金ニテ作リ, 其目方ハ大約一めーとるノ十分ノ一ヲ一邊トセル立方體ト同ジキ體積ノ蒸餾水ノ攝氏四度ニ於ケル目方ニ等シ. 此目方 (一きろぐらむ) ノ千分ノ一ヲぐらむト名ヅケ, 之ヲ目方ノ基本單位トス. |
|||
| のように度量衡の万国共通の単位の定め方の記載や (pp.149-150), | |||
| 地球ガ太陽ヲ一週スル時間ハ三百六十五日五時四十八分四十六秒 (365.2422日) ナリ. サレバ一年ヲ365日トスルトキハ, 此端下0.2422日ガ積リテ,
四年ニハ0.9688日即チ約一日トナル. 故ニ四年目毎ニ366日ノ閏年ヲ置ク. サレド, 是ニテハ四年毎ニ 1-0.9688=0.0312日ダケ多過グルガ故ニ, 四百年ノ後ニハ約三日ノ差ヲ生ズ. ヨリテ四百年ノ中ニ三度閏年ヲ省クナリ. (カヤウニスルトキハ四百年中ニ0.12日ノ狂ヒヲ生ズレドモ, 是ガ積リテ一日ノ狂ヒニナルハ約四千年ノ後ナルベシ). |
|||
| のような閏年の定め方の記載 (p.171) も見られる. 下巻にも, 租税 (所得税, 営業税, 関税, 府県税, 市町村税) や株式 (配當歩合,
利廻りなど) に関する詳しい説明があり, 読んでいて大変に面白い. |
|||
| §4-6.『高等教育代数学』 | |||
| 『新式算術講義』を上梓したのと同年の1904年に, 貞治は |
|||
| 『髙等敎育代數學』東京開成館, 1904, 全404頁. | |||
| を上梓した.『新式算術講義』で解明された初等的な算術から, 本格的な代数学へと一歩進んだ内容をもつ講義式の数学書である. |
|||
 『高等教育代数学』(東京開成館, 1904) |
|||
| 序文によれば, |
|||
| 此書ハ (中略) 普通敎育ノ程度以上ニ於テ, 初等代數學ノ一部分ヲ說カントスルモノナリ. 然レドモ取材ノ範圍ハ初等敎育ニ所謂代數學ノ埒外ニ逸スルコトナク,
唯少シク論證ヲ嚴密ニシ, 問題ノ解釋ヲ詳細ニセル點ニ於テ, 稍是ニ凌駕セルニ過ギズ. 純正代數學ノ智識ト趣味トノ本邦數學界ニ普及センコトハ, 編者ノ切望スル所ナリ. |
|||
| とある. その後の文脈から判断すれば, 前掲の「教科書」類における「代数」と西欧数学界にて称される "Argebra" とはレヴェルおよび内容の異なるものであり, この書籍はその階梯的役割を担うと述べているのである. 内容は, |
|||
| 第一篇 緒論 (整式と四則, 展開と因數分解, 対稱式と交代式, 齊次式, 分數式, 複素數) 第ニ篇 一次方程式 (聯立一次方程式を含む) 第三篇 二次方程式 (聯立二次方程式を含む) 第四篇 不等式 (不等式の原則と解法, 絕對不等式, \(n\,\)次不等式, 分數不等式, 極大極小) 第五篇 代數式の數値の變動 (一次函數, 二次函數, 分數函數, 方程式の根の變動) |
|||
| であり, 一見すると前掲「教科書」類と差異がないように見える. しかし, この書籍を繙くと, ここには随所に貞治の数学思想が鏤められ, 扱われる題材も学生への有意義な示唆に富んだものが多いことに気づかされるのである. 例えば, 交代式の項目において, 辞書式順序で |
|||
| \(\,ab\!+\!ac\!+\!bc\,\)あるいは\(\,(a\!-\!b)(a\!-\!c)(b\!-\!c)\,\) | |||
| と表記すべきところを | |||
| \(\,bc\!+\!ca\!+\!ab\,\)あるいは\(\,(b\!-\!c)(c\!-\!a)(a\!-\!b)\,\) | |||
| と表記することには「特別ノ理由アリ」とする (pp.32-33). 即ち, \(bc,\,ca,\,ab\,\)以外の文字 (\(b\!-\!c,\,c\!-\!a,\,a\!-\!b\,\)以外の文字) が順次\(\,a,\,b,\,c\,\)となるように配置するというのである. また, 上式の各々において\(\,ac,\,a\!-\!c\,\)ではなく\(\,ca,\,c\!-\!a\,\)と表記することに関して, |
|||
| コハ所謂循環ノ順序ニシテ次の圖ヲ參照シテ其意義ヲ覺ルベシ. | |||
 |
|||
| とした上で, | |||
| \(a^2(b\!-\!c)\!+\!b^2(c\!-\!a)\!+\!c^2(a\!-\!b)\,\) | |||
| を表記するに際して, 第ニ項のみ負号を用いて | |||
| \(a^2(b\!-\!c)\!-\!b^2(a\!-\!c)\!+\!c^2(a\!-\!b)\,\) | |||
| と表記することは「錯雜セル幼稚ナル記法」と断じている. 貞治は続けて次のように述べる. | |||
| 此處ニ言ヘル如キコトハ, 決シテ拘泥スベキコトニアラズ, 叉一見甚タ些細ナルニ似タリト雖, カヽル些細ナル點ニツキテモ意ヲ用ヰルヘキ餘地アルコトハ, 篤學ノ士ノ注意ヲ要スル所ナルヘキカ. 是ニ於テ吾人ハ我讀者ト共ニ次ノ宣言ヲナスベシ: 代數學ニ於テ數ヲ表ハスニハ, 如何ナル文字ヲモ用ヰ得ヘキ自由アリ. 宜シク此自由ヲ善用シテ, 記法ノ成ルヘク便利ニ, 成ルベク明透ナルヲ勉ムヘキナリ. |
|||
| 数を表す文字に関する貞治の思想は, 後述する『初等整数論講義』においても現れる (p.277) . |
|||
| また, 分数式の通分と見れば直ちに最小公倍数 (式) を持ち出す学生への戒めを | |||
| 最小公分母ニ通分スヘシトイフ普通ノ規則ノ如キハ, 唯凡テノ場合ニ通用スヘキ一種ノ簡便ナル計算ノ方法ニ過ギズ. (中略) 必スシモ其勞ヲ償フニ足ルノ利益ヲ與フルモノニ非ズ. 理論ノ根本ニ屬スル事ト, 計算ノ枝葉ニ關スル事トハ截然區別セラルベキナリ. | |||
| のように与え, 実例として | |||
| 例一. \(\displaystyle{\frac{1}{\!\:x\!+\!a\!\:}\!+\!\frac{1}{\!\:x\!+\!3a\!\:} \!+\!\frac{1}{\!\:x\!+\!5a\!\:}\!+\!\frac{1}{\!\:x\!+\!7a\!\:}}\) |
|||
| 例ニ. \(\displaystyle{\frac{b}{\!\:a(a\!+\!b)\!\:}\!+ \!\frac{c}{\!\:(a\!+\!b)(a\!+\!b\!+\!c)\!\:}\!+\!\frac{d} {\!\:(a\!+\!b\!+\!c)(a\!+\!b\!+\!c\!+\!d)\!\:}}\) |
|||
| 例三. \(\displaystyle{\frac{\!\:x\!-\!1\!\:}{x\!+\!1}\!-\!\frac{\!\:x\!-\!2\!\:}{x\!+\!2} \!-\!\frac{\!\:x\!-\!3\!\:}{x\!+\!3}\!+\!\frac{\!\:x\!-\!4\!\:}{x\!+\!4}}\) |
|||
| を簡約させる問題を掲げている (pp.37-39). 貞治が与えた解法は, 一切の無駄がなく鮮やかで美しい. これらの問題は, 20世紀半ば以降の大学入試問題にたびたび登場するようになる. 恐らく, 貞治の時代の教科書や数学書を出典とするものであろう. その後, 貞治が「をぃらーノ公式」と命名する |
|||
| \(E(0)\!=\!E(1)\!=\!0,\:E(2)\!=\!1,\:E(3)\!=\!a\!+\!b+\!c\). ただし, \(\displaystyle{E(k)=\frac{a^k}{\!\:(a\!-\!b)(a\!-\!c)\!\:}\!+ \!\frac{b^k}{\!\:(b\!-\!c)(b\!-\!a)\!\:}\!+\!\frac{c^k}{\!\:(c\!-\!a)(c\!-\!b)\!\:}}\). |
|||
| が紹介される (p.39). 後述する『代数学講義』においては, より一般化された形で "Eulerの公式" として紹介されるものである (p.65). 以下, 興味深い応用例が種々示されるのであるが, この部分は, 他書には見られない貴重な資料と言えよう. 貞治自身, この「オイラーの公式」に少なからず魅了されたのであろう, 巻末の練習問題にも, この公式に纏わる応用問題が複数掲げられている (pp.363-364). また, 分数式における分母の有理化の項において, |
|||
| 根式ノ根ヲ含メル式, 例ヘバ |
|||
| \(1\!-\!\sqrt{\!\:1\!-\!\sqrt{x\,}},\:\: \sqrt{\!A\!+\!\sqrt{\!B\!+\!C\sqrt{\!\!\:R\,}}}\) |
|||
| 等ヲ組織的ニ論センコトハ, 根ガ平方根ノミニ限レル場合ニ於テモ, 仍ホ高等代數學ノ領域ニ屬セル者トナサヾルベカラズ. | |||
| と注意を与えている (p.51).『新式代數敎科書 續卷』(開成館, 1916) の巻末に掲載されている問題 (p.127) | |||
| 73. 次ノ根數ノ分母ヲ有理化セヨ. (1)\(\,\displaystyle{\frac{\sqrt[3]{6\!\:}}{\!\:\sqrt[3]{3\!\:}\!-\!\sqrt[3]{2\!\:}}}\:\: \) (2)\(\,\displaystyle{\frac{1}{\!\:1\!+\!\sqrt[3]{2\!\:}\!+\!\sqrt[3]{4\!\:}}}\) |
|||
| などと併せ, これらの問題がガロア理論に支配されることを示唆しているのである. |
|||
| さて,『髙等敎育代數學』における方程式および不等式の項目では, 現今の教科書や参考書ではまず扱われないような多岐に亘る問題や解法が紹介され, 読者を惹きつけて飽きさせない魅力に富んでいる.
例えば, 最も単純な一元一次方程式の解法の解説用として, |
|||
| 例一. \(\displaystyle{\frac{x\!+\!1}{2}\!+\!\frac{2x\!-\!1}{3}\!-\!\frac{3x\!-\!2}{4} =\frac{2(5x\!-\!4)}{6}\!-\!\frac{7x\!+\!6}{12}\!+\!3x\!-\!1}\) |
|||
| 例ニ. \(\displaystyle{\frac{a^2(b\!+\!c\!-\!x)}{(a\!-\!b)(a\!-\!c)} \!+\!\frac{b^2(c\!+\!a\!-\!x)}{(b\!-\!c)(b\!-\!a)} \!+\!\frac{c^2(a\!+\!b\!-\!z)}{(c\!-\!a)(c\!-\!b)}=x\!-\!(a\!+\!b\!+\!c)}\) |
|||
| の2題が掲げられ, その一般的解法が示される. その後「一元一次方程式ノ一般ノ解法ハ上ノ如シ. サレド特別ノ工夫ニヨリテ, 解法ヲ短縮シ得ベキ場合多々之アリ.」と述べて | |||
| 例一. \(8(x\!+\!1)\!-\!3(x\!+\!1)=16\!+\!x\) 例ニ. \(\displaystyle{\frac{x\!-\!3a}{4}\!+\!\frac{x\!-\!4a}{5}=\frac{x\!-\!2a}{3} \!+\!\frac{x\!-\!5a}{2}\!-\!\frac{41}{60}a}\) 例三. 五個ノ相連續セル整數ノ和40ニ等シ. 此等ノ數ヲ求メヨ. 例四. \((x\!-\!a)^3\!+\!(x\!-\!b)^3\!+\!(x\!-\!c)^3=3(x\!-\!a)(x\!-\!b)(x\!-\!c)\) |
|||
| の4題が掲げられ, その解説において貞治流の (やや技巧的な) 鮮やかで美しい解法が開陳されるのである. 単に正答を得ればよいのではない, 解法は単純明快を旨とせよと, 学生に注意を与えているわけである. また,「逆數方程式」(と貞治が称するところの相反方程式) が解説された後, その「應用トシテ最重要ナルハ,1ノ冪根ヲ求ムル方程式ナリ」として, 1の\(\,n\,\)乗根 (\(n\!=\!3,6,12,4,8,5\)) に関して懇切丁寧に解説される (pp.188-195). 少しでも多くの学生を「ガロア理論」ないし「アーベル方程式」の魅力へと早く近づけたいという貞治の想いが垣間見える. 不等式の最後の項目にある「極大極小」は, 微分を用いない (絶対不等式あるいは実数条件のみに依拠する) 最大値最小値の問題が扱われ, 第五篇「代數式ノ數値の變動」では, 方程式不等式の幾何学的解法および関数の最大値最小値 (関数のグラフによる) が扱われる. 後半の「方程式の根の變動」では, 二次方程式の三項のうち一つまたは二つの係数が変動する場合の根の変動について解説され, 特に各係数が特定の変数の一次式となる場合の根の動向は現今の教科書や受験参考書には見られない珍しい話題と言えよう. 因みに, この書籍には巻末に「索引」が掲載されている. これも (先述した「學用語對譯」と同様に) 読者の便宜を図ってのことであるが, これを掲載することは, 当時の和製数学書としては初めてに近い試みであった. |
|||
| §4-7.『代数学講義』 | |||
| 前掲の教科書類は, その後の教育法の改正や時代の趨勢に則って種々の改訂版が出版された. 帝国大学教授として講義を続ける中で執筆されたのが, |
|||
| 『代數學講義』共立社, 1930, 全477頁 『初等整數論講義』共立社, 1931, 全496頁 『解析概論 微分積分法及初等関數論』岩波書店, 1938, 全600頁. |
|||
| であった. それぞれ, 貞治が, 55歳, 56歳, 63歳のときの著作である. これらの書籍は, 数学書としては異例のロングセラーであり, 今現在に至るまで頻繁に増刷され続けている. 特に『解析概論』は, (私は数学科出身ではないが, 数学科の友人たちの話では)「数学科の学生の必読書」と言われていたという. ただし, よく売れる書物がその読者達によって精読されているかとなると, 話は別である. 購入しただけで満足したり, 読み始めても途中で挫折したり, という声も少なくない. 私自身にとって,『初等整数論講義』は (本稿の冒頭でも述べたように)「フェルマーの最終定理」との関連性から学生時代に愛読した書籍であり, 他の二冊についても (これまで複数回に亘って) 読み返している. とは言え, 私がこれらの書籍を誤解なく真に理解しているかどうかは疑わしい.『ジャン・クリストフ』や『アンナ・カレーニナ』のような古典文学作品においても, 再読した際に, 初読の際の誤解に気づかされることがある. 内容が深ければ深いほど, 読み返すたびに新たな発見があるものである. 貞治の著作に関しても, 古典文学作品を再読するのと同等の感慨が得られることは事実である. このようなものを「名著」あるいは「古典」と言うのであろう. 以下, これらについても簡単に概略を記しておこう. 『代數學講義』は1948年に「改訂版」が出版され, その後, 貞治の没後 (1961年)に「改訂新版」が出版された. 以下, 引用の際は「改訂新版」から抜粋することにする. |
|||
 『代数学講義 改訂新版』(共立出版, 1965) |
|||
| 「序言」を見ると, |
|||
| 本書は著者がかつて東京大学で初級生のためにした一般向きの代数学講義に基づいて, それに多少の布桁を加えたものである. この講義の目的は, 僅少なる時間に於て,
迅速に代数学の基本概念を解説するにあった. 従って本書の目標とする所も, 代数学の大観であって, 系統的なる全書ではない. (中略) 成るべく多趣多様に代数的方法を紹介することを主眼とするのである. |
|||
| とある. 実際, この著作には一冊の数学書としては贅沢に過ぎるほどの豊富な題材が含まれていると言えよう. |
|||
| 第1章「複素数」では, その四則, 幾何学的表示, 一次有理関数, 等角写像が扱われる. これは, 次章以降で必要となる基礎事項である. 貞治は,
章末において複素数史を簡単に解説している. |
|||
| Gauss は1799年にその学士論文で代数学の基本定理の証明を発表した後, 整数論の問題に複素数を適用して偉大な成功をもたらし, 次いで
Cauchy は函数論を複素変数の上に築いて, 18世紀の微積分法にまつわった多くの疑問に光明を与え, Abel および Jacobi の楕円函数の発見を可能にする素地を作った.
また射影幾何学の発達は, 幾何学においても, 虚数的原素を導入することの避くべからざることを示した. (中略) 19世紀の中頃に至って, 虚数が一般数学界において承認された後に\(\,1,i\:\)を原素とする二次元の複素数の範囲を更に拡張して多次元の複素数を数学に導入することが問題となった. Hamilton の四元法 (quaternions) や, Grassmann の広延論 (Ausdehnungslehre) がその最初の試みで (後略) |
|||
| このように述べた後, 貞治は四則を保存する数の範囲は複素数の範囲を超越し得ないことを簡潔に説明している. 第2章「方程式論の基本定理」では, 多項式の四則と連続性, 代数学の基本定理と根の連続性, 有理関数が解説された後, エルミート-ビーラーの定理, ガウスの定理, ラゲルの定理が掲げられる. これらの定理は, 貞治自身が「美しい定理」と表現するものである (p.66). |
|||
| 定理2.9 (Hermite) 方程式\(\,f(z)\!=\!0\,\)の根の虚数部の符号が全部同一であるとき, 係数の実部と虚部とを分けて\(\,f(z)\!=\!U(z)\!+\!iV(z)\,\)とすれば, \(U(z)\!=\!0\,\)も\(\,V(z)\!=\!0\,\)も実根のみをもって, かつ\(\,U(z)\,\)の根と\(\,V(z)\,\)の根とは互いに隔離する. |
|||
| 定理2.11 (Gauss) \(f(z)\!=\!0\,\)の根の全部を含む凸多角形は\(\,f^{\prime}(z)\!=\!0\,\)の根の全部を含む. |
|||
| 定理2.12 (Laguerre) (1) 方程式\(\,f(x)\!=\!0\,\)のすべての根を含む円を\(\,C\,\)とし, \(\xi\,\)を\(\,C\,\)の外に取れば, \(P(\xi,x)\!=\!0\,\)の根はすべて円\(\,C\,\)の内にある. (2) \(\xi\,\)が円\(\,C\,\)の周上にあっても同様であるが, 特に\(\,f(x)\!=\!0\,\)の根がことごとく\(\,C\,\)の周上にあるとき, \(\xi\,\)も\(\,C\,\)の周上に取るならば, \(P(\xi,x)\!=\!0\,\)の根もことごとく\(\,C\,\)の周上にある. (3) この場合に, \(P(\xi,x)\!=\!0\,\)の根と\(\,\xi\,\)とは\(\,C\,\)の周上において\(\,f(x)\!=\!0\,\)の根を隔離する. |
|||
| 応用する場面が実用上少なくなったからであろうか, これらの定理が現今の代数学書で採り上げられることはほとんどない. その意味ではもはや数学史上の「骨董品」の部類と言えよう. しかし, この著作の魅力はこのような美術品が多数展示されている点にある. 定理のみならず, 著書全般に亘って随所に鏤められた「問題」も, 演習用 (実用的) というよりは寧ろ鑑賞用とでも言うべき, 味わい深いものが多い. |
|||
| 第3章「スツルムの定理」においては, 方程式の根の個数とその近似を計算する. 前者に関しては, フーリエ の定理, デカルトの符号律, (与えられた正定数より大なる根の個数に関する)
ラゲルの定理が採り上げられ, 後者に関しては, ボルツァーノの定理およびロルの定理から平均値の定理を導出した上で, 解析的手法によりニュートンの方法とホーナーの方法が扱われるのである.
第4章「多項式の整除」, 第5章「対称式, 置換」, 第6章「三次および四次方程式」の内容は, その多くが『新撰代數學』と重複する. ここでは, ラグランジュの分解式の由来が新規に追加されている (p.174-176). 第7章「不可能の証明」では,「有理区域」(と貞治が称するところの代数体) の解説から始まり, アーベルによる (ガロア理論によらない) 原始的な方法を踏襲して, 五次以上の方程式の代数的解法の非存在性が示される. 応用として, 角の三等分の不可能性および正\(\,n\,\)角形の作図可能性が採り上げられている. 第8章「行列式」および第9章「二次形式」は, 全体のおよそ3分の1の頁数を占めている. この書籍の中心部分と言えよう. 前者においては, 連立方程式の原始的解法を導入部とし, 行列式の性質やクラーメルの公式, ラプラス展開, 小行列式に関するシルベスターの定理などが紹介される. 後者においては, 行列式を応用した二次形式論が展開される. 標準化やシルベスターの慣性法則, エルミート形式などであり, この箇所においても『新撰代數學』との重複が数多く認められる. 第10章「終結式 スツルムの問題と二次形式」では, 二次形式論を応用して, 方程式\(\,f\!=\!0,g\!=\!0\,\)の終結式から\(\,f,g\,\)の最大公約数の次数を得る手法を導出し, それをシュトゥルムの問題に適用する. 後半部の解説はやや精密さに欠けるが, この章の内容はこの著作の集大成として大変に面白い. 余談ながら, 貞治の著書内における二項係数の表記の変遷について触れておく.『新撰代数学』(p.40) では |
|||
| \({}_n\mathrm{C}_{\mu}\!= \!\displaystyle{\frac{\prod(n)}{\prod{\!\!\:\mu}\prod(n\!-\!\mu)}}\,\) |
|||
| と表記され,『普通教育代数教科書』(p.405) では | |||
| \(\,{}_n\mathrm{C}_r\!=\!\displaystyle{\frac{|\!\underline{\:n}} {|\!\underline{\:r}\:|\!\underline{\:n\!-\!r}}}\,\) (ただし\(\,|\!\underline{\:\:\:}\,\)は階乗を表す) |
|||
| と表記されていた二項係数は, 最終的に『代数学講義』(p.40) において |
|||
| \(\,\displaystyle{\binom{n}{k}\!=\! \frac{n(n\!-\!1)(n\!-\!2)\cdots(n\!-\!k\!+\!1)}{k\!\:!}}\,\) |
|||
| のように書き換えられた. その理由は「\({}_m\mathrm{C}_k\,\)などとしるせば, 肝心の\(\,n\,\)や\(\,k\,\)が目立たない」というのである.
私はこの最後の表記を好む者であるが, 現今の教科書類は\(\,{}_n\mathrm{C}_k\,\)なる表記で統一されているため, 残念ながら学校現場では使えない. |
|||
| §4-8.『初等整数論講義』 | |||
| 『代数学講義』の「姉妹篇」として執筆されたのが『初等整數論講義』である. これも貞治の没後 (1971年) に改訂版 (第2版) が出版されている. 以下の引用は全て第2版による. |
|||
 『初等整数論講義 第2版』(共立出版, 1971) |
|||
| 「初等整数論」なる書名をもつ数学書は, これまでに多数出版されている. とは言え, 何をもって「初等」とするかは著者ごとに多種多様であり, 明確な定義は存在しない. 貞治自身は, 初等整数論と題する第1章に関して,「序言」において, |
|||
| 有理整数のみを考察の範囲として進行することが不適当であると思われる所に到達して, そこを一段落とした | |||
| と述べている.「序言」では, これに続けて, 第2章以下の内容に関する簡単な説明がある. | |||
| 第2章連分数論は (中略) 整数的近似法 (Diophantische Approximation) の一斑を紹介する. (後略) 第3章では連分数論の応用として二元二次不定方程式を論ずる. ニ元二次不定方程式の解法は十八世紀数学の精華で, 貴重なる古典と言わねばなるまい. (後略) 第4章及び第5章に於ては二次の数体を例に取って代数的整数論の端緒を述べて, イデヤル論の概念を紹介する. (後略) 別に附録の一章を置いて, 二次体論の高等なる部分にも論及し, 且つ二次体のイデヤルの類数の計算及び算術級数中の素数に関する Dirichlet の定理の函数論的証明法を概説する. |
|||
| 『代数学講義』が広範囲に亘る代数分野を概観するものであったのに対し,『初等整数論講義』はその一部である「代数的整数論」延いては「類体論」を目的とする方面に内容を限定するものであった. 本稿の冒頭に引用した黒田成勝の「序」においても,「著者の主なる意図は, 本書を通じて, 読者が代数的整数論に到達するための正統的な道を示すことにある」と明記されている. 貞治が若い時分から「数」が内包する構造に拘り, 数論に興味関心を抱いて主要な研究対象としてきたことは, これまで見てきたことから明白であろう.「序文」の後半において, 貞治は次のように述べる. |
|||
| 整数論の方法は繊細である, 小心である, その理想は玲瓏にして些の陰翳をも留めざる所にある. 代数学でも, 函数論でも, 叉は幾何学でも, 整数論的の試練を経て始めて精妙の境地に入るのである. Gauss が整数論を数学中の数学と観じたる理由がここにある. | |||
| ここに提示されたガウスの言葉は, 恐らく「数学は科学の女王, 算術は数学の女王」"Die Mathematik ist die Königin der Wissenschaften, und die Arithmetik ist die Königin der Mathematik" を指すものであろう. 生前のガウスと親交のあった地質学者ザルトリウス (Sartorius von Waltershausen, 1809-1876) がガウスの没後すぐに出版した評伝『記憶の中のガウス』 |
|||
| [Sartorius] "Gauss zum Gedächtniss" S. Hirzel, 1856, 全108頁. | |||
| の79頁に掲載された文言である.「算術」"Arithmetik" は, ガウスの『整数論研究』 | |||
| [Gauss D.A.] "Disquisitiones Arithmeticae" In commiss. apud Gerh. Fleischer, jun., 1801, 全668頁. | |||
 ガウス『整数論研究』(1801) |
|||
| に見られる通り,「整数論」と同義である. |
|||
| 第1章「初等整数論」は, 除法の原理, 素因数分解, 一次不定方程式と合同式, 原始根と指数, 平方剰余の相互法則など, 整数論の基本事項が次々と簡明に解説され,
読者を一気に惹き込む豊富な内容をもつ. 中でも章末にある円周等分多項式と1の冪根から正17角形の作図可能性に至る解説において, 結果の意外性と手法の鮮やかさは初学者を感嘆させるであろう. 第2章「連分数」では, 実数や複素数の連分数展開, 連分数による一次形式論 (ミンコフスキの定理), モジュラル変形による複素数の対等, 無理数の近似と格子点との美しい調和関係が開陳される. 学生時代の私は, 連分数論を応用して方程式の近似解を得る手法や, モジュラー群の基本領域がもつ神秘的な構造に特に魅了されたのであった. 第3章「二元二次不定方程式」では, 二次無理数の対等と連分数展開, 二次無理数の自己変形定理とペル方程式, 二次不定方程式の解法が解説される. 章末に現れる貞治の数学史観 (pp.239-240) は, 特に読者の興味を引くであろう. |
|||
| Gauss の「整数論」では克明に無理数を忌避して, 二次形式を専用しているけれども, それは一種の韜晦であって, 頭の中では\(\,\omega\,\)によって構成した理論を発表するのみ\(\,f\,\)を籍りたかの観がある.
特に\(\,\omega\,\)が虚数 (\(D\!<\!0\)) の場合に, このカムフラージュが最も周到であったのは, 当時の数学界の虚数に対する蒙昧な態度を考慮して,
Gauss のいわゆる頑迷者流の誤解を予防するに至当な戒心であったかと推察される. 「整数論」の後三十年を経て Gauss の複素整数論 (1832) が発表された. (後略) |
|||
| 上記における「整数論」および「複素整数論」とは, 上掲の [Gauss D.A.] および |
|||
| [Gauss1] "Theoria residuorum biquadraticorum, Commentatio secunda" Soc. Regiae Sci. Gött., 1832, pp.89-148. | |||
| である. [Gauss1] では, ガウスの整数環が提示され, 四次剰余の相互法則が (証明なしで) 紹介されている. ガウスの研究レヴェルが当時の数学界一般の理解度を遥かに凌駕していたことはよく知られていよう. 彼らの能力を考慮したガウスは, レヴェルを下げて敢えて迂遠なる方法で理論を組み立て直さなければならなかったのである. 貞治は, その当時の事情を次のように続けて記す. |
|||
| 現代の整数論は Fermat (1601-1665) 以来徐々に成育しつつあったのであるが, 十八世紀に至って, 特に Euler (1707-1783),
Lagrange (1736-1813) の努力によって, 二元二次の不定方程式の解法が成就する程度にまで発達して, 数学の一分科を構成するのに十分な域に達したのである.
Legendre (1752-1833) の「整数の理論の試作」(Essai sur la théorie des nombres, 1798) は十八世紀の終りにおける整数論の概括的展観であって, その書名が「整数論」という語の濫觴である. 当時の数学界から仰視されていたこの Essai は未だ平方剰余の相互法則を確定することもできず, また二次不定方程式を解き得ても, その理論が完成されてあるとはいい難い程度のものであった. |
|||
| ルジャンドル (Adrien-Marie Legendre, 1752-1833) の "Essai" すなわち |
|||
| [Lagrange] "Essai sur la théorie des nombres" Duprat, 1798, 全471頁. | |||
| の「序文」において, ルジャンドルは, 自身の業績として, 二次無理数と循環連分数の対等性, 四平方定理, 算術級数中の素数に関する定理の一般的方法,
の3つを挙げた. 彼は, この最後の業績を「最も注目すべきもの」"Le plus remarquable" と自負したのであったが,
実際にはその一部, すなわち『初等整数論講義』(p.56) にある「\(mt\!+\!1\,\)の形の素数は無限に存在する」を示したに過ぎなかった. 完全な証明がディリクレ (前出, §2-3.) によるものであったことは, 現在では周知の事実である. とは言え, フェルマーやオイラーの業績を初めとする整数論関連の諸結果を微に入り細に亘って解説している点に鑑みれば,「当時の数学界から仰視されていた」のも頷けるであろう. 特に, 巻末に掲げられた (二次形式, ペル方程式, 平方剰余関連の)「数表」は, 30頁以上にも及ぶ労作である! ところが, その労作 [Lagrange] の運命はその後どうなったか. 貞治は次のように述べて第3章を終える. |
|||
| そのような世界へ卒然として投げ出されたのが24歳の青年 Gauss (1777-1855) の Disquisitiones (1801)
である. その第四編において初めて相互法則の確定的の証明が提供され, かつその重大性が明示された. またその第五編, 二次形式論の前半において,
二次不定方程式の統一的の理論が構築されている. (中略) Disquisitiones の出現とともに, Essai は三年の寿命をもって急転直下, 数学史料に化してしまったのである. 数学史上の奇観といわねばならない. |
|||
| [Gauss D.A.] が出版された1801年当時, ガウスは24歳, ラグランジュは65歳の老大家であった. ラグランジュにしてみれば若輩者のガウスには苦々しい想いをさせられたことであろう. この辺りに端を発する二人の確執 (それは一方的にラグランジュ側の問題であったが) については, 後に『近世数学史談』に詳しく紹介されることになる. |
|||
| 第4章「二次体\(\,K(i),\,K(\sqrt{-3\,})\,\)の整数」では, ガウスの整数環, \(x^2\!+y^2\!=a\,\)の解が説明され,
応用としてフェルマーの問題 (\(n\!=\!4,3\)) が解決される. 第4章を敷衍した一般論が展開される第5章「二次体の整数論」は, この著作における中心主題である. 二次体とその整数環, イデアル論の基本定理までが解説される. その後, イデアルの類別, 既約類の個数や特定のイデアルを法とするフェルマーの定理などが示され, ペル方程式や二元二次方程式に応用される. 定理5.18「二次体の素イデアルは三種に分かれる」(pp.292-294) や「与えられたノルムを有するイデアル」(pp.325-326) は, 二次体のイデアルにおける肝要部分である. ここには複数の例や問題が付されており, 貞治の読者に対する細かな配慮が読者の理解度を大いに高める役割を担っていると言えよう. 第5章の内容は『代数的整数論』前半部にある諸事項を二次体に適用したものであり, 両書を対比して読めば, 双方の理解を助けることになるであろう. 余談であるが, (『髙等敎育代數學』に現れたような) 数を表す文字に関する貞治の思想は, ここでも顔を出す. p.277の脚注を見ると, |
|||
| イデアルを表わすにはドイツ文字を用いるのが慣例であるが, 本書では便宜上イタリックの大文字を代表する. 筆者はイデヤル論を世界的に普及せしめるために, ドイツ文字専用の慣例をやめて欲しいと思う. ただし二次体論はこれでよいが, 高等整数論ではさしつかえが生ずるから別の考慮を要する. | |||
| と記されている. 最後の一文は1931年の初版 (p.327) には見られないから, 1933年に岩波数学講座『代数的整数論』を執筆した際に気づいた点を, その後の増刷版において付加したものと思われる. ところで,『初等整数論講義』の巻末に付された「附録」は, 第5章に匹敵する注目すべき項目である. 代数的整数論への階梯として, まずイデアルの類別について広義と狭義が区別され, ノルム剰余およびイデアルの属する種に関して解説される. 続いて, 平方剰余の相互法則が二次体のイデアル論を用いて証明される. その単純明快ぶりは読者を感嘆させるであろう. |
|||
| さらに, イデアル類の類数と算術級数中の素数の定理の証明 (ディリクレの業績) の要点が解説される. 前者は, \(K(\sqrt{m\,})\,\)のイデアル\(\,J\,\)によるデデキントのゼータ関数 |
|||
| \(\displaystyle{\zeta_{{}_{K}}\!\:(s)= \sum_{}^{J}\frac{1}{\!\:\mathrm{N}(J)^{{}^{s}}\!\:}}\) |
|||
| を, \(K(\sqrt{m\,})\,\)における素イデアル\(\,P\,\)を用いて | |||
| \(\displaystyle{\zeta_{{}_{K}}\!\:(s)= \prod_{}^{P}\frac{1}{\!\:1\!-\!\mathrm{N}(P)^{{}^{-\!\:s}}\!\:}}\) |
|||
| のように無限乗積展開したものを, 素イデアル三種を指標\(\,\chi(p)\,\)(p.295) で置き換えて | |||
| \(\displaystyle{L_{\!\!\:{}_{K}}\!\:(s)= \prod_{}^{p}\frac{1}{\!\:1\!-\!\chi(p)\,p^{{}^{-\!\:s}}\!\:}= \sum_{n\!\:=\!\:1}^{\infty}\!\frac{\!\:\chi(n)}{n^s}}\) |
|||
| なる別表記にした上で, 極限\(\,s\!\to\!1\,\)をとり, 狭義のイデアル類数\(\,h_{\kappa}\,\)を無限級数の和\(\,\displaystyle{\sum_{n\!\:=\!\:1}^{\infty}\!\frac{\!\:\chi(n)\!\:}{n}}\,\)として求めるものである. 後者は, \(\mathrm{mod}.\!\!\:k\,\)に関する指標\(\,\chi(n)\,\)による\(L\,\)関数 |
|||
| \(\displaystyle{L\!\:(s,\chi)=\sum_{n\!\:=\!\:1}^{\infty}\!\frac{\!\:\chi(n)\!\:}{n^s} =\prod_{}^{p}\frac{1}{\!\:1\!-\!\chi(p)\,p^{{}^{-\!\:s}}\!\:}\:\:(s\!>\!1)}\) |
|||
| を三種の素イデアル (p.292) ごとに\(\,L_{1},L_{2},L_{3}\,\)とおいて | |||
| \(\displaystyle{\lim_{s\!\:\to1}\,(s\!-\!1)L_1(s)=\frac{\!\:\varphi(k)}{k},\: \lim L_2(s)\!=\!L_2(1)\,(\not=\!0),\:\:\lim L_3(s)\!=\!L_3(1)\,(\not=\!0)}\) |
|||
| を示した後, 全ての\(\,\chi\,\)に関する\(\,\log L\!\:(s,\chi)\,\)の和 | |||
| \(\displaystyle{\sum^{\chi}\log L\!\:(s,\chi)= \varphi(k){\sum}^{\,\prime}\!\frac{1}{\!\:p^s}\!+\!S\:\:(s\!\geq\!1}\,\)のとき\(\,|S|\!<\!\varphi(k),\:\:p\!\equiv\!1\:(\mathrm{mod}.\!\!\:k))\) |
|||
| を考え, 極限\(\,s\!\to\!1\,\)をとった上で\(\,p\!\equiv\!m\,(\mathrm{mod}.\!\!\:k)\,\)なる有理素数\(\,p\,\)の存在を示すというものである. 何れも厳密に理解することは容易ではないが, 貞治による解説は極めて平易であり, 読者を納得させるものになっている. 最後に, 上述の証明に用いられたガウスの和 |
|||
| \(\displaystyle{\sum^{r}\chi(r)\,\mathrm{exp}\left(\frac{2\pi i}{|\!\:d\!\:|\!\:}nr\right) =\chi(n)\sqrt{\!d\,}}\) |
|||
| の証明が与えられる. これは,「Gauss が数年苦心の後ようやく解決することを得たといっている」(p.392) 方法であり, 甚だ技巧的であるが,
貞治の述べる通り「含蓄の多い」ものである. その末尾において, 貞治は |
|||
| 二次体と1の巾根との間に密接な関係のあることが感ぜられるであろう. 有理整数に関する二次の問題が二次体の問題として取り扱われるときに透明なる解釈が可能で
(中略) 二次体の整数論もさらに一段の高所から見おろすときに, 初めてその全景をほしいままに展望することができるのである. その展望台は, すなわち1の巾根から生ずる数体
(Abel 体) の理論 (現代的の「円理」!) である. われわれは明媚なる風景に魅惑せられて, いつか予定の目標を超えて, 思わず深入りをしたが, このあたりでひとまず馬を返さねばなるまい. |
|||
| という, 読者を代数的整数論への入口へ導く文言を文学的な味のある表現で全体を締め括っている. 内容の明快さや深さも然ることながら, 随所に見られる貞治独特の文学的な表現は,『初等整数論講義』を「名著」たらしめている根幹の一つと言ってよい. 高校時代に小説家を志して文科系のクラスに属していた私が, 勤務校の生徒達に向けて『初等整数論講義』をたびたび紹介してきたのは, 本書によって私自身が数学に惹き込まれたことのみならず, そこに文学作品を読むような味わい深さを感じてきたからにほかならない. |
|||
| §4-9.『解析概論』 | |||
| [百年史上] (p.253) によれば, 藤澤利喜太郎が定年退官した翌年の1922年当時, 東京帝大数学科における必修科目の講座を受け持っていたのは, |
|||
| ・第一講座 [関数論] 竹内端三 ・第二講座 [微分積分学] 坂井英太郎 ・第三講座 [代数学] 高木貞治 ・第四講座 [微分方程式論] 吉江琢兒 ・応用数学講座 [幾何学] 中川銓吉 |
|||
| であった. 貞治は20年以上もの間, 一貫して代数学を講じていたわけである. 学生時代より藤澤利喜太郎に代数学の必要性を吹き込まれ, アーベル方程式を勧められて類体論まで創設した貞治は, 自他ともに認める代数学の専門家であり, 当然これは貞治が担当すべき講座であった. ところが, [百年史下] (pp.4-5) によれば, |
|||
| 昭和時代に入ると学生や大学院生の数もふえ, とくに高木, 吉江の指導の指導の下に若い層の研究は一段と活気を呈することになる. (中略) 講義の担当者は, 微分積分学は坂井から1932年に高木に移り, (中略) 代数学の講義は1932年に高木から末綱に移った. |
|||
| という (pp.4-5). 末綱恕一 (1898-1970) は, 正田建次郎 (1902-1977), 菅原正夫 (1902-1970), 黒田成勝 (前出, §1-1.), 三村征雄 (1904-1984), 彌永昌吉 (前出, §3-5.) などの「貞治から直接指導を受けた数学者」のうちの最初期の人物であり, 1924年から東京帝大の助教授に就任していた. 帝国大学令が公布された1919年以降「必修, 選択, 参考科目の区別が付けられ, 卒業の要件として, 必修科目の履修の他に, 選択科目を2科目以上修得しなければならないこととなった」という. 末綱は, 選択科目「解析的整数論」も担当していたようである ([百年史上] p.231, p.253). 代数学の大家であったとは言え, 貞治による類体論は (先述したように) ゼータ関数や\(\,L\,\)関数など解析関係の道具を駆使している. これが可能であったのは, 貞治自身が若い時分に専門分野を早急に狭めてしまわず, 縦横無尽に種々の分野の数学を咀嚼吸収してきたからこそであった. 貞治が担当した「微分積分学」について, 彌永昌吉は |
|||
| [彌永9] 『河田君のこと』/『柔らかい頭と強い腕 河田敬義追想集』私家版, 1994, pp.13-14. | |||
| において | |||
| 1935年の4月に始まった学年では, 高木先生は, 前期の微分積分学の講義を受け持たれた. 微分積分学というのが, 当時の学科の名前であったが, 内容は先生の『解析概論』と大体同じであった. (先生は, 長い間代数学や整数論の講義をしておられたが, 坂井英太郎先生が定年退職された1932年から前期の微分積分学を受け持たれた. それを岩波講座に書かれたのがもとになって『解析概論』ができたのである. もっとも最後のルベーグ積分の章だけは, 増訂版で追加された). | |||
| と述べている. この講義に関しては, 後年, 多くの学者達によってその印象が語られることになる (詳細は最終節 (§6.) で紹介する). 僅か半年間の講義で, しかも与えられた時間よりも短時間で講義を済ませてしまったようであるが, 過不足のない充実した講義であったという. |
|||
| 実際,『解析概論』は, 貞治自身が監修した岩波講座 "数学" 全30巻 (1932-1935) の中の8分冊分を, 後に単行本化したものである
([百年史下] p.137). 1932年から1935年に亘って刊行された岩波講座には, 貞治のほか, 小松醇郎 (1909-1993), 藤原松三郎 (1881-1946), 窪田忠彦 (1885-1952) 達が編集委員に加わっていたようである. 森茂雄『書物は手元に』(前出書 [追想高木] p.68) には, |
|||
| 偶々グルサの Cours d'analyse の全訳の原稿を岩波書店の編集部に持ち込んだ人がいて, その上梓の是非について先生方のご意見を伺ってくれと頼まれていましたので, その趣きを席上で披露しました. そのとき, 先生は,「最早, 我々の手で適切な解析の書物を作り上げる時に来ているのではないか」という意味のことを述べられ, 同席していた岩波茂雄氏から,「先生が, この気概をお持ちなのに, お若い方が学ばなければ」と批判されたこともありました. | |||
| とある. 編集会議でこのように述べた貞治は,『解析概論』を自ら執筆したのであった. 「微分積分法及初等関數論」なる副題が付された初版以降, ルベーグ積分を含めた増訂版 (1943), 改訂第三版 (1961年), 改訂第三版 [軽装版] (1983) を経て, 現在刊行されているものは [定本] 版 (2010) である. 私が学生時代に所蔵していたのは [軽装版] であるが, 以下の引用は全て, 現在の私が所蔵している [改訂第三版] (1961) からの抜粋である. |
|||
 『解析概論 改訂第三版』(岩波書店, 1983) |
 『定本 解析概論』(岩波書店, 2010) |
||
| これは,『初等整数論講義』に匹敵する名著と言えよう. 標題において「講義」とは銘打ってはいないものの, やはり文体は講義式であり, その意味では他の専門書に比して表現はやや冗長ではあるが, 講義の流れは自然であり, 内容に関しては一切の無駄がなく興味深いものばかりである. 「第一版 緒言」には, |
|||
| 本書は, 著者の意図においては, 時代に順応した一般向きの解析学予修書, あるいはむしろ解析学読本で, なるべく少量の一冊子内において, 解析学の基本事項を大観して, 自由に各特殊部門に入るべき素養を与えることを目標とするものである. (中略) 予修書としての解析概論は繁冗を厭うて簡明を尊ぶことはもちろんであるが, 本書が著者の予想を裏切って意外に部厚になった一つの原因は講義式の叙述にある. 数学の解説法において, (中略) 一つをかりに教本式というならば, Euclid の幾何学原本がその典型とされ (中略) 既成の理論を整理して, それを論理的の系統に従って展開する方法で, その特色は正確と簡潔と, そうして難読とにある. (中略) 行と行との中間の空白を読むことを要するであろう (中略) 講義式は (中略) 数学上の概念発生の源をたずね, 理論進展の跡を追う方法で (中略) 数学を活き物として, その生長の一つのフェイズを捕らえようとするところに若干の新鮮味があり得るであろう. |
|||
| と述べてある. 展示化石のような無味乾燥な数学ではなく,『初等整数論講義』と同様, 貞治自身の裡から湧き出てくる活きた数学を味わえるのである. 目次からその内容を概観すると, |
|||
| 第1章 基本的な概念 (実数の連続性, 数列の極限, コーシーの判定法, 連続函数の性質) 第2章 微分法 (種々の微分, 偏微分, 全微分, 極大極小, 接線, 曲率) 第3章 積分法 (求積法, 定積分, 原始関数, 広義積分, 種々の積分, ルジャンドルの球函数, 不定積分, 曲線の長さ, 線積分) 第4章 無限級数 一様収束 (種々の収束, 収束判定, 二重級数, 無限積, 巾級数, 種々の函数) 第5章 解析函数 特に初等函数 (コーシーの積分定理, 積分公式, 解析函数のテイラー展開, 解析接続, 有理函数の積分論, ガンマ函数, スターリングの公式) 第6章 フーリエ式展開 (フーリエ級数, 函数系の直交化, 相加平均総和法 (フェイエールの定理), 連続函数に関するヴァイエルシュトラスの定理, 積分における第ニ平均値定理, フーリエ級数に関するディリクレ-ジョルダンの条件, フーリエの積分公式) 第7章 微分法の続き (陰伏函数, 曲線の方程式, 曲面の方程式, 包絡線, 陰伏函数の極値) 第8章 多変数の積分法 (二次元以上の定積分, 多変数の定積分によって表される函数, 曲面積, 曲線座標, 面積分, ガウスの定理, ストークスの定理, 完全微分の条件) 第9章 ルベーク積分 (加法的集合族, ルベーグ測度論, ボレル集合, 累次積分, リーマン積分との比較, スティルチェス積分, ヴィタリの被覆定理, 加法的集合函数の微分法, 有界変動・絶対連続の点函数) 附録 (I) 無理数論 (有理数の切断, 実数の連続性, 極限, 巾根, 複素数) 附録 (II) ニ, 三の特異な曲線 |
|||
| となる. |
|||
| 他書にはあまり類を見ないが,『解析概論』には, 目次の直後に「定理索引」なるものが付されている. 残念ながら定理番号とページ番号のみの記載であるため, 内容までは直ちには判断できない. 次に示すように, 内容を明記した索引であれば, より読者への便宜となるであろう.
試みに, 第1章に現れる定理を全て挙げてみよう. |
|||
| 定理1. 実数の切断は, 下組と上組との境界として, 一つの数を確定する [Dedekind の定理]. |
|||
| 定理2. 数の集合\(\,S\,\)が上方 [または下方] に有界ならば\(\,S\,\)の上限 [または下限] が存在する [Weierstrass の定理]. | |||
| 定理3. 収束数列の部分数列は, もとの極限値に収束する. |
|||
| 定理4. \(a_n\!\to\!\alpha\,\)ならば, \(|a_n|\!<\!M\,\)なる定数\(\,M\,\)がある. そうして\(\,|\!\:\alpha\!\:|\!\geq\!M\). |
|||
| 定理5. \(\{a_n\},\{b_n\}\,\)が収束するとき, | |||
| (1) \(\displaystyle{\lim_{n\to\infty}(a_n\!+\!b_n) =\lim_{n\to\infty}a_n\!+\!\lim_{n\to\infty}b_n}\). (2) \(\displaystyle{\lim_{n\to\infty}(a_n\!-\!b_n)= \lim_{n\to\infty}a_n\!-\!\lim_{n\to\infty}b_n}\). (3) \(\displaystyle{\lim_{n\to\infty}(a_n b_n)= (\lim_{n\to\infty}a_n)(\lim_{n\to\infty}b_n)}\). (4) \(\displaystyle{\lim_{n\to\infty}(a_n/b_n)= (\lim_{n\to\infty}a_n)/(\lim_{n\to\infty}b_n)}\). |
|||
| 定理6. 有界なる単調数列は収束する. | |||
| 定理7. 閉区間\(\,I_n\!=\![\!\:a_n,b_n]\:(n\!=\!1,2,\cdots)\,\)において, 各区間\(\,I_n\,\)がその前の区間\(\,I_{n-1}\,\)に含まれ,
\(n\,\)が限りなく増すとき, 区間\(\,I_n\,\)の幅\(\,b_n\!-\!a_n\,\)が限りなく小さくなるとすれば, これらの各区間に共通なるただ一つの点が存在する. |
|||
| 定理8. 数列\(\,\{a_n\}\,\)が収束するための必要かつ十分なる条件は, 任意の\(\,\varepsilon\!>\!0\,\)に対応して番号\(\,n_{{}_{0}}\,\)が定められて, | |||
| \(p\!>\!n_{{}_{0}},\:q\!>\!n_{{}_{0}}\) なるとき \(|\!\:a_p\!-\!a_q\!\:|\!<\!\varepsilon\) | |||
| なることである. | |||
| 定理9. 有界なる無数の点の集合に関して, 集積点が必ず存在する [Weierstrass の定理]. | |||
| 定理10. 有界なる閉集合の列\(\,S_1,S_2,\cdots\,\)において, | |||
| (1) \(S_1\!\supset\!S_2\!\supset\!\cdots\!\supset\!S_n\!\supset\!\cdots\) (2) \(n\,\)が限りなく増大するとき, \(S_n\,\)の径が限りなく小さくなる |
|||
| ならば, これらの集合\(\,S_n\,\)に共通なる点がただ一つ存在する. | |||
| 定理11. 無数の円の一組が, 全体として, 有界なる閉集合\(\,F\,\)を覆うならば, \(F\,\)はすでに, それらの円の中の有限個だけで覆われる [Heine-Borel の被覆定理]. | |||
| 定理12. 或る区間において連続なる函数\(\,f(x)\,\)が, この区間に属する点\(\,a,b\,\)において相異なる値\(\,f(a)\!=\!\alpha,\,f(b)\!=\!\beta\,\)を有するとき, \(\alpha,\beta\,\)の中間にある任意の値を\(\,\mu\,\)とすれば, \(f(x)\,\)は\(\,a,b\,\)の中間の或る点\(\,c\,\)において, この\(\,\mu\,\)なる値を取る. すなわち | |||
| \(a\!<\!c\!<\!b,\:f(c)\!=\!\mu\) | |||
| なる\(\,c\,\)が存在する [中間値の定理]. | |||
| 定理13. 有界なる閉区域\(\,K\,\)において連続なる函数\(\,f(P)\,\)は有界で, かつその区域において最大および最小の値に到達する. | |||
| 定理14. 有界なる閉区域\(\,K\,\)において, \(f(P)\,\)は連続とする. 正なる\(\,\varepsilon\,\)が任意に与えられたとき, それに対応して正なる\(\,\delta\,\)があって, 区域\(\,K\,\)の任意の点\(\,P,Q\,\)に関して | |||
| \(PQ\!<\!\delta\) なるとき \(|\!\:f(P)\!-\!f(Q)\!\:|\!<\!\varepsilon\) | |||
| になる [連続の一様性]. | |||
| 第1章で提示されるのは, 以上の14定理である. |
|||
| 学生時代の私は, 内容を明記した (上掲のような)「定理索引」を, 数学書を繙くたびに作成していた. 一般に, 数学書 (演習書や解説書や啓蒙書などを除く) は一読して理解できるものではない. 従って, 初読の際は細部に拘泥せず全体を通読し, その際に,「定義索引」および上記のような「定理索引」をノートに作成する. その書籍における概要はこれで把握できる. 二回目は少し念入りに細部まで読む (定理における証明も丁寧に書き写す). それでも理解できない箇所は少なくない. これを, 三回目以降は精読をもって更に丹念に読む (章末の練習問題を全て解く時間的余裕はないが, 定理に該当するものは書き写す). これを繰り返すうち, 徐々に細部まで理解できるようになる. ―― 私自身が数学書を繙く際に適用してきた読書法はこれである. 最初から精読して全てを理解しようとすると大抵は挫折する. 適当な間隔をおいて幾度か丁寧に読み返すことが, 数学書を理解するには最も有効であろう. 巷間には, 再読する気になれない (無味乾燥な) 数学書も存在するが, 貞治の著書の場合は,「読み返すたびに新たな発見があ」ると先に述べた通りである. ところで, 上掲の定理は全て, 大学初年度で必ず修得すべき基礎事項である. これらを導く貞治による叙述は全般に亘って簡単明瞭であり, 疑問を挟む余地は全くない. とは言え, 貞治の叙述が明快であることと読者がその内容を明晰に理解することとは, 全く別の話である. より高度の厳密性を追求する読者ならば, 貞治の解説をさらにキメ細かなものにすべく, 上記の各定理の間に補助定理 (補題) を設けるであろう. 定理以外の箇所についても同様である. 例えば第1章の冒頭部において, 貞治は, \(n\,\)次元ユークリッド空間の点\(\,P,P^{\prime\!},P^{\prime\prime}\,\)について, 三角不等式\(\,PP^{\prime}\!+\!P^{\prime}\!P^{\prime\prime}\!\geq\!PP^{\prime\prime}\,\)を (根拠を示すことなく) 掲げている. 貞治の記載方法はあくまでも明快である. 大学初級生でも何の疑問もたずに読み進めるに違いない. \(\mathbb{R}^2\,\)や\(\,\mathbb{R}^3\,\)における直観的に明白な三角不等式は (高校生でも) 知っているからである. しかし, \(\mathbb{R}^n\,\)における三角不等式が成り立つ理由を問われた場合, 初学者の大半は説明に躓くであろう. 「明晰に理解する」とは,「与えられた定義が well-defined か, 与えられた条件ないし仮定は必要十分か, などを吟味し, これを根拠として, 記載事項ないし命題の真なる理由を一つ残らず論理的に説明できる」ことを意味する. 貞治が「緒言」に記した「行と行との中間の空白を読むことを要する」なる姿勢は, 教本式のみならず講義式で書かれた書籍に対しても必要であり, 後年に教え子達も述べているように (最終節参照), これは, 貞治が学生に対してたびたび注意を促したことでもあった. 『解析概論』は, 出版直後から現在に至るまで (恐らく最も) 人口に膾炙した数学書であるが, その読みやすさに比して, 真に理解することは容易ではないと言えよう. 無論, これは『解析概論』に限ったことではないのであるが……. |
|||
| 先に引用した「第一版 緒言」には続きがある. | |||
| 解析概論に取入れるべき材料の取捨が他の一つの困難な問題である. (中略) 一例として指数函数, 三角函数を取ってみる. (中略) その古典的導入法は, 全く歴史的, 従って偶発的で, すこぶる非論理的と言わねばなるまい. さて解析概論において, その歴史的発生を無視することが許されないとするならば, これらの函数の合理的導入法を述べる上に, 古典的導入法が偶発的である所以をも説くことが, 解析概論に課せられる迷惑な任務というものであろう. (中略) 本書が理想的の薄さに止め得なかった他の原因がここにある. 基礎的の事項に関してはなるべく論証の明確を努めて, 応用的の部門においては解法の敏活を主として, 微細な論点を読者の補充に委任した. 各章の終りに少数の練習問題を配置して, 読者の任意使用に供したが, 精選を期したのではない. 解法の示唆を附記して置いたけれども, 誤算の有無は保証されないのだから, もとより拘泥すべきではない. (後略) |
|||
| 『解析概論』を執筆した当人しか体験し得ない苦心談がここに吐露されている. それまでの解析学書における表記法や証明法に創意工夫に満ちた改良を施し, 過不足のない洗練された内容と生の講義を髣髴とさせるような格調の高さにより, 出版後87年もの期間 (2025年時点で) に亘って読み継がれ, 多くの数学徒を感化してきた数学書である. しかし, 進化発展し続ける長い数学史の中では, その内容や視点に関して次第に経年劣化していく面が生ずることは已むを得まい. 直接的に貞治に教えを受けていない者達 (数学者を含む) から見れば, 貞治は数学史上において既に伝説化 (神格化) された存在である. それに対する感覚的な「憧憬」や「反発」を抱く者が多いことは頷ける. 「憧憬」ならば問題はない. 数学的に向上途中にある数学徒にとって前向きな動機となり得るからである. 障害となるのは「反発」の方である. これは多くの真面目な数学徒を困惑させ誤解させる可能性があり, 実害が生ずる. 実際, 後の時代の (貞治に師事していない) 数学者達による『解析概論』に対する批判は少なくない. 例えば, 微分方程式の章が存在しないのは (物理への応用が利かず) 片手落ちである, あるいは, 増訂版における (木に竹を接ぐような, または, 講義式ではなく教本式に書かれた) ルベーグ積分の後づけは初版が有していた全体の統一性を崩した, などという構成法に関する批判がある. また, 方法論に関する批判, 例えば実数の連続性 (p.3) や弧長を含む不等式 (p.21) における条件不備を初めとする, 各所に対する記述の改正を要求するものもある. 貞治がこれらの批判を考慮しなかったわけではあるまい. それでもなお, 一般の数学徒に対して「解析学の基本事項を大観して, 自由に各特殊部門に入るべき素養を与えること」を敢えて優先させ,「微細な論点を読者の補充に委任し」て『解析概論』を纏めたのである. そこに, 貞治が苦心談を書かざるを得なかった所以がある. 余談であるが, SNS上では, 自身の数学力を過信した者達 (多くは数学科出身者か?) による誹謗中傷も少なからず目につく. 彼らの皮相的感情的な物言いから判断して, (上記に述べたような) 一部の数学者達による批判を鵜呑みにして便乗したに過ぎず, 彼ら自体は,『解析概論』を自身の力では読めていない (内容を理解してはいない). 上記の苦心談の吐露を含め, 貞治が随所に見せた (本稿でもたびたび指摘してきた)「数学に対する謙虚な姿勢」を, 彼等にも見習って頂きたいと思う. 畢竟,『解析概論』を真に批判できる者は, これを凌駕する解析学書を書いた者以外にはないのであろう. そして, そのような偉業を成し得た者は, 今現在に至るまで一人も存在していない. これまでに出版された夥しい数の解析学書の中でも, 例えば, 一松信『解析学序説 上・下』(裳華房, 1962-1963) や, 赤摂也『微分学+積分学』(数学セミナーリーディングス, 日本評論社, 1973) などは, 随所に工夫が施されている名著であるとは思うが, とは言え, (あくまでも私の主観であるが)『解析概論』を凌駕しているとまでは言えない. ……斯く言う私自身は, (言うまでもなく) 貞治に対する感覚的な「憧憬」の念を抱く輩の一味である. |
|||
| 『解析概論』における講義式の流暢かつ平易な論理の流れは, この書を大変に魅力的なものにしている. さらに,『代数学講義』や『初等整数論講義』と同様, 各種多方面の趣向を網羅するような重要かつ典型的な例題 (章末問題を含む) が充実している点も大変に魅力的と言えよう. それらは, 修学のための演習問題であることは無論であるが, 寧ろ, 時間を掛けて鑑賞すべき美術品と言ってよいものである. 『解析概論』が魅力的な書物であるもう一つの大きな理由は, これも他の著書と同様, 貞治の数学思想が随所に垣間見えることである. 以下, 少し抜粋してみよう. |
|||
| 内点, 外点, 境界点は直感的ないい表わしであるが, それらの定義を (中略) すなおに受け入れて, 論理的に考えるならば, (中略) '非常識' な場合も容易に承認されるであろう. このような論理的の態度が解析学の理解に絶対的に必要であって, それがなくては, 応用が不安心であろう. (p.29) | |||
| 曲線とは何をいうか. (中略) 便宜上幾何学的の用語を使うけれども, 空間的の直観を論理の根拠とはしないつもりだ (後略). (p.32) | |||
| 面積を使って, むぞうさに原始函数を出してしまったが, 原始函数の存在が問題になるならば, 面積の可能性も同様でなければならない. 我々は無頓着に面積, 体積などといっているが, そもそも面積, 体積とは何を意味するか? (p.90). | |||
| §8, [例7] の函数は (中略) 任意の小区間内に不連続点が (無数に) ある. それでも積分可能!(p.96) | |||
| 微分積分法の基本公式は (中略) 連続函数に関する限り, 微分と積分とが互に逆な算法であることを意味する. もしも連続性を仮定しないならば, この関係は成立しない. (中略) 連続函数以外では, 微分積分法はむずかしい!(pp.101-102) | |||
| 各所に挟まれる貞治の私見や感想は, 読者側に積極的な問題意識を誘発させるであろう. このような文言に啓発されて, 読者は自発的な関心をもって先を読み進めることになるのである. |
|||
| 連続性を仮定しないで, 積分可能の条件を確定したのは Riemann (1854) であろう. (中略) Riemann 積分法からの, これより以上の収穫は, \(f(x)\,\)が有界ならば, 無数の不連続点があっても積分可能でありうるということの認識であるが, Riemann 積分法は積分論を終結させるのではない. 20世紀に入って, Lebesgue 積分論が出現してからは, Riemann 積分は中間的の存在になってしまった. ここでは, しばらく伝統に従って, Riemann 積分論を比較的に重く取り扱ったのである. (pp.109-110) |
|||
| ここに述べられていることは, 先述した [Gauss1] と [Lagrange] のような関係とは異なる. ルベーグ積分の出現によりリーマン積分の立場が「急転直下」したわけではない. (第ニ) 余弦定理の存在とは独立に三平方の定理が有用であるのと同様である. 貞治は「中間的の存在」と表現しているが, そこまで曖昧模糊とした立場に貶められてはいまい. これに関して貞治は, 増訂第二版における「序文」において |
|||
| Lebesgue 積分論は, 組立てにおいては, Saks に従い, 細目に関しては, Lebesgue の原著のほか, de la Vallée Poussin, Carathéodory, Hahn, Kilmogoroff 等を参考にして書いたが, (中略) Lebesgue 積分論の追加に伴って, 109頁に述べたような意味における Riemann 積分論の縮小は当然考えられるべきであったが, 伝統を顧慮してしばらく原形を存することにした. | |||
| と記している. 無論, 執筆当時における事情を述べたものであるから, 現代の視点から『解析概論』の構成法を批判されることは, 著者貞治にとっては心外というものであろう. |
|||
| 続きを見てみよう. |
|||
| 条件収束の級数は, 項の順序を適当に変更して, 任意の和に収束せしめ, または収束性を失わしめうることを, Dirichlet (1829) が指摘した. (中略) 収束性を度外において, 無限級数を有限級数のように放漫に取扱って, しばしば不可解の矛盾に逢着したことは, 18世紀数学の苦い経験であったのである. (p.146) |
|||
| 初等数学では, 指数函数\(\,a^x\,\)は任意指数\(\,x\,\)に関する巾として定義せられ, その逆函数として対数\(\,\mathrm{log}_ax\,\)が導かれる. 特に\(\,e^x\,\)の底\(\,e\,\)は\(\,\displaystyle{\lim_{n\to\infty}\!\left(\!1\!+\!\frac{1}{\!\:n\!\:}\!\right)^{\!\!\!\:n}}\,\)として定義された. これは指数函数の歴史的の発生で, その理論はかなり複雑といわねばならない. (p.189) | |||
| 今かりに微積分法の発見以前に, 三角函数が知られていなかったと想像するならば, 円弧の計算の必要上, 自然に積分\(\,\displaystyle{\theta\!=\!\!\int_{0}^{x}\!\!\frac{dx}{\!\sqrt{1\!-\!x^2\!\:}}}\,\)に遭遇したであろう. 青年 Gauss (1797) はレムニスケートの弧長に基づいて (中略)\(\,\displaystyle{\int_{}^{}\!\!\frac{dx}{\!\sqrt{1\!-\!x^2\!\:}}}\,\)を考察して, 楕円函数発見の糸口を得たのである. (p.193) | |||
| 実変数に関する三角函数, 双曲線函数は複素変数に関する指数函数の一断面にほかならないから, それらの逆函数がすべて対数函数に包括されるのである. この認識は大切である. (p.198) | |||
| これらの記述は, 現今の数学で用いている用語や定理が解析学史においてどのように発生発展してきたかを知る契機となるものであり, 読んでいて大変に面白い. 他の解析学書においてこのような記述を見る機会は稀である. 第5章「解析函数」は『解析概論』の中で最も充実した (高密度の) 解説が展開されていると言えよう. その流暢な論理性の素晴らしさは言うまでもないが, 随所に現れる貞治自身の解析函数に対する讃辞が読者の心を揺り動かすのである. 一般数学者にとってはこれらの諸理論は既に当然のこととして理解されるものであろうが, 貞治は初学の数学徒の知的好奇心を刺戟すべく自ら新鮮な感覚をもって解析函数の萌芽と成育状況を叙述したのである. 恐らく, 実際の講義でも同様の表現をもって学生達を刺戟したことであろう. |
|||
| 変数を複素数にまで拡張すること (中略) それによって古来專ら取扱われていたいわゆる初等函数の本性が初めて明らかになって, 微分積分法に魂が入ったのである. (p.201) | |||
| 微分可能といえば, 一語簡単であるが, 含蓄は多大である. だから有理函数や巾級数やに関しても, その '解析性' を伏せておいては, 真相がわかるものではあるまい!(p.204) | |||
| 実変数の函数においては, 微分がとかくめんどうで, 積分は一般に簡単であった. (中略) 解析函数の世界では, 正則性は微分しても積分しても動揺しない. そこに解析函数の実用性がある. (中略) 複素数の世界では, 微分可能も積分可能も同意語である. 驚嘆すべき朗らかさ! Cahchy およびそれに先だって Gauss が虚数積分に触れてから約百年を経て, 我々はこの玲瓏なる境地に達しえたのである. (p.216) | |||
| この引用部に記されたコーシーの定理の応用として, ディリクレ積分 (p.223) やフレネル積分 (p.224) が例として掲げられる. |
|||
| 或る一点の近傍において与えられた解析函数は, それの解析的延長が可能なる全領域において一定であるから, 拡張の及ぶ限り一定の法則によって支配される (中略). 18世紀には (中略) 各函数は天賦の法則に支配されるものと信ぜられた. それを Euler 式の連続性という. (中略) 無意識的に夢想されていた法則上の連続性が解析函数によって, 最初の一例として, 実現されたのである. (p.229) | |||
| 解析的延長を遂行するならば, 全局においては函数の一意性が失われることが可能である. (中略) このような意味での解析函数の多意性は本質的である. (p.229) | |||
| 解析的延長の原則によれば, \(e^z\,\)を拡張して解析函数を得るには, \(e^z\!=\!\displaystyle{\sum_{}\frac{z^n}{n!}}\,\)が唯一無二の方法であることが確定したのである. \(\sin z,\cos z\,\)等に関しても同様である. (p.230) | |||
| 初学者にとって, 解析接続の概念はそれまでの関数の概念を大幅に刷新するであろう. 貞治の叙述は読者に対してその魅力を充分に (文学的な表現をもって) 伝えるものであり, 読者を飽きさせない推進力に富んだものである. |
|||
| さて, 貞治の叙述に惹かれて引用部分が大分長くなったから, 最後に「附録 (II)」における「各所で微分不可能なる連続函数」に触れて次へ進むことにしよう. 貞治は, 微分可能性の必要条件たる連続性が十分条件でない実例として, ヴァイエルシュトラス函数 |
|||
| \(\displaystyle{f(x)\!=\!\sum_{n=0}^{\infty}\!a^n\!\cos\!\:(b^n\pi x)\:\:(0\!<\!a\!<\!1, \:\:b\!=\!2k\!-\!1\,(k\!\in\!\mathbb{N}),\,\:ab\!>\!1\!+\!\frac{3}{\!\:2\!\:}\pi)}\) |
|||
| について言及し (p.39), 附録 (II) において, 同様の例の一つとして (線分の三等分線から得られる正三角形を或る規則で順次付加することで得られる) コッホ曲線を解説した (p.470). その後, 貞治は次のように記している. | |||
| このような曲線があるから, 各所で微分不可能なる連続函数があるといっても, もはやそれは驚くに足るまい (p.39頁参照). このような函数の簡単なる実例を, 筆者はかつて二進法を用いて作った (東京数学物理学会記事, 1903). その後, van der Waerden 君は, 十進法によって, 全く同様な函数を発表した (Mathematische Zeitschrift, 32, 1930). | |||
| ここにおいて貞治が嘗て作った二進法による実例とは, 前節に掲げた [高木3] を指す. いわゆる「高木函数」と称されるものである. 前掲の『定本 解析概論』(pp.509-517) においては, [高木3] に関する丁寧な解説が新たに附記されている (黒田成勝『いたるところ微分不可能な連続函数について』). 現在では, フラクタルの例として頻繁に引用される「高木曲線」であるが,「類体論」と同様, 発表当時は国内外においてほとんど知られていなかったらしい. これに関して, 末綱恕一は, |
|||
| [末綱] 『論文紹介』/『日本數學物理學會誌』 第8卷第8號 (1934年), pp.302-305 | |||
| におけるランダウ (Edmund Landau, 1877-1938) の著書『微分積分學初歩に就て』 | |||
| [Landau] "Einfuhrung in die Differentialrechnun und Integralrechnung" P. Noordhoff N. V., 1934, 全368頁. | |||
| に関する書評の中で, | |||
| 第五章に於いて愈〃導函数\(\,f^{\prime}(x)\,\)を導入する. \(f^{\prime}(x)\,\)を定義すると直ぐに, 到る所連續で何處でも微分出來ない函数 (Weierstrass の定理) を例示する: | |||
| \(\displaystyle{f(x)\!=\!\sum_{n=0}^{\infty}\frac{\{4^nx\}}{4^n}}\:\: (\{y\}\,\)は\(\,y\,\)と之に最も近い整数との距離\()\) |
|||
| 著者は之を今日最も簡單な例で van der Waerden のものと云つて居るので事實\(\,4\,\)を\(\,10\,\)で置換へれば van der Waerden が近頃出したものに相違ないけれども, \(4\,\)を\(\,2\,\)で置換へるならば之は高木先生が數物記事の第一卷に出されたものに外ならない. Landau も van der Waerden もこの卅一年前の論文には全く氣が付かなかつたのであらう. | |||
| と記している (pp.302-303). 貞治は恐らく [Landau] に目を通しているはずである (次節 (§5-6.) で触れる『微積の体系といったようなこと』の中で言及される) から, この箇所におけるランダウの記事に関しては苦笑させられたことであろう. |
|||
| §4-10.『代数的整数論』 | |||
| 前掲の三部作『代数学講義』,『初等整数論講義』,『解析概論』は全て, 東大における貞治の講義に基いて執筆された著作であったが,『代数的整数論』は, 大学での講義とは無関係に執筆された著作である. 執筆当時, 貞治は67歳であった. 実際, 貞治が大学で類体論を継続的に講義することはなかったらしい. 菅原正夫は,「先生は類体論の講義をされたことはありません.」と断言している (前掲書 [追想高木] p.222). 河田敬義『わたしの好きな数学史』(前掲書 [追想高木] p.172) には,「大学では類体論の講義もなかった」と記されているが, 森茂雄『書物は手元に』(同書 p.68) には,「先生の「新著解説」なる講義の一環として (中略) 類体論の講義をされました. おそらく類体論を取り上げられたのは後にも先きにもこの一回だけではないでしょうか」と記されている. また, 彌永昌吉は「東大の最終学年 (1928-29) と大学院では先生のセミナーで類体論を勉強した」と述べている (『類体論50年』(前掲書 [彌永8], p.25)) から, 部分的には大学で採り上げられることはあったのであろう. 私が所蔵するのは, 1994年に発売された重刷版 |
|||
| 『代数的整数論 一般論及類体論』第2版, 岩波書店, 1971, 全307頁. | |||
| である. これは, 私の学生時代には長らく品切れ状態であった. そのため大学生協や近隣の小売店を通して何度も繰り返し発注した後に, ようやく入手したものである.
以下, 引用は全てこの書籍からとする. |
|||
 『代数的整数論』岩波書店, 1971 |
|||
| 既に述べたように,『解析概論』は, 貞治自身の監修による岩波講座 "数学" 全30巻 (1932-1935) に掲載された. 一方,『代数的整数論』もまた同講座において発表され, 後に単行本化されたものである. 副題にもある通り, この著書は, 前篇「一般論」と後篇「類体論」から成り, 詳細なる構成は |
|||
| 前篇 一般論 第1章 代数的整数 (代数体の定義, 代数的整数の性質) 第2章 代数体の整数「イデアル」(イデアルの性質, イデアル論の基本定理, イデアル因子) 第3章 剰余類 (イデアルを法とする剰余類, 剰余類の四則, 剰余類環\(\,\mathfrak{R}(\mathfrak{m}),\,\mathfrak{R}({\mathfrak{p}}^m)\)) 第4章 「イデアル」の類別 (分数イデアル, イデアル類群と類数) 第5章 ミンコフスキの定理の応用 (ミンコフスキの定理, 代数体の判別式) 第6章 相対的の体 (代数拡大\(\,K\!\!\:/k\), イデアルの延長, 共役体, \(K\!\!\:/k\,\)における素イデアル\(\,\mathfrak{P}\!\subset\!K\)) 第7章 判別式 共役差積 (代数体の共役差積, 相対判別式, デデキントの判別定理) 第8章 ガロア体 (分解体, 惰性体, 分岐体, 円体, クロネッカーの定理) 第9章 単数 (ディリクレの単数定理, ガロア体の単数) 第10章 素数進法 (\(\mathfrak{p}\,\)進法, ヘンゼルの補題, \(\mathfrak{p}\,\)の\(\,n\,\)冪剰余) |
|||
| 後篇 類体論 第11章 合同類別 (エルブランの補題, 狭義イデアル類, イデアル群の導手) 第12章 解析的の考察 (合同類別における各類のイデアル密度, 代数体の\(\,\zeta\,\)函数, 類体と円分体) 第13章 基本定理 (アーベル体の基本定理, ノルム剰余と群指数, 結合定理, 類体の一意性) 第14章 分解定理 同型定理 相互律 (アルティンの相互律, 推進定理) 第15章 存在定理 導手定理 (クンマー体, その素因子分解と導手, アーベル体の導手, ハッセの導手公式) 第16章 終結定理 (チェボタレフの密度定理, 終結定理) 附録 (1) 二次体論 (2) 円分体の類数 (3) イデアル論の基本定理 補遺 |
|||
| となっている. この著書にある類体論の概要については前節で既に述べているので, ここでは割愛する. |
|||
| 「序」を見ると, | |||
| 著者が, 1915年以来, 日本数学物理学会記事に断片的に掲載した数編の論文を綜合して, 1920年, 手王匡帝国大学理学部紀要に類体論の全貌を発表してから,
既に四半世紀の星霜を経た. 其の間, (中略) ドイツの少壮数学者 Artin 及び Hasse によって, 類体論の整理簡約が行われたが,
就中 Artin の相互律の発見は類体論への喜ばしい貢献であった. 次で, 珍しくもフランスから, 二人の青年数学者 Herbrand 及び Chevalley が参加して, 整理簡約が進められた. 本書に掲げた類体論の基本定理及び存在定理の証明法は Herbrand に拠り, 又相互律は Chevalley の証明法に従った. 類体論の成果は, 基本定理・分解定理・同型定理 (相互律)・存在定理, いずれも極めて簡単明瞭であるに反して, その証明法は, 上記諸家の努力にも拘らず, 今なお紆余曲折を極め, 人をして倦厭の情を起こさしめるものがある. 類体論の明朗化は, 恐らくは, 新立脚点の発見に待つ所があるのではあるまいか. |
|||
| とある. また, 黒田成勝による第2版の「序」には, |
|||
| 著者高木貞治先生が, 本書の初稿を岩波講座数学に執筆されて以来, それが整数論研究者の精神を力強く高揚して来たことは言うまでもない. 一方微細な点では, 大局の美に魅せられて, 難読難解, 時には誤読誤解をさえ生じた箇所もあった. それらは著者の余りにも高度の暗示的叙述からも, また読者の受容の不全からも生じた. | |||
| とある. 前篇「一般論」は明快で理解しやすいが, 肝心の後篇「類体論」は, 貞治の叙述に問題があるわけではないのであろうが, 大変読みづらく, 理解しがたい部分が少なくない. 無論, 貞治自身の論文 [高木13] における複雑な論理展開に比べれば改善が見られるのであるが……. 貞治自身が「紆余曲折を極め, 人をして倦厭の情を起こさしめる」と述べた所以であろう. フルトヴェングラーや貞治が素数冪の次数に関する相互法則を示したのに対し, アルティンやハッセが一般冪剰余の相互法則を示したことは既に述べた. シュヴァレーが類体論の算術的証明を得たことも既に述べている. 貞治の「序」に登場するエルブラン (Jacques Herbrand, 1908-1931) は, 僅か23歳で事故死した異才の数学者であり,「種の理論」や「一般単項化定理」を含む類体論関係の優れた論文を発表したことで知られている ( [彌永8], p.127). 貞治が「珍しくもフランスから」と述べたのは, かつてのストラスブールでの一件が念頭にあったのであろう. とは言え, 理解困難な貞治の理論が, ドイツやフランスにおける新進気鋭の若手数学者に理解され, 簡約化や算術化が促されたことが, 類体論が人口に膾炙する大きな機縁となったことは間違いない. その辺りの事情を, 貞治は「喜ばしい貢献」と表現したのである. |
|||
| 以下, この著書に見られる貞治の数学思想をいくつか拾ってみよう. まず, 証明における方法の純粋性について――. 第2章における「定理2」すなわち「整係数多項式の積の各係数が\(\,\lambda\,\)の倍数ならば, もとの多項式の各々の係数の積も\(\,\lambda\,\)の倍数である」に関して |
|||
| (前略) 上記証明法は簡明のようでも, 方法上不純な所があることを, 読者は不快に思うであろう. (中略) 目的の為に手段を問わない感がある. (p.19) | |||
| と述べ, クロネッカーの整数論の基礎である定理「多項式の積のイデヤル因子は各多項式のイデヤル因子の積に等しい」に関しても | |||
| この定理 (多項式の積のイデヤル因子は各多項式のイデヤル因子の積に等しい) は Kronecker の整数論の基礎である.「イデヤル」論を使えば, その証明は上記の通り簡単である. この後もこの定理を用いて, 証明を短縮し得る場合があるから, 変数は方法上不純ながら併用する. (p.26) | |||
| と述べる. 論文ではなく書物として執筆する場合, 数学的に純粋 (自然) な方法よりも, より簡明な (晦渋でない) ものを採用せざるを得ないということであろう. 一方, 技術的な問題で回避し得ない方法について, 第7章の冒頭部において |
|||
| 吾々は今代数的整数論に於て解説の最も難渋なる一章に入る. 問題は古くて, しかも基本的であるのに, 整理が不行届で, 心持がよくないのである. (p.61) | |||
| と述べ, デデキントの判別定理に関しても | |||
| この定理の証明は非常に困難であったが, (中略) Hensel (1894) が Krinecker の形式論を用いて比較的に簡単なる証明を与えた. (中略) この方法によって, 2(共軛差積の性質) は容易に得られない. 且又数体\(\,k\,\)の問題を不定文字 (Unbestimmte) を含む整域\(\,k\,[\!\:u_{{}_{1}},\cdots,u_m\!\:]\,\)に引入れるのは, 方法上不純である. (中略) 本書では冗長を厭わないで, いずれの立脚点にも偏倚しないで, 凡ての方法を紹介したのである. (p.82, pp.86-87) | |||
| と述べている. 附録 (3) には,「イデアル論の基本定理」(p.22) の証明に用いた予備定理 (p.18) について, |
|||
| この定理の証明は Dedekind が Dirichlet の整数論講義第四版に附載したものの変形であるが, 既に Dedekind 自身が彼の証明に稍不満の意を表している.
Hilbert が Hurwitz の同僚として Königsberg 大学にあった時, 彼等は当時相携えて散策の途次, (中略)
一人は Kronecker の証明法を論じ, 又一人は Dedekind の方法を語って, 両者共に厭うべきもの (scheusslich)
なるものことに於て意見の一致を見た (後略). Dedekind 以後, 上記予備定理の証明の簡易化が諸方面から試みられたが, 就中 Hurwitz の証明は, 着意の単純, 方法の妥当なる点に於て, 最も興味あるように思われる (後略). (p.291) |
|||
| とある. これらの言明からは, 貞治が, 証明の純粋性 (ないし単純性) に少なからず拘りを見せている様子が窺えよう.『髙等敎育代數學』において, (問題を解く際には) 単に正答を得ればよいのではない, 解法は単純明快を旨とせよと, 学生に注意を与えた貞治は, 定理の証明においても, 単に証明を得ればよいのではない, その方法は自然で妥当であることを旨とせよ, と述べているのである. 同様の言明は p.288-289 にも見られるし, 次節 (§5-6.) で触れる『数学の自由性』においても現れる. 方法の不純性を上手く回避できず「倦厭の情を起こさしめる」にも拘らず「新立脚点を発見」できていないところに, 貞治の懊悩が垣間見えるであろう. また, 表記法や用語に関する注記も幾つか見られ, |
|||
| 「イデヤル」を独逸字\(\,\mathfrak{a},\mathfrak{b},\mathfrak{c}\,\)などで示すのが慣例である. (p.16) | |||
| Landau の記号\(\,2\!\:|\!\:10\,\)は約数を必ず左, 倍数を必ず右に書くことが窮屈である. (p.20) | |||
| (分岐定数) \(v,v^{(1)},\cdots\,\)は Hilbert 報文 に\(\,L,\overline{\!\:L\!\:},\cdots\,\)と記すものである. 運用上は記号を変えて, これらを\(\,v\!+\!1,v^{(1)}\!+\!1,\cdots\,\)と書くのが便利なこともある. (高木, 紀要, 41, 9, §6) (p.100) |
|||
| \(s\sigma\!\:(K)\,\)などは (中略) \(K^{\sigma s}\,\)と書く方が都合がよいが, 印刷上の顧慮から函数記号式にしておいた. 故に\(\,s\sigma\,\)は始めに\(\,\sigma\), 次に\(\,s\,\)を意味する. (p.121) | |||
| (2) に於ける\(\,\mathfrak{m}\,\)は記号として「イデヤル」のように見えるが, それはただ\(\,\mathrm{mod}.\,\)としてのみ使用される.
(中略) それを標示するためには, Hasse のように, 記号\(\,\widetilde{\mathfrak{m}}\,\)を用いるのもよい.
(中略) 意図する所は概念の明確なる表示にある. 言葉では\(\,S_{\mathfrak{m}}\,\)を Strahl modulo \(\mathfrak{m}\,\)という. Strahl\(\!\:\)=\(\!\:\)rayon\(\!\:\)=\(\!\:\)ray\(\!\:\)=\(\!\:\)放射線. 本書では, このような fantastic な造語の邦訳を敢てしないで, 記号\(\,S_{\mathfrak{m}}\,\)を使う. (p.149) |
|||
| などのほか, p.106, p.142, p.146, などにもこの件に纏わる記載がある. ハッセが「基本定理」を「逆定理」"Umkehrsatz" と称したこと,「順序定理」"Anordnungssatz",「推進定理」"Verschiebungssatz",「終結定理」"Abschliessungssatz" がハッセの命名によるものであることも明記されている (p.174, p.194, p.199, p.246). |
|||
| さらに, 数学史上における逸話も幾つか紹介されている. |
|||
| 解析的の方法によって (\(L\,\)函数)\(\,L\!\:(1,\chi_{{}_{i}})\!\not=\!0\,\)を証明したのは Hecke (1917) である. 一方, (合同群)\(\,H\,\)に対応する (類体)\(\,K\,\)が存在すれば, \(H\,\)に関する算術級数の定理が成立って, 従て\(\,L\!\:(1,\chi_{{}_{i}})\!\not=\!0\,\)である (中略) 類体論によって算術級数の定理が確定したとしても, \(L\!\:(1,\chi_{{}_{i}})\,\)の直接証明は当然希望されるものである. 興味のあるのは, 本来の Dirichlet の算術級数の定理は二次形式論によって1837年に証明され, それの解析的証明が Mertens によって1897になされたのに比較して, 一般的の場合に於て, 兩方面の証明が殆ど同時に出来たことである. (pp.171-172) |
|||
| 筆者は紀要論文 (27-62頁) で, 先ず素数次の環状体に関しての証明をして, 素数次の環状体を積み重ねて一般環状体に移乗した. その途も短くない.
素数次の場合の方法が直に一般の環状体に適用され得ることを指摘したのは, 不幸にして登山事故のために夭折した仏国の青年数学者 Herbrand である. (p.191) |
|||
| Artin の相互律は Hamburg の論文集 (Abhandlungen, 1927, 353頁) で発表された. その証明には, 当時の類体論の成果を用いている. (中略) この証明は若干簡易化されて, Hasse の報文 (II, 14-22頁) に載っている. 本書では, 多少躊躇の後, これらを凡て割愛して (直観性を犠牲にして), 相互律の直接証明法を述べることにした. (p.199) | |||
| その他, クンマー体\(\,k\,(\sqrt[l\!\:]{\omega\!\:})\,\)の歴史的位置づけ (p.217) や, クロネッカー式密度\(\,\varDelta(M)\,\)からチェボタレフの密度\(\,\varDelta(\varOmega)\,\)に至る歴史的経緯 (p.244), ディリクレによる二次体および円分体の類数計算に関する叙述 (p.260, p.278) も読者の興味を引くであろう. なお, 上掲の最後の引用箇所における「直観性を犠牲にして」なる所以は, シュヴァレーが, (円の\(\,m\,\)分体)\(K\,\)と (\(K\!\!\:/k\,\)から生ずる円分体)\(\,\varGamma\)とに交截法を二重適用して問題を円分体の場合に帰着させたことによる. 相互律は内容は簡明であるが, 証明は高度に技術的で暗中を驀進するようなものであった. 素でないイデアル\(\,\frak{a}\,\)に対するヤコビ-ハッセの記号\(\,\displaystyle{\left(\!\frac{K\!\!\:/k}{\frak{a}}\!\right)}\,\)が機械的ながらも証明の簡明さを齎す事実は,「類体論の根柢に内在する複雑性の顕現」である. \(K\!\!\:/k\,\)のイデアルのノルムが\(\,k\,\)における群を成すことは自然であるが, これを\(\,k\,\)の全てのイデアル群の部分群として考察することは「むつかしくて, 今の所, 手が着けられない」. しかし, \(K\!\!\:/k\,\)がアーベル体であるときに限り, このノルムの群を\(\,k\,\)の合同群と併せてイデアル群\(\,H\,\)を作ることで類体論は成功したのであった (p.215). |
|||
| それは奇妙だけれども, 事実であるから已むを得ない. そこに秘密があって, それが類体論の非素朴性ともいうべきものであろう. 記号\(\,\displaystyle{\left(\!\frac{K\!\!\:/k}{\frak{a}}\!\right)}\,\)はその秘密を吸収し,
陰蔽して外観上円滑に行動するのである. 古典整数論に於て Jacobi の記号は曾て Gauss の二次形式論の記述を短縮して, 同時にそれを秘密的にした. それは暗中模索の結果であろうが, その秘密は一般「アアベル」体論に由て暴露されてしもうたのである. さて今度は「ヤコビ」式の記号が再び類体論を機械化する. 素朴性と機械化の交代循環! |
|||
| 貞治はこの後も類体を定義する方法に関する興味深い記述を続ける. これらの言明を晦渋な本論と照らし合わせて読むとき, 類体論の煩雑性がもつ深淵かつ不可思議な様相に対する貞治の新鮮な驚嘆の念が読者を刺戟するであろう. |
|||
| 『初等整数論講義』と同様,『代数的整数論』の「附録」においても, 二次体および類数が扱われる. 貞治自身が「二次体論だけの直接の叙述は長たらしくなる」(p.249) と批判するところの『初等整数論講義』第5章の内容 (平方剰余の相互法則および種の理論) が, ここでは類体論の成果を援用して極めて簡明に纏められるのである. 円分体の類数およびガウスの和に関しても,『代数的整数論』の立場から見れば,『初等整数論講義』における叙述法は, 却って迂遠なる説明を余儀なくされている感を否めない. |
|||
| この問題はそれ自身興味深いものであるが, 当時にあっては, 整数論代数学及び函数論の最高部門の交錯する数学の El Dorado である所に, 特に魅力があったのであろう. | |||
| と述べる.「特に魅力があったのであろう」と客観視しているが, 若かりし日の貞治もまた, その魅力に取り憑かれた者の一人であった. 続けて「単項化定理」を簡単に説明した後, |
|||
| 虚数乗法論に於ける実例はこの定理の一般性を示唆するのであるが, ヒルベルトは唯\(\,K\!\!\:/k\,\)が2次の場合及び4次で環状でない場合にのみ証明をしたに過ぎなかった. その後, Furtwängler が群論化された形に於て一般的の証明を与えた. 単項化の問題は未だ成書に取入れられる程度にまで熟していない (後略) | |||
| と述べている. 上掲のフルトヴェングラーの業績については前節でも簡単に触れた. その後の展開については, 黒田成勝『高木貞治先生を敬慕して』(前掲書 [追想高木], p.243) において |
|||
| Hilbert の単項化定理は, Iyanaga によって一般単項化定理にまで拡張せられた. これは単項化定理に関し, ちょうど, Hilbert の類体から先生の一般の類体への概念拡張に相応する拡張で, 先生門下から成しとげられたこの美麗な第一着の発展を, 先生はどんなにか喜びをもって迎えられたことであろう. その後この一般単項化定理のさらに興味ある考察が Tannaka などによって続けられている. | |||
| と記されている. 上掲の「Iyanaga」は, 前節に掲げた論文 [彌永3] であり,「Tannaka」とは, 淡中忠郎 (1908-1986) による |
|||
| [淡中] T.Tannaka "An Alternative Proof of a Generalized Principal Ideal Theorem" Proc. Japan Acad. Vol.25, 1949, pp.26-31. | |||
| である. この件に関する淡中の業績は, 貞治が名誉議長として列席した「代数的整数論国際会議」(1955) における |
|||
| [藤崎] 藤崎源ニ郎『本会議講演記録』/ 岩波書店『数学』第7巻第4号 (1956年10月), pp.203-239. | |||
| に詳しい. また,「単項化定理」に纏わるその後の状況については, | |||
| [三宅] 三宅克哉『彌永先生の数学的な業績』/ 日本数学会『数学通信』第11巻第2号 (2006年8月), pp.44-48. | |||
| に簡明なる解説がある. 『代数的整数論』の巻末には, 黒田成勝による「第2版 跋」がある. その末尾で「類体論」なる名称に関する貞治の懸念が言及されて, この著書は閉じられるのである. |
|||
| 類体論は相対「アアベル」体論に他ならないので, 著者は類体論という名称が, 整数論になにか特別の理論があるような印象を与えやしないかと懸念されたかに見受けられるが, 漢字三字の三綴音である類体論という言葉は, 親み易い名目になっている. つまり, 類体論は, 現今の立場からは,「アアベル」体論なのである. | |||
| §5.著書に見る思想 (2) | |||
| §5-1.『数学雑談』 | |||
| 貞治は, 上述したような代数や解析の専門書を執筆する一方で, 6冊の啓蒙書ないし随筆 |
|||
| 『數學雜談』共立社, 1935, 全264頁. 『過渡期の數學』岩波書店, 1935, 全38頁. 『近世數學史談』河出書房, 1942, 全216頁. 『數學小景』岩波書店, 1943, 全227頁. 『數の槪念』岩波書店, 1949, 全94頁. 『數學の自由性』考へ方硏究社, 1949, 全128頁. |
|||
| を執筆している. 『數學雜談』は,『輓近高等數學講座』および『續輓近高等數學講座』に執筆された数編の記事を一冊に纏めたもので, 貞治がちょうど60歳の時の著作である. [百年史下] によれば,『輓近高等數學講座』は, 1928年4月から1929年10月にかけて刊行され,『續輓近高等數學講座』は, 1930年1月から1931年12月にかけて刊行された (pp.133-134). 出版社は何れも共立社である. 既に記した通り, 現在では『近世數學史談』との合本版も存在するが, 以下の引用は |
|||
| 『数学雑談2版』共立出版, 1970, 全274頁. | |||
| による. |
|||
 『数学雑談』共立出版, 1970 |
|||
| 啓蒙書とは言え, 貞治の執筆姿勢は極めて真摯である. |
|||
| 雑談\(\!\:\)=\(\!\:\)無駄話という古典的公式がある. (中略) しかしながら筆者阿は無駄なるべき話を書く意向を有するのではない. 筆者はこの輓近高等数学講座を一つの「ユニヴァーシテー・エキステンション」(大学延長) と認める. (中略) 大学で数学をする場合には「コロキゥム」なるべきものがある筈である.「コロキゥム」を仮に訳して雑談という. |
|||
| 貞治は冒頭部でこのように述べ, 雑談の中から既成でない新たな数学が産まれる可能性を指摘する. 新たな内容でなくとも, しばらく停滞していたものが,
雑談を通じて何かの機縁で一躍表舞台に躍り出る可能性もあるというのである. |
|||
| 目次から内容を拾ってみると, | |||
| 1. 格子の幾何学 (ピックおよびミンコフスキの格子点定理, クロネッカーの稠密定理など) 2. 平行線の話 (初等幾何における公理の再検討, サッケーリの平行線公理, ポアンカレの擬平面と擬空間) 3. 複素数 (複素数の幾何学および解析学への適用, 代数学の基本定理, 四元数および広延論など) 4. 無理数 (連続の公理, アルキメデスの公理, デデキントの切断, \(\varepsilon\)-\(\delta\,\)論法, 集合論など) 5. 数理が躓く? (ラッセルのパラドックス, カントールの対角線論法, 選択公理など) 6. 自然数論 (ペアノおよびデデキントの自然数論) |
|||
| となっており,『新撰算術』と同様 (あるいはそれ以上に), ここでも貞治が「数の体系」に固執する様子が窺える. これは『數の槪念』で更に深化され, 精密化されることになる. 貞治は, 生涯に亘って「数」の構造を徹底的に追求したのであった. 『新撰算術』と異なり,『数学雑談』には, 読者を一気に惹きつけ最後まで読ませる牽引力がある. それは, 貞治の数学思想および数学史談が随所に示されているからであり, これらも本論に付随する興味深い「雑談」となっているのである. 例えば, 玉突き台を題材としてクロネッカーの稠密定理と天体との関連性 (エルゴード性) を述べたり (pp.28-29), 地上と上空における景観の差異を喩えにして実函数に対する解析函数の経済性を述べたり (p.94), 公理なるものは後から顧みれば明白だが無数の命題から選び抜き公理と銘打つ過程を「冀北の馬群の中から, 千里の馬が見出された」と喩えたり (p.127) する. また, 整列可能定理に纏わる [烏有生] と [青年B君] の対話には, ツェルメロの時代から現在に至るまで続く論争の一端が垣間見える.「万人向きの味付け」を「矛盾を含む要求」とした上で,「100%無味」であるランダウ式の自然数論は, 消化すれば (薬が利いて) 骨まで通る痛味を覚えるが, 味付け無しは「味う勿れ」ではなく「存分に味え」と述べる (pp.243-244). |
|||
| 殊に, 自身の学生時代および著作を回顧するエッセイ (pp.119-122) は『数学雑談』において最も惹かれる部分であろう. | |||
| 1898と1904との間に於いて, 筆者は欧州留学の機会を享受した. 本郷の図書室での独り合点には, 聊か不安がないでもなかったが, 学問の源泉に接触したならば, 源泉の源泉ともいうようなものがあるのではなかろうか, というような空想を抱いていたのである. 1898か1899かにベルリン大学に於ける S. 翁の講筵で Weierstrass 直伝の無理数論というものを, 緊張を以って聴いたこと勿論である. その結果は大なる安定感であった. | |||
| 「S.翁」はシュヴァルツ (前出, §2-4.) を指す. (後に『回顧と展望』に述べられることになる) シュヴァルツによるヴァイエルシュトラス (前出, §2-1.) へ崇拝ぶりは, ここに初出となるのである. |
|||
| 翁は Weierstrass の一言一句を聖典として取り扱う人であったが, 如何に Weierstrass でも, その一言一句が凝固して聖典に化石してしまうのでは, 迅速に時の風化作用を受けずばなるまい.「ケルペル」論に立脚した当時の青年 Dedekind の深みも, 集合論を握っていた青年 Cantor の強みも感得されない. (何トイフ石頭の形式主義デアラウカ!) 青年の心は動き易い. Riemann へ! ゲッチンゲンへ! その頃既に偉才 H. 先生の壮年的禿頭が陸離たる光彩を発揮していたのである. コーシー何者ぞ, ワイヤストラス何者ぞ, 批判的数学の最高峰は, 皮肉にもガウスの Disquisitiones と同じように, 世紀の変わり目に現出した「幾何学原理」ではないか. | |||
| 『回顧と展望』には見られない, 青年貞治の意気込みが熱気を帯びて伝わってくる. なお, 上記引用部における括弧内の文言は, 初版の『續 輓近高等數學講座 2.A』(共立社, 1931, p.3) に見られるもので, 上掲の [2版] では削除されている. 「無理数論に筆を執るのは, 今度が三度目」という貞治は, 一度目の『新撰算術』(1898) は学生時代に乱読した洋書を縦書きに「排出」したもので, 二度目の『新式算術講義』(1904) も「熟慮の遑もなく, 拙速に書い」た. これらの著作はそこに起因する「未定稿」であり, その後二十数年間, 書き直す機会がなかったと述べる. 貞治は, ヒルベルトの『幾何学原理』 |
|||
| [Hilbert3] "Grundlagen der Geometrie" B.G. Teubner, 1899, 全92頁. | |||
| に代表される, 素朴な幾何学的直観によらない無理数論の構築において, 量と数との差別を「克服されたる立脚点」と述べる. しかし,『幾何学原理』が冷遇する連続的な量 (一次元幾何学) を隔離した無理数論は存在理由を欠く. これが, 貞治が『新式算術講義』を執筆した所以であった. |
|||
| 明治37年 (1904) の発行である. やくざな著書の出版年月に拘泥する筆者の偏執を (中略) 弁解する (後略). 思出多き本郷の図書室は1923年の震災に大損害を被って, 遂に取り毀されてしもうた. そこに仮住いの間の「エピソード」であるが, 例の叢書の或る一巻に於いて, Borel が効率的なる解析教程の重要性を高調する序に, Baire の Leçon を推奨しているのを見たのであった. (中略) 繙いて「ギックリ」したのであったが, 早速扉を見て, 1907 とあるので安堵した. しかし緒言の中に「無理数, 極限及び連続性」に関する部分は, 既に1905年に別冊として出してある由が, 記してある. それも1905ならば差支えない. このようなものがあるのに, 1904の新式算術講義が, 1912或は1916では, 著者の立場がなくなる. Baire の Leçon はフランス式の流麗なる「スタイル」で実にみごとに書いてある. Borel が推奨するのも尤もである. あのような立場から無理数論を組立てることは, 筆者も「新式算術講義」で試みたのであった. (中略) Baire の Leçon に於いて望蜀なるは,「具体的量」(Grandeurs concrètes) との連絡が, 解析教程らしく, 投げ遣りに扱われている点である. さて第三回の本稿が再び未定稿的に終るのを筆者は遺憾とするのである |
|||
| 『新式算術講義』における無理数論が貞治独自の工夫によるものであることがここで告白される.『数学雑談』を「決定稿」にしたかった貞治であるが, しかしこれも「未定稿」に終わる運命にあった. 連続的量は斉質的 (各区間が同型) な連続集合であるが, 斉質性は連続集合の必要十分条件ではない. 順序の公理と-連続の公理のみから一次元的連続量を定めることの困難性に直面した貞治は, 次のように述べる (pp.181-187). |
|||
| 本稿に筆を執るに当って, 泥縄式に心当りを当って見たが, 間に合わないで, 止むなく第三回の未定稿を心ならずも書くような仕末になったのである.
(中略) 今時, 無理数論の未定稿を書くのは筆者の酔狂に過ぎない. 終結はしていても如何に終結しているかを問題にして見ただけである. 第四回の無理数論を書くべき機会が筆者に与えられるや否や, 段々覚束なくなるから,「何がこれを未定稿にしたか」を告白して, 筆をおくのである. (昭和五年二月) |
|||
| ところで, ランダウ (ディリクレ) が指摘したペアノの加法の定義における瑕疵を回避する中で, 貞治自身が得た着想 (帰納法によらない加法の可換則と結合則) が解説される (pp.251-252). この手法は貞治独自の工夫によるものであろう.『数学雑談』の初出となる『續輓近高等數學講座 2.A』(共立社, 1930) とほぼ同じ時期に, これに関する論文が執筆されているからである (前節 [高木25] 参照). |
|||
| §5-2.『過渡期の数学』 | |||
| 『数学雑談』の出版と同年の出版物に, 昭和9年の11月に大阪帝国大学理学部数学教室にて開催された貞治による講演4回分を纏めた小冊子 |
|||
| 『過渡期ノ數學 大阪帝國大學數學講演集』岩波書店, 1935, 全38頁. | |||
| がある. 出版されたのは貞治が60歳の時であったが, 講演はその前年に行われたものである. 当時, 大阪帝大理学部では, 学生を対象とした (数学者による) 講演を年に数回, 企画しており, それを「一般社會ノ數學知識ノ進歩に卑益スル所決シテ少クハナイデアラウ」として出版したのであった. 4回の講演は4日連続で行われ, この小冊子の目次は, 過渡期の数学 (11月5日), 解析概論 (11月6日), 数学基礎論と集合論 (11月7日), \(p\)-進数と無理数論 (11月8日) の4項目から成る. 「講演者の辞」として, 貞治は |
|||
| 講演トハイフモノノ, ソレハ學術的ノ講演トイフヤウナソレデハナクテ, ムシロ座談, 或ハ事實ニ卽シテ言ヘバ, 講義室デノ立チ話シデ, 要スルニ, 不用意, impromptu ナル, イワユル漫談トイツタヤウナモノデアツタノデス. | |||
| と述べている. 自身の講演が筆記され, 況してや出版されようなどとは全く想定していなかったらしい. 実際, 各日における講演内容は, 貞治が日頃から抱いている随想のようなものであり,
数学的には特にこれといった纏まりはない. しかし, ここに示される貞治の数学思想はやはり看過できない重みがある. 「過渡期の数学」では, 貞治は, 数学の発展は一様ではない, 即ち |
|||
| first approximation トシテ Treppen-Funktion ト見ラレル. 卽チ階段的ニナツテヰル (圖.1). 進歩ノ速度ハ階段的ニ昇ツテ行ク. 更ニ詳シク云ヘバ圖.2ノ樣ニナルデアラウ. | |||
 |
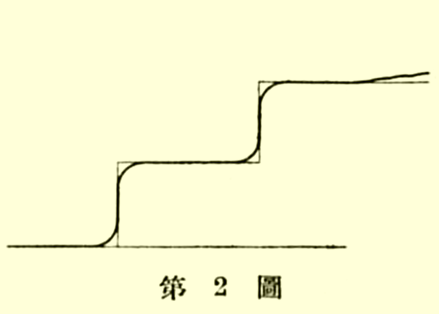 |
||
| と述べ, 階段の直後に数学者の名が密に集まると指摘する. 数学が発展する様子を貞治は川の流れに喩える. しばらく先へ進むと何らかの障害により横に拡がり, 障害を乗り越える高さに達すると一気に勢いを得て流れ出すというのである. ニュートン (Isaac Newton, 1643-1727) やガウス (前出, §2-2.) などの出現は, 数学史の流れに活力を与えたのであった. カントール (Georg Cantor, 1845-1918) は「数学の本質はその自由性にあり」と言った. 真の Freiheit (自由性) がなければ数学において重要な拡張は得られない. 抽象化は拡張の一つであり, 種々の具体的なもの全て含む新たな概念を作ることである. 現代は数学史における過渡期時代 (急激に変化しつつある) と言える. |
|||
| 過渡期の數學ノ特徴ハ第一, 非常ニ急激ニ變ル故少シ懶ケテヰルト分ラナクナル. 興味ノ對象ガ變ツテ來ル. (中略) コレカラ勉強スル者ハ早ク專門ヲキメナイデ深クト云フヨリハ早ク廣ク行ツタ方ガヨイ. 傳統的ノ分類ニヨツテ何ヲヤラウナドト云ハナイ方ガヨイ. | |||
| 貞治自身は, 抽象化を牽引するタイプの数学者ではなかったが, 抽象化の価値を認め, 若い数学者には積極的にこれを学ぶよう奨めていたようである. 彌永昌吉や河田敬義など, 貞治の少し後の時代の数学者達が幅広い数学的教養を身に着けていた背景には, 貞治の少なからぬ影響があったものと思われる. 第2日目の「解析概論」は, 著書『解析概論』に関する言及ではない (この講演時には, この著書はまだ出版されていなかった). 但し, 既に大学においては「微分積分学」の講義を担当していたのであり, 貞治は, 講義の中で得た感慨をここに述べたのであった. 講義で全ての概念や定理を述べる余裕はなく, 内容の取捨選択を要する. 伝統に束縛されることなく, "essential" と "torivial" を見極めた上で,「モツト自由ナ立場デ極ク初等的ナ萬人向キノ解析概論ノ出ルコトヲ希望スル次第デアル.」と結んでいる. 先述したように, 貞治は, 後に『解析概論』を執筆することでこの「希望」を自ら実践したのであった. 第3日目の「数学基礎論と集合論」および第4日目の「\(p\)-進数と無理数論」は,『数学雑談』後半部の内容と重複する. 貞治の疑問はここでも完全に解消されるには至っておらず, その意味ではやはり「未定稿」の感は否めない. |
|||
| §5-3.『近世数学史談』 | |||
| 貞治が著した上掲の啓蒙書における白眉は『近世數學史談』であろう. ガウス, コーシー (Augustin Louis Cauchy, 1789-1857) , アーベル, ヤコビ, ガロア, ディリクレなど, 一流の仕事をした数学者の人物像や業績およびその数学史的な位置づけなどが, 興味深く濃密に描かれる. 貞治流の独特な口上は, 読者を最後まで一気に読ましめる力をもつ. 実際, この著書により感化された数学者が多いことも周知の事実であろう. いや, 数学者に限らない. 本稿の冒頭に挙げた哲学者西田幾多郎 (1870-1945) も, |
|||
| [西田] 西田幾多郎『高木博士の「近世數學史談」』/『西田幾多郎全集 第12巻』岩波書店, 1989, p.235. | |||
| において「大數學者の着眼點とか數學的思想の發展の經路とか云ふものに深い興味を有つた」と述べている. 『近世數學史談』の初出は,『續 輓近高等數學講座 15.A』および『續 輓近高等數學講座 16.C』(共立社, 1931) である. 執筆当時, 貞治は56歳であった. 後にこれは『近世數學史談 輓近高等數學講座 第2卷』(共立社, 1933) として一冊に纏められた. その「序」には, |
|||
| 先きに共立社輓近高等數學講座刊行中社主の要請によつて, 匇卒の間に本編を草した (中略), 意に滿たない所は多いが些少の訂正を加へるに止めた. | |||
| とある. 初出の二分冊には「序」文はなく, 直ちに本文が開始される. 目次の項目を順に列挙すると, 正十七角形のセンセーション, 近世数学の発端, ガウス略歴, 研究と発表, ガウス文書, レムニスケート関数の発見 (\(\sigma\,\)関数, \(\theta\,\)函数), 数学計算とガウス, 書かれなかった楕円関数論, パリ工芸学校, 3つのL., 工芸学校の数学者, コーシー「教程」および「綱要」, 函数論縁起, パリからベルリンへ, アーベル 天才の失敗と成功, ベルリン在留研究生, パリ便リ, アーベル対ヤコビ, 初発の楕円関数論, ガロアの遺言, ディリクレ小伝, 3人の幾何学者, 追記, である. 前掲 (§2-1.) した『近世數學史談』第2版 (河出書房, 1942) においては, 上記本文に若干の言い換えや書き加えがあるほか,『回顧と展望』(附録1),『ヒルベルト訪問記』(附録2) が追加されている. その4年後に出版された,『數學雜談』との合本版 (共立出版, 1946) 所収のものは,『近世數學史談 輓近高等數學講座 第2卷』の再販である. 初版の再販であるから,「附録1,2」は掲載されていない. 第2版の「序」には, この著作に対する貞治の気概が記されている. |
|||
| 振へ振へ, 科学! 與れ與れ, 科学! 行進曲は勇壯である. その裡にあつて, はかない舊稿の校正刷を讀みつつ, 思ふ所なきにしもあらずである. ――科學は何に由つて與るか. ガウスやアーベルは, 手を拱いてその出現を待つ外はあるまい. 國難に促されて隆興した巴里工藝學校は他山の石であるが, そこで物を言つたのは人的「資源」のみである. 數學勃興期の史談が英雄傳に終始するのも止むを得ないであらう……. | |||
| それら英雄の風丯を紹介する小照の挿入は出版所の思ひ付きであるが, 讀者の感興を惹き得るものと信ずる, 旣にガウスが, アーベルの訃音に接して, 肖像が見たいと言つたといふから, 爭はれないものは人情である. そこまでは筆者の史談は行届かない. ゲーテがバイロンの肖像を見たか, 見なかつたか, そこにはエッケルマンの索引でも繰つて見ようといふ手掛かりがある. 年代といひ, 事情といひ, そつくりだから, 興味は一段と高潮する. 楕圓函數發見のローマンスに筆を費やした史談の筆者は, 結局, 椽の下の力持をしたことにもならうか. | |||
| この第2版を現代の仮名遣いに改めた版が |
|||
| 『近世数学史談 3版』共立出版, 1970, 全195頁. | |||
| である. 以下, 引用する際はこの版を (明らかな誤植を修正の上で) 使用することにする. |
|||
 『近世数学史談 3版』(共立出版, 1970) |
|||
| 約200頁に及ぶこの著作のうち, \(1/4\,\)以上がガウスの話題であり (pp.1-57), \(1/4\,\)弱がアーベルの話題である (pp.95-144). 他の数学者と関連する記述を含めれば, 彼らが登場する頁はさらに増える. 貞治は, この二人を主題とした理由を「彼等の口から当時の数学界を語らしめる為」(p.172) と述べているが, やはり貞治自身が特にこの二人に関心を寄せていたのであろう. ガウスの業績は多方面に亘るが, 貞治にとっては [Gauss D.A.] および [Gauss1] の存在が大きかったし,「五次以上の方程式における代数的解法の不可能性」や「楕円関数」におけるアーベルの功績に対しても心酔していたものと思われる. 『近世数学史談』は, 有名な『ガウス日記』の第1項目の引用から始まる. それは, "Principia quibus innititur sectio circuli ac divisibilitas eiusdem geometrica in septemdecim partes etc. Mart. 30. Brunsvigae."「円の等分に基づく原理, それに由って幾何学的に十七等分等々. [1796年] 3月30日. ブラウンシュワィヒに於て」という, 円分方程式論に纏わる正17角形の作図可能性を示唆するものであった. 『ガウス日記』の原著はラテン語で書かれており, 146項目に亘る研究題目のメモが, 1796年3月30日から1814年7月9日にかけて記載されている. 何れの項目についても, 具体的な計算や証明はほとんど記されず, 簡単な研究内容と, 得られた結果のみが記されている. 私が所蔵する |
|||
| [Gauss 日記] "Mathematisches Tagebuch 1796-1814" Verlag Harri Deutsch, 2005, 全234頁. | |||
| には, ラテン語による直筆 (下図参照) および活字の対照表記 (pp.26-63) と, 羅語および独語の対照訳 (pp.66-131) がある. |
|||
 『ガウス日記』第1項目 ([Gauss3] p.26) |
|||
| [Gauss 日記] の冒頭に掲載されたビアマン=クルト (Kurt-Reinhard Biermann, 1919-2002) によるガウスの略伝は, ガウスの生涯と業績, 性格や特徴が詳しく解説されている. また, 後半部には, ガウスに関する研究文献 (pp.134-145) に基いて, 146項目の全てに関して個別に解説が施されている (pp.146-233). 19歳のガウスは, \(x^n\!-\!1\!=\!0\:(x\!\not=\!1)\,\)の根を適当に二組に分けることで円周を\(\,p\,\)等分し得ることを看破した.「高等整数論の研究は今もこの後も数学中最上のもので, 如何程美しい天文学上の発見でも高等整数論が与える喜びに比べれば言うに足らない」と述べるガウスは, 一般論を見出した後, \(p\!=\!17\,\)に関する計算を簡潔に示すのであるが, その計算方法の鮮やかさは読者を驚嘆させるものである. 貞治は,「十七角形でガウスが欣喜雀躍したのではあるまい. 伝説を製造する世間が驚いたのであろう.」と言う (p.10). 実際, 上記の手法を弟子のゲルリング (Christian Ludwig Gerling, 1789-1864) に報告するガウスの口調は, 至って冷静沈着である (貞治が引用したゲルリングへの報告も上記 [Gauss 日記] に見られる).「才に恵まれ寿に恵まれた彼は十九世紀の前半を通じて高く時流を超越して実に一世の泰斗であった」(p.12) と, 貞治も畏敬の念をもってガウスの業績を伝えるのである. 『近世数学史談』に述べられるガウスに関する逸話 (pp.13-28) は, 読者を感化せずにはおかないであろう. 数多くの業績を遺したガウスであるが, 順風満帆の生涯ではなかった.「数学の考究に於ては何よりも妨げられざる, 切り刻まれざる時間が必要」と述べるガウスも, ゲッティンゲン大学天文台長兼数学教授としての観測や講義に時間を割かれ,「まとまった大きい理論的の仕事をする暇がな」く,「その苦しさは言語に絶する」と嘆く. |
|||
| 「思想の豊富なるに比して発表する所の甚だ少なかった」ガウスは「研究の成果が完成されたる芸術的作品の如き形式を具え」ぬうちは発表しなかった, とするザルトリウスの評伝 (前掲書 [Sartorius] ) や,「建築が落成した後に足場が残る」ことを忌避し,「主要部の掛けている建築を提出したくないのであって, 決して外観の美を欲するのではない」とする,
ガウスの弟子シューマッハー (Heinrich Christian Schumacher, 1780-1850) の宛の書簡を紹介する貞治は,
このようなガウスの数学的態度を, 当時の数学界のガウスに対する無理解が原因であろうと述べる. 虚数を用いた証明や非ユークリッド幾何を外に持ち出すことで, 無用な論争や応酬が生じることをガウスは警戒したのである (pp.18-20). |
|||
 C. F. ガウス (1777-1855) |
|||
| 余談であるが, このようなガウスの数学的姿勢を読むたびに, 私は, "Hyperfunction" の創始者, 佐藤幹夫 (1928-2023) を想い出す.「発表する所の少な」い理由はガウスとは異なる. 佐藤の場合は, |
|||
| 木村達雄編『佐藤幹夫の数学』日本評論社, 2007, pp.44-45, p.53 | |||
| によれば, 超函数の萌芽時代, 新たなアイディアをや手法を話題にしてもほとんど理解されないことに失望し, 英語が苦手であったこともあって論文を書かなくなったというのである. 佐藤の理論は, やがて小松彦三郎 (1935-2022) を中心として徐々に若手研究者に理解されるようになったことは周知の事実である. 研究グループの先鋒である柏原正樹 (1947- ) が今年 (2025年) の3月に我国初のアーベル賞受賞者となったことも記憶に新しい. 佐藤のような例は特殊であるが, 一流の数学者たち同士の間では, 新しい理論の構築や新定理の発見に関する先発権争いは熾烈を極める. 同一方面の研究を進めてきた学者達の間において僅かでも他者より発表が遅れた場合は, それまでの研究の価値や労苦は無に帰する. 自力で労苦を重ねて得た成果であっても, 既に流布した研究成果と同程度のものならば, 発表する意義を失うからである. とは言え, 充分に検討することなく先を急いで発表した場合, その論理に僅かでも瑕疵が見つかろうものならば, 数学者として致命傷を負うことになる. |
|||
| しかし, ガウスは定理や理論の先発権には頓着しない. 貞治は次のように記している (pp.21-22). | |||
| 自分では意に満たないから発表しない, いずれその中に暇があったら整理して発表するであろうと, 友人や門弟には告げておく. 他人が発表すれば, それは自分が既に久しき以前, 何年何月に発見していたことだと言う. 知らないものは「うそつき」と思うであろう. (中略) 実際はうそではないのだから, 尚さら憤慨せざるを得ないのである. | |||
| ルジャンドル (前出, §4-8.) が最小二乗法に関して公表した際, ガウスは以前から久しくこれを使用していたと言明し, ルジャンドルを怒らせている. ヤコビが発見した楕円関数についての定理をガウスはその20年ほど前に発見していると知らされたルジャンドルは, ヤコビ宛書簡の中で「ガウス氏ともあろうものが, 貴下御発見の諸定理を, 既に1808年以前に知っていたなどと言いふらす」ことに対し「他人の発見を横奪せんとする厚顔は思量の外」と怒りを露わにし,「斯の如き発見, 予の観る所では数学に於て未曽有なる発見に, 逢着したとするならば, 彼は速かにそれを発表しないでいる筈がない」と断じたという (pp.21-22). この遣り取りに対し, 貞治は, |
|||
| ルジャンドルは所謂発表の先発権に拘泥しているが, 世界は広くて人は様々である. ルジャンドルがヤコービから聞いて知った「未曽有」よりも, ずっと広い意味での「未曽有」をガウスは秘蔵していたのである. | |||
| と記す (p.22). 貞治がここに記す限りにおいては, ヤコビやアーベルにはガウスに対する嫉心は見られない. むしろ, ガウスを目標として励んだという.
ガウスに対する猛烈な妬みや嫉みを剥き出しにするのは, 独りルジャンドルのみである. 楕円関数研究に関してアーベルも同等の研究成果を挙げているとヤコビから聞かされたルジャンドルは, 二人を賞賛すると共に「侵入者G氏などは既に久しく前からそれを発見していななどとは言わないが宜しかろう」,「ガウス氏は楕円関数に関して未だ何も発表していない. (中略) 若しも彼が先を越され, 或は又凌駕されたとしても, それは彼がその研究を秘密の雲に包んでおく報いである」と述べる (p.23). 貞治は, これに関して, |
|||
| アーベルの楕円函数論 (Recherches) がクレルレ誌の第2巻に掲載されたとき, クレルレはガウスにも寄稿を乞うたが, ガウスからアーベルの論文を賞讃する返書を得て, 非常に満足して早速アーベルにそれを知らせている (1828年5月18日)「友よ, 喜べ」というのであるが, このような田舎の気分をパリの老大家などは知らなかったのである. | |||
| と記すのである (p.24). 19世紀の西欧における数学史劇の一端が, 貞治の巧妙な筆致によって鮮やかに活き活きと描き出されおり, 読者にとっては大変に痛快である. [Gauss 日記] に加え, ガウスが遺した学術関連書 (貞治の言う「ガウス文書」) は, ガウスが如何に早熟であったを示している.「Leiste 著の算術教科書」には,「初学者らしい練習問題と交錯して, 当時の数学界では思いも寄らないような独創的の研究」―― 例えば「楕円関数」が記されているという (p.26). ここに現れる「算術教科書」とは, 1790年に出版された, ライステ (Christian Leiste, 1738-1815) の『教育のための算術と代数』 |
|||
| [Leiste] "Die Arithmetik und Algebra zum Gebrauch bey dem Unterrichte" Wolfenbüttel, 1790, 全114頁. | |||
| を指すのであろう. 四則演算から始まり, 冪根計算や代数計算, 不定方程式や高次方程式, 無限級数や連分数などが解説される小冊子である. ガウスの早熟ぶりを貞治は次のように伝える (p.27). |
|||
| ガウス文書を見て驚かれることは, 彼が遠く時世に先行して独自の世界に往したことである. 我々は今更ながらガウスの偉大なる天才を感嘆するのである. 十九世紀数学の最初の飛躍は楕円函数の発見である. 然るにガウスはアーベル, ヤコービに先だつこと三十年にして既に楕円函数を発見している, 少なくとも発見の端緒を確実に把握している. 又デデキンドに先だつこと五十年にして既に modular 函数を発見してアーベル, ヤコービを凌駕しているのである. しかもそれは一例に過ぎない. |
|||
| ゲッティンゲン時代の関係諸氏との往復書簡に関して, 貞治は「当時の数学の活きた歴史の映画ともいくべきもの」と表現しているが, 貞治自身による史談もこれに優るとも劣らないであろう. 中学および高校時代の私は,『レ・ミゼラブル』,『モンテ・クリスト伯』,『アンナ・カレーニナ』などの文学作品に憑りつかれ, 残りの頁が減少していくことを惜しみながらこれらを読み進めた.『近世数学史談』も (これらの名作古典文学とは質は異なるものの) 読了が惜しまれるような著作であることは間違いない. |
|||
| 本節は, 貞治の著書の紹介や書評を目的とするものではなく, そこに見られる貞治自身の数学思想を紹介することであった. とは言え,『近世数学史談』に限って言えば, ある程度の内容を示さなければ貞治の言明は具体性に欠けた空言に陥る可能性がある. 敢えて著作内容を併記する所以である. 貞治は,「ガウス文書」について, ガウスの「完成されたる芸術」の成立過程, すなわち「建築が落成した後に」ガウスが隠そうとした「足場」を暴露するものであると述べ,「アトリエに闖入して自由に下画を掻き廻わすことができる」と述べる (p.28). これに基いて, 以下, レムニスケートの発見に至る経過が詳細に示されるのである. [Gauss 日記] を見ると, 第32項目 (1796年9月9日付) に初めて楕円関数の逆関数が現れ, 翌日 (第33項目) には超楕円積分の逆関数が現れる. レムニスケート\(\,\rho^2\!=\!2a^2\cos2\theta\,\)の弧長\(\,\displaystyle{\int_0^{\rho}\!\!\frac{2a^2\,d\rho}{\!\!\sqrt{\!\:4a^4\!-\!\rho^4\!\:}}}\,\)から\(\,\displaystyle{\int\!\frac{dx}{\!\!\sqrt{\!\:1\!-\!x^4\!\:}}}\,\)を得たのが1797年1月8日 (第52項目) であった. 同年3月19日 (第60項目) にはレムニスケートの\(\,n\,\)等分から\(\,n^2\,\)次方程式が生ずる旨が記され, 3月21日 (第62項目) にはレムニスケートの周を5等分しうる旨が記される. \(n\!=\!5\,\)の場合, 25次方程式の中の (5個の実根を除く) 20個の虚根の意義を求めてガウスは複素函数の考察へと向かったという. この経緯を, 貞治は「函数論の芽生」と記す (p.32). 貞治は, ガウスに関して, 複素数を用いた\(\,s(n),c(n)\,\)の計算, 無限級数や無限積の取り扱いの習熟性, \(\,\log4.81048\!=\!\displaystyle{\frac{\!\:\pi\!\:}{2}}\,\)なる推測 ([Gauss 日記] 3月29日, 第63項目), テータ関数の級数表示, \(e^{-\pi}\,\)および\(\,\displaystyle{e^{-\frac{\pi}{4}}}\,\)の近似値計算など,「ガウスが数字的計算に驚くべき才能を有したこと」を示す種々の逸話を紹介する (pp.29-49). |
|||
| ガウスが如何にしてこれらの結果に到達したかは例の通り明らかでない. (中略) 既成の数学を学修するものは, その容易なる道を歩む (中略). 「幾何学に帝王道路なし」という諺もあるが, 既成数学は実は帝王道路である. 帝王道路の開拓は天才の創意の恩恵であるが, その創意は何処から来るか, それは創意者自身も知らないであろう. 全く天啓である.(中略) しかしそれは僥倖ではあるまい. (中略) 非常なる天才が, 更に非常なる勤勉と結び付いていたのである. |
|||
| ガウスの数学的発見が単なる「僥倖では」ないことは無論である. しかし, その驚嘆すべき数多の業績に鑑みる時, ガウスの「天啓」はやはり豊富なる「幸運」に肖るものと思わずにはいられない. 「算術幾何平均\(\,\mathrm{ag}\!\:\mathrm{M}\!\:(1,\!\sqrt{2\!\:}\!\:)\,\)とレムニスケート関数の周期\(\,\overline{\omega}\,\)との関連性」の発見 ([Gauss 日記] 1799年5月30日, 第98項目) や,「超幾何級数\(\,\mathrm{F}\!\:(\alpha,\beta,\gamma,x)\,\)と\(\,\mathrm{ag}\!\:\mathrm{M}\,\)とモジュラー関数との関係」などの発見もその一例と言えよう. 前者を考察する中で, 楕円モジュラー関数\(\,j\!\:(\tau)\,\)を創出する契機となる求和関数 "summatorische Funktionen" |
|||
| \(\displaystyle{\mathrm{F}\!\:(x)\!=\!\prod_{n\!\:=1}^{\infty}(1\!-\!x^n)}\) | |||
| が登場する (p.55). これは, ガウスの論文『或る特種の級数の総和』 | |||
| [Gauss2] "Summatio quarumdam serierum singularium" Dieterich, 1808, 全40頁. | |||
| において用いられた有理式 | |||
| \(\displaystyle{\mathrm{T}\!\:(x)=\!1\!+\!\frac{a^n\!-\!1}{a\!-\!1}t\!+\! \frac{\!\:(a^n\!-\!1)(a^n\!-\!a)\!\:}{(a\!-\!1)(a^2\!-\!1)}t^2\!+\!\cdots\!+\! \frac{\!\:(a^n\!-\!1)(a^n\!-\!a)\cdots(a^n\!-\!a^{n-1})\!\:}{(a\!-\!1)(a^2\!-\!1)\cdots (a^n\!-\!1)}t^n}\) |
|||
| であり, ガウスはこれを駆使して「遠くアーベル及びヤコービを凌駕」する\(\,j\!\:(\tau)\,\)の基本領域に到り, のみならず\(\,\mathrm{F}\!\:(\alpha,\beta,\gamma,x)\,\)との関係性を含めた理論を構築しようとしたのであった
(pp.50-57). |
|||
| 貞治は, ガウスの研究過程を顧みて次のように述べる (p.57). | |||
| ガウスが進んだ道は即ち数学の進む道である. その道は帰納的である. 特殊から一般へ! それが標語である. (中略) 数学が演繹的であるというが, それは既成数学の修業にのみ通用する (中略) 我々は空虚なる一般論に捉われないで, 帰納の一途に精進すべきではあるまいか. |
|||
| ガウスは77歳で長逝するまでに夥しくも輝かしい業績を遺した. 何れの分野においても, ガウスの手法は本質を突いていた. 理論構築に際し, 他の数学者のように別経路を辿ることなく, 常に最善の路をひたすら邁進した. これは結果論であり, ガウスが最初から意図することは難しいと思われる. やはりガウスは「僥倖」に恵まれていたのである. 先述した通り, 整数論の分野では, ルジャンドルの "Essai" (1798) と [Gauss D.A.] (1801) の対比がある. 貞治は「それらが同時代の著作であることは殆んど想像されない」,「ルジャンドルの整数論は史料としてのみ意味を有するが, ガウスの整数論を我々は百年後に至って漸く消化し終らんとしつつある」と述べ,「そこに数学史上の不連続点の最も著しい実例が提供されている」と述べる. 初等幾何学を講義しつつ平行線公理の証明の必要に迫られたルジャンドルは, 行き詰まりを感じつつ袋小路に嵌り込んでいることを認識できなかったのであるが, 一方のガウスは (先述した理由で公表は控えてはいたが) 非ユークリッド幾何に想いを巡らせた. 後年のボヤイ (Bolyai János, 1802-1860) およびロバチェフスキー (Nikolai Ivanovich Lobachevsky, 1792-1856) による非ユークリッド幾何は, ガウスが既に研究済であった事実が知れるに及んで, ようやく学界から承認されるようになったという経緯をもつ. ルジャンドルはここでもガウスに大きく水をあけられたのであった. 楕円積分に心血を注いだルジャンドルについて, 貞治は「どこまでも不運なる老大家は, 竟に逆函数としての楕円函数を拾うことを得なかった」と述べる. 一方,「幸運なる青年ガウスは, 偶然にも始めから逆函数を問題にしていたが為に, (中略) 決して行き詰らない途を歩いていた」のである. その他, \(\varGamma\,\)函数, (先述した) 最小二乗法, 測地学における非ユークリッド幾何学の実験的証明, 曲面論など, 全てにおいてガウスは大先輩のルジャンドルを遥かに凌駕した実績を示したのであった. これらの逸話を並べた後, 貞治は |
|||
| このような対照に於て, 我々は成心を以って L.を抑えて G.を揚げるのではない. 気紛れな「歴史」が稀に見せてくれる面白い芝居が, ここに演ぜられたのである. 新しい時代は新しい人物に由って興るが, ルジャンドルは恰かも過ぎ行く時代を代表するような位置にいて, 新旧分岐の場面を鮮やかにする役をしたのである. | |||
| と記す (p.66). このくだりは, 読者の心に, ガウスに対する賞讃の念とルジャンドルに対する憐憫の情を抱かせるであろう. とは言え, 上記の逸話は数学史上の事実である. 貞治の文体には (咄家の演じる古典落語のように) 読者を惹きつけてやまない魅力がある. これこそが,『わたしの好きな数学史』(後述する『数学の自由性』に収録されている) において貞治が言うところの「面白い史論」に相当するものなのであろう. |
|||
| ガウスに関する逸話は『近世数学史談』の全編に亘って随所に挿入される. 貞治は, ひと通りガウスの業績や人物に関して記した後, 19世紀のフランス数学界に目を向ける.「三つのL」即ちラグランジュ (Joseph-Louis Lagrange, 1736-1813), ラプラス (Pierre-Simon de Laplace, 1749-1827), ルジャンドルを初め, モンジュ (Gaspard Monge, 1746-1818), ポンスレー (Jean-Victor Poncelet, 1788-1867), フーリエ (Joseph Fourier, 1768-1830), ポアソン (Siméon Denis Poisson, 1781-1840) などに関して言及し, その中で「最も重要なる一人」としてコーシー (Augustin Louis Cauchy, 1789-1857) の名を挙げる. 貞治は「ドイツ人がガウスを看板に出すような所で, フランス人はコーシーをかつぐ. 彼は「フランスのガウス」である.」と述べる (p.79). |
|||
| 彼の思想は断えず揮発せねばならなかった. コーシー全集の巻々を繙く者は精粗錯綜, 玉石混淆に驚かざるを得ないであろう. ここにも「ガウス式洗練! そんな暇は持ち合わせない」人があった. 発表に関して消極的なるガウスと積極を極めたコーシーとは興味ある対照である. | |||
| 貞治による評伝には明記されてはいないが, コーシーが発表に「積極を極め」た理由は先発権争いにあったように思われる. フェルマーの最終定理に関するラメ (Gabriel Lamé, 1795-1870) の手法の横取りと不毛な「似非証明」の応酬は有名であろう. アーベルの才能を見抜けずに彼の功績を無に帰した (p.134) のも, 他者よりもまず自身の功績を優先させるコーシーの自己顕示欲の強さの現れと言えよう. 上記の「ガウス式洗練!」の直前にある「ここにも」とは, p.53 脚注において,「気の早い青年アーベル, ヤコービとは大分違う.「ガウス流の厳格主義!そんな暇があるものか」とヤコービは言うたとやら」を受けての記述であろう. ここで, アーベルに対する「気の早い青年」なる形容は, 読者に誤解を招く可能性がある. コーシーらを中心とする学界から無視されている間に, 自分の得た結論に近い成果を, ヤコビなる若手数学者が発表するのを目の当たりにしたアーベルである (pp.129-131). 貞治は, 他の箇所でアーベルを弁護する (p.132). |
|||
| 当時のアーベルの身になって見るがよい. 彼はガウスのように泰然として先発権などを超越していることの出来る位地に居るのではない. アーベルは「自分ながら驚くばかり多くの発見」をしたけれども,
広い世界にそれを認め得る何人があったか. 旧師ハンステンも親友ホルンボーもアーベルを信じてはいたろう. しかし (中略) 得意らしい高等函数でもパリ学士院に黙殺されているではないか. 楕円函数論はアーベルの最後の切札である. それが思いも寄らない飛入りのヤコービなどに掻き廻されてしもうては, 立つ瀬がないではなかろうか. 借金と肺病とに対抗しつつ, 言葉通り心血を以って書かねばならなかった「楕円積分変形論」である. |
|||
| アーベルには時間がなかったのである. 一般五次方程式の代数的解法の不可能性, (コーシーに放置された) 楕円関数に関するアーベルの加法定理, 楕円積分の逆関数における二重周期性など, 認知されれば一挙に注目を浴びるはずの豊富な数学思想を所持しながらも, その論文の価値を見抜いてもらえなかったアーベルは, 無念のうちに26歳の若さで婚約者に看取られながら結核で世を去ったのであった. なお, アーベルの生涯については, |
|||
| [Stubhaug] ストゥーブハウグ / 願化孝志『アーベルとその時代』シュプリンガー・フェアラーク東京, 2003, 全617頁. | |||
| が最も詳しい. アーベルの死後に彼の元に届いたクレレ (August Leopold Crelle, 1780-1855) の書簡は, 読者を感涙に誘うであろう. 「ヤコービなどに掻き廻されて」なる表現も誤解を招きかねない.「コーシーの紙屑籠に入りそこねた」(p.150) アーベルの論文をヤコビは知る由もなかったのであるから, ヤコビ自身には何の責任もない. 彼も立派な「楕円関数論の創始者」である. 「精力絶倫なる活動家」なるヤコビは, 後に発表されたアーベルの論文『楕円函数の変形に関する一般的の問題の解決』 |
|||
| [Abel1] "Solution d'un problème général concernant la transformation des fonctions elliptiques" Astronomische Nachrichten, Nr.138, 1828, pp.365-387. | |||
| に接して,「我の及ばざる所, 賞讃するに辞なし」として「感激を極め」た (p.133). 貞治も「ケーニヒスベルヒにいる敵手も立派な男であった.」とヤコビを認めている.
ガウスもアーベルの楕円関数論に関しては賞讃したようである (p.51, p.134). その概要を貞治はガウスのレムニスケート関数論と対照させながら紹介する (pp.137-143). |
|||
| アーベルの論文を読むものは先ずその平明暢達で, 少しも巧を求めずして自然に妙なるを愛するであろう. 恰も彼の書簡の天真流露, 親しむべきと一般である (p.137). | |||
| アーベルは |
|||
| \(\,\displaystyle{\alpha=\!\int_0^x\!\!\frac{dx}{\!\!\sqrt{\!\:(\!\:1\!-\!c^2x^2) (\!\:1\!+\!e^2x^2)}\!\:}}\:(c,e\!\in\!\mathbb{R})\,\) |
|||
| として楕円関数\(\,x\!=\!\varphi\!\:(\alpha)\,\)の考察を始め, \(x\,\)を\(\,xi\), \(\alpha\,\)を\(\,\beta
i\,\)としてレムニスケートの弧長と楕円積分を結び付けて加法定理を定めた. 途中, レムニスケートの\(\,n\,\)等分から生ずる「一般等分方程式」が
(\(n\,\)が奇数の場合は) 代数的解法で解き得ることを示し (副産物として得られたアーベル方程式の萌芽), そこから虚数乗法に着眼して乗法公式およびテータ\(\,(\vartheta)\,\)関数の商としての\(\,\varphi\!\:(\alpha)\,\)を得たのであった
(pp.137-142). 貞治は,「アーベルの長所は任意の代数函数の積分に関する所謂アーベル定理の高い立脚点」なるクライン (Felix Klein, 1849-1925) の評に対し,「このような持ち寄りで楕円函数論を合名的に組織するのでは, アーベルの寄与が不当に過大である」とし, 次のように述べる (p.144). |
|||
| ヤコービの\(\,\vartheta\,\)函数, ガウスの modular function と併せて三幅対を作ろうならば, アーベルの虚数乗法が最も適当であろうと我々は思う
(中略) 虚数乗法はレムニスケートの場合にガウスが既にやっているが, \(\vartheta\,\)函数を断えず整数論の問題に応用してガウスを凌がんと力めたヤコービは何と言うだろうか. 彼は他の機会に言うている: 『フーリエ氏などは数学の目的は社会的利益及び自然現象の説明にあると言うが, 氏の如き哲人はすべからく学問の唯一の目標は人間の精神力の発揚 (l'honneur de l'esprit humain) にあることを知るべきである. この見地に於ては, 数の問題も宇宙系統の問題も同等の価値を有するのである』(1830年). |
|||
| ここに引用されたヤコビの言明は,『ヤコビ全集』第1巻 |
|||
| [Jaccobi 全集] "C.G.J.Jacobi's Gesammelte Werke Erster Band" G. Reimer, 1881, 全546頁. | |||
| におけるヤコビとルジャンドルの間に交わされた23通の往復書簡 (pp.385-461) の中の, 1830年7月2日付のヤコビの書簡に現れる
(pp.454-455). 時期としては, アーベルやフーリエ (Joseph Fourier, 1768-1830) が死去した直後である. この書簡の該当箇所の直前には,「熱伝導を優先的に扱わないアーベルとヤコビを非難していた」とするフーリエの言葉を, ヤコビの業績に関する報告書の中に含めたポアソンに対する苦言が記されている. そこへ上記引用部の言葉が現れ, 直後には, フーリエが自身の研究を完成させずに死去したことに対する遺憾の意が表明されている. 貞治がこのヤコビの言葉をここへ持ち込んだ意図は何であろうか. |
|||
| [志村] 志村五郎『数学をいかに使うか』筑摩書房 (ちくま学芸文庫), 2010, p.212. | |||
| によれば, フーリエは, アーベルとヤコビが熱伝導に有用なフーリエ級数ではなく, (それとは無関係な) 楕円関数論の研究を優先させていることを残念に思っていたという.
ポアソンフーリエやポアソンが, ポアソンの結果とヤコビの仕事との関連性を見抜いていれば, 逆にヤコビがポアソンのテクニックを知り得ていたら云々……, とある. 恐らく, 志村は\(\,\vartheta\,\)関数の変換公式とポアソンの和公式の関係を示唆しているのであろう. 上記に引用したヤコビの見解および志村の私見は理解できる. その上でもやはり, 貞治が「ヤコービは何と言うだろうか」としてヤコビの書簡を引用した意図は判然としないのである. |
|||
| アーベルは, その短い生涯全般に亘って, 貧困と結核に加え, 学界から誤解や黙殺を受けるという不運に見舞われた (ガウスと対照的である). 彼が中学生時代に書いた「五次方程式の解法の発見」は若気の至りとしても,『振子の運動に対する月の影響について』即ち, 後に | |||
| [Abel2] "Om Maanens Indflydelse paa Pendelens Bevægelse" Magazin for Naturvidenskaberne" Bd I, 1824, pp.219-226, Berigtelse Bd. II, pp.143-144. | |||
| として発表された論文がシューマッハー (前出) により拒否された (致命的な認識不足を指摘された) のは, ガウスへの門戸を大幅に狭める要因となった
(pp.103-104). その上,『五次の一般的なる方程式を解くことの不可能の証明』は,「証明は略々完全」ながらも「貧乏成る彼は印刷代を節約する為に, 成るべく論文を短縮する必要に迫られて, 説明を十分にする余裕を有しなかった.」 さらに, 標題がいけなかった. アーベルは「代数的」解法の不可能性を意図していた (論文の内容は正にその通りのものである) が, ガウスには「代数的」が抜け落ちて伝わったという (p.108). であるならば, ガウスが論文に目を通したどうかも疑わしい. 後にクレルレ (前出『クレレ誌』) の雑誌発行が始まり, そこに掲載された改訂後のこの論文 |
|||
| [Abel3] "Beweis der Unmöglichkeit algebraische Gleichungen von höheren Graden als dem vierten allgemein aufzulösen" Journal für die reine und angewandte Mathematik, Bd. 1, 1826, pp.65-84. | |||
| には, ガウスも理解を示したようである (p.108, p.111). アーベルの絶筆となった論文は,『或種の超越函数の一般的性質の証明』即ち |
|||
| [Abel4] "Démonstration d’une propriété générale d’une certaine classe de fonctions transcendentes" Journal für die reine und angewandte Mathematik, Bd. 4, 1829, pp.200-201. | |||
| であった. 所謂「アーベルの加法定理」である. アーベルが結核で逝去したのはそれから間もなくであった. |
|||
| ドイツに於てクレルレの運動がフンボルトを動かして, ベルリン招聘の議が将に決せんとしたとき, 1829年4月6日アーベルは溘然として逝いた.
|
|||
| アーベルのベルリン招聘が適ったことをクレルレが如何に喜んだかは想像に難くない. クレルレは直ちにそのことをアーベルに書き送った. しかし, その通知が届いたときには, アーベルは既にこの世の人ではなかったのである (前掲書『アーベルとその時代』参照). |
|||
| ガロアもアーベルと同様, 不運に見舞われて短い生涯を終えた. パリ工芸学校の入試に二度失敗し (p.63, p.146), 入学した師範大学では大学側との悶着の後に放校となった. 過激な政治活動が原因で複数回投獄され,
申し込まれた決闘に負けて21歳で死去したのであった. 翌日に決闘を控えた死の前日, 友人シュヴァリエ (Guillaume-Auguste Chevalier, 1809-1868) 宛に, 方程式が代数的解法をもつ条件 (ガロア理論) および一般アーベル積分に関する新たな定理を書き記した. 同時に「定理の正否ではなく, その重要性をヤコビやガウスに訴えてほしい」とシュヴァリエに訴えたのである (pp.145-147). この「遺書」はガロアの死後すぐに発表されたが,「世上の注意を惹かな」かった. ガロアの方程式論は, 嘗て「ポアソンが異議を挟んだ」が, リューヴィル (Joseph Liouville, 1809-1882) によりガロアの死後14年経ってから公表され, 積分論に至ってはガロアの死後25年経ってからリーマン (Bernhard Riemann, 1826-1866) に発見され, 発表されたのであった. アーベルとガロアを対照させて, 貞治は次のように述べる. |
|||
| ポアソンに抑えられたガロアの方程式論, 叉危くコーシーの紙屑籠に入りそこねたアーベルのパリ論文の運命は奇妙というものであろう. アーベルもガロアも学士院の尻の重さの下に苦悶した. 内気なアーベルは隠忍したが, 高慢なガロアは咆哮した. そこで近世数学史上のローマンスが生じた. アーベルもガロアも処世に失敗したのである. 時代を超越するにも程合いがあって, 二十年, 三十年の超越は危険である. 学士院の尻重きにあらず, アーベル, ガロアの足が軽過ぎたのだ. よい手本に, かのゲッチンゲンの爺さんがある. 賢明というか独善というか, 先生てんで世間を相手にしない. 求むる所のない彼には弱味がない. むしろ求められる位地の強味を (中略) 自家の都合に利用した (後略). |
|||
| 結局,『近世数学史談』は, 独りガウスにのみが群を抜いた栄光に浴したように描かれることとなった. 他に, コーシー, ディリクレなどの評伝も興味深く記されているが, 既にこの著作からの引用も大分長くなったから, 最後に巻末の附録2「ヒルベルト訪問記」に簡単にふれるに留めて次へ進むことにしよう. |
|||
| 1932年10月8日の日付をもつ「ヒルベルト訪問記」は, [追想高木] によれば, 岩波講座「数学」に「書信 (チューリヒ・コングレスの状況, ヒルベルト訪問記」(1932年11月) として発表されたという (p.291).
第9回国際数学者会議のためにチューリッヒに赴いた貞治が, 帰り際に立ち寄ったゲッティンゲンのヒルベルトについて記した書簡体エッセイである. この第9回のコングレスについて, [百年史下] には |
|||
| 世界41ヵ国から約700名の数学者が集まった. 日本からは高木貞治が学術研究会議の代表となり, 他に当時ヨーロッパ留学中の若い三村征雄, 南雲道夫,
弥永昌吉, 守屋美賀雄たちが参加した. 高木は類体論の業績によってすでに著名であり, 11名の副会長の1人として選ばれ, また全体講演の座長の1人に推された.
(中略) 閉会式のときに, 大会委員長よりフィールズ賞の提案があり, 4年ごとの国際数学者会議で2人の数学者にメダルを与えることを決議した. (中略) 第1回のフィールズ賞は次回の会議のときから与えられることになり, その選考委員として, バーコフ (アメリカ), カラテオドリ (ドイツ), カルタン (フランス), セヴェリ (イタリア)(委員長), 高木 (日本) が選ばれた. この会議では会長フェターが開会式演説で特に日本からの遠来の賓客として高木を紹介し, 暖かく迎えた. |
|||
| と記されている (p.56). 余談であるが, 矢野健太郎『第11回国際数学者会議〔1950年〕』(『自然』第6巻第1号, 中央公論社, 1951) を見ると, 第9回 (Zürich) の参会者の数は, 35ヵ国667人, 同行の家族も入れると853人と記されている. ここに現れたフェターこそ, ストラスブール (1920年) での高木の講演で何の反応も示さなかったと先述した (§3-4.) 人物その人である. チューリッヒでの貞治は, 目の前のフェターと12年前のストラスブールでのフェターとの応対差に苦笑させられたことであろう. ここで貞治が出会ったのは, 嘗てのように世界数学界の先陣を切って突き進むヒルベルトではなかった. 難治の重病に冒され弟子達の冷ややかな批判を受けつつも独り寂しく数学基礎論に取り組む, 老いた姿のヒルベルトであった. 「ヒルベルト訪問記」において, 貞治は憐みをもって (しかし畏敬の念を失わずに) 次のように述べる (p.193). |
|||
| 数学基礎論は完成してもよい, 叉は完成しなくてもよい. 只H先生は余生を安楽に送られることを望む (中略) 毎日三十匁の生肝を食って不治の難病と戦いつつも, 駿馬も老いては揚足を若い助手連に時々は取られながらも, どうして排中律の証明等等を書かずには居られないでしょう. 余生を楽しむなどとは論外で, 生きながらの餓鬼道ではありませんか. |
|||
| 最後にヒルベルトに関する微笑ましい逸話が三つほど添えられて『近世数学史談』は終る. (その1) 自宅への来客を迎える直前に, ネクタイを取り替えるよう夫人に促されて二階の自室へ上がったヒルベルト. 客が来訪しても降りて来ないので女中を遣いにやると, ベッドの上で安眠していた由. (その2) ヒルベルトが穴あきズボンを毎日穿いているのに気づいた学生たち. 角が立たぬよう先生に知らせる方法を思案した. ある日, 散歩に出た際, ヒルベルトがトラックの車輪に触れたのを見た一人の学生が, ここぞとばかり「おや, 先生のズボンが痛みましたよ」と伝えると,「ああこれか, この穴は前学期からあいていたようだよ.」 (その3) 自宅に来客を迎えた時の話. 客たちと挨拶や天候の話をして数分が経過した頃, 夫人に向かって「大分お手間を取らせたようだから, もうお暇しようじゃないか.」 これらの逸話に関する貞治の筆致は卓抜である. 貞治による表現は (数学書と同様) 的確で過不足がない上, ヒルベルトの人柄が如実に伝わってくるものである. なお, この書簡体のエッセイの冒頭には「S-君.」なる宛名が記載されている. 架空の人物ならば, その人物を詮索することは無意味であるが, 実在するならば, 貞治に近い数学者の中の一人であろう. 「S君」の可能性として, 苗字で該当するのは, 坂井英太郎, 末綱恕一, 正田建次郎, 菅原正夫などであり, 名前で該当するのは, 中川銓吉, 掛谷宗一, 黒田成勝, 彌永昌吉などである. 後年, 同僚として貞治と親しい関係にあったのは掛谷であるが, 1932年の時点での掛谷は東京文理科大の教授であった. 出版されている対談や談話の記録, 例えば |
|||
| [高木吉江]『高木・吉江兩博士を圍む會』/ 考へ方研究社『高數研究』第3卷第7號 (1939年4月), pp.36-45. | |||
| を見る限り, 貞治が「君」づけで呼ぶのは苗字に対してであり, 直に名前で呼ぶのを見掛けたことはないから, この際, 掛谷 (および中川, 黒田, 弥永) は除外してよいであろう. 坂井は貞治より年齢が上であるから, 貞治が「君」づけで呼ぶ可能性は低い (§2-4. に記したように, 年上の長岡半太郎に対して貞治は「さん」づけで呼んでいる). 一方, 弟子として貞治に近い位置にいたのは末綱であり, 正田, 菅原はまだ学位を得るか得ないかの状態で, (教授または助教授として) 大学には所属していなかった. 1932年当時, 末綱は, 前年にドイツ留学 (ゲッティンゲン) から帰国したばかりの東京帝大助教授であったから,「S君」に該当する可能性は高いが, 確証はない. |
|||
| |
|||
| §5-4.『数学小景』 | |||
| 『近世数学史談』第2版が出版された2年後, 68歳の貞治は, 数学遊戯に関する小著 |
|||
| 『數學小景』岩波書店, 1943, 全227頁. | |||
| を上梓した. これは, | |||
| ・ケーニヒスベルグの橋渡り (一筆書きの可否判定, 迷路脱出法, オイラーの多面体定理など) ・ハミルトンの世界周遊戯 (正十二面体の頂点巡礼, 正十二面体の構成条件など) ・隣組, 地図の塗り分け (四色問題, 平面の塗り分け, 球面およびトーラスの塗り分けなど) ・十五の駒遊び (解法手順の存在問題, 順列と置換) ・魔方陣 (自然方陣の解法, 五進法と五方陣 (超魔方陣)) ・士官36人の問題 (\(n\,\)次オイラー方陣の問題, \(4n\,\)次および奇数次の解法, 半偶数次の検討) |
|||
| を題材として, 初学者でも興味をもって考察し得るように書かれた逸品である. このような専門書以外の啓蒙であっても, 読者を惹きつける話題と話術を縦横に展開する貞治の手腕は見事である言えよう. |
|||
 『数学小景』改版 (岩波書店, 1981) |
|||
| 1943年の [初版] が出た一年後に [再版] が出ている. 誤植や缺落など些細な点はともかく, 貞治にしては珍しく, 数学的な誤謬が含まれていたためである. 1981年に出版された [改版] では, (内容はそのままで) 仮名遣いおよび誤記誤植が改められた. その際, 高木佐知夫 (貞治の三男) による「改版にあたって」なる解題が付加されている. [再販] 出版時における未解決問題で1981年時には解決されていたものもあったが, 内容の改訂は行われていない. 2002年に出版された [現代文庫版] も, (漢数字を算用数字に, 漢字を平仮名に, などの微細な改訂はあるが) [改版] と同一の内容である. 但し,「改版にあたって」は削除されている. 貞治による「序」を見ると, |
|||
| 数学において本質的なるものは, 数学的なる物の見よう, 考え方である. 本書において, 最も簡単なる数個の問題を拉し来って, それらを平易に解決する裡において, 数学的考察法の一斑を説明することが, 著者の意図であった (中略). ただし, 遊戯といえども, 真剣でなくては, 味が出ないであろう. 遊戯は仮託で, (中略) 問題の取扱いに重点が置かれるのである. |
|||
| とある ([改版], pp.vii-viii). この著作で扱われる題材は, 親しみ易いが, 緩やかに思考を巡らさねば理解ができず, 咀嚼吸収しかねるものである.「真剣でなくては,
味が出ない」,「問題の取扱いに重点が置かれる」とは, 取りも直さず貞治自身の数学的姿勢を表現するものであろう. 続けて貞治は記す. |
|||
| 数学には, 雄大な構想もあるが, その雄大は粗大ではない. 極微の抹消においても, 寸毫の齟齬を容さない. 放胆にして, 同時に細心なる所に, 数学の特色があるのだが, いま, 本書で述べる所は, 数学の細心なる方面にある. 題して数学小景という所以である. | |||
| 数学徒以外の一般読者に対しても, 数学に向かう姿勢の最重要点を示す貞治は常に「真剣」である. 遊戯ないし身近な題材をもって読者を惹きつけておき, いざ考察が始まると本格的な数学的姿勢をもって読者を牽引するのである. 初版における貞治の誤謬は, 半偶数次オイラー方陣の問題にあった. 発案したオイラー自身も「多年苦心考究の後, それは恐らく不可能であろうと思われるが, その不可能の証明がむつかしくて, できな」かった ([改版] p.162) という難問である. |
|||
| 6次オイレル方陣の不可能なることは, G.Tarry が試行によって検証したと言われている. その詳細なる報告は, フランス科学協会記事,
1900年号 (中略) に掲載されている由であるが, この文献に予はいまだ属目していない. P. Wernicke (ドイツ数学協会年報, 1910年) は, 一般半偶数次オイレル方陣の不可能性の証明を発表したが, それが誤謬であることが, 近頃指摘された. |
|||
| 最後の「近頃」とは, [再販] (1944) が出版された直前であろうか. あるいは, それ以前に指摘されていたことを貞治が知らなかっただけかも知れない. 貞治は, [再販] が出る直前に, |
|||
| 『オイレル方陣について』/ 岩波書店『科学』第14巻第2号 (1944年2月), pp.42-44. | |||
| において, 誤った証明を『数学小景』に載せたことを読者に詫びている. ところが, 転んでも唯では起きないのが貞治である. この『オイレル方陣について』の後半部では, Wernicke の着想を活かし, ラテン方陣の置換群から得られる群作用によってオイラー方陣の構造を再考したのであった. ところで, 貞治による [初版] の誤謬について, 彌永昌吉は |
|||
| 高木先生は初版を書かれたとき, ウェルニッケの発表をそのまま紹介してしまわれたのである. | |||
| と記し ([現代文庫版], p.187), 続けて | |||
| 初版が出たとき私はおもしろく読み, 誤りなどにも気づかなかった. 少し経ってから誤りを注意してくれた友人があり, 高木先生でも誤りをされることがあるのかと驚いた
(中略). どんなに小さい問題に見えても, 高木先生がこの問題に挑まれたように, 真剣に考えねばならないことを示しているように思う. |
|||
| と記している (同書, p.188). [現代文庫版] にはこの問題に関して編集部による註が付されており (p.177), それによれば, \(n\!\not=\!2,6\,\)なる\(\,n\,\)次オイラー方陣の存在が1959年に証明されたという. 出典は記されていないが, 恐らく |
|||
| [Parker1] "Construction of some sets of pairwise orthogonal Latin squares." Proc. Amer. Math. Soc., Vol.10, 1959, pp.946–951. [Parker2] "Orthogonal latin squares." Proc. Natl. Acad. Sci. U.S.A., Vol.45, 1959, pp.859–862. |
|||
| を根拠にしたものであろう. 単純な問題ながら, 数学史上において興味深い舞台を見せてくれる題材が, ここでも一つ追加されたのであった. |
|||
| §5-5.『数の概念』 | |||
| 貞治が74歳で上梓した最後の著作 |
|||
| 『數の槪念』岩波書店, 1949, 全94頁. | |||
| は,『新撰算術』,『新式算術講義』,『数学雑談』に引き続き, 数の構造を扱った著作である. 数の構造を究めることは, 貞治の (類体論と並ぶ) もう一つの重要な仕事であった. 貞治は, 生涯に亘ってこの問題から離れられなかったのである. |
|||
 『數の槪念』(岩波書店, 1949) |
|||
| その「序」は, 風変わりな書き出しで始まる. | |||
| うちの娘などは, 大學で理科を卒業したのだけれども, \(xy\!=\!yx\,\)など, どうしてさうなるのだか, よくわかつてゐないやうだ.
このやうに, エドムンド・ランダウは, 其の著『解析の基礎』の中に述べてゐる. かうしたことは, うちの娘たちに限るまいから, 一般讀者のために, 解析の基礎として, 數の槪念を, 根本から, 論理的に無缺陥なる體系として, 展開して見せようといふのであらう. |
|||
| 最初の一文は「うちの娘」\(=\)「貞治の娘」を想定させるが, 次の一文で「ランダウの娘」のことだと分かる. すなわち, 数学者シェーンベルク (Isaac Jacob Schoenberg, 1903-1990) と結婚した長女シャルロッテ (Charlotte, 1907-1949), および, 医者 (インディアナ大学医学部教授) になった二女スザンヌ (Susanne, 1908-1982) を指すのであろう. 娘たちも一般的な数学に関しては十分に理解していたと思われるが, とは言え, 基礎論の専門的レヴェルまで要求するのは流石に酷であろう. このランダウの言葉を受けて, 貞治は次のように述べる. |
|||
| 今日, \(xy\!=\!y\!\:x\,\)にしても, \(\sqrt{2\,}\!\cdot\!\sqrt{3\,}\!=\!\sqrt{6\,}\,\)にしても,
周知であらうが, それが何故に然るか. 叉如何にして, それが證明されるか, といふことになると, 話は別である. しかし, 解析學を學ぶものは,
いつか一度は, 根本に立ちもどつて, 數學知識の再檢討をしてみる必要のあることは, 言ふまでもあるまい. さうして, そのとき第一に遭遇するのは, 數とは何ぞやといふ問題であらう. (中略) この問題を平易周到に解説することが, この小册子の目標である. |
|||
| 貞治は, この著作において, (自然数ではなく) 整数の公理から始め, 加法や乗法, 結合則や分配則などを示す. 次に有理数を構成し, 四則およびその稠密性を解き明かす. 最後に, 有理数による収斂数列の極限として, 加法公理を認めた一次元連続体として実数を構成するのである. ヒルベルトの幾何学基礎論における無矛盾の公理系を受けて, 貞治は整数論における無矛盾の公理系を追究した.「序」の末尾には次のように記される. |
|||
| 無矛盾性の證明.「そんなことができるものか」(So was kann man ja nicht.) と, ランダウは勇敢に言ひ放つ (出所上掲). 吾々は謙虚な態度で, そんなことのできるのを待つてゐる. それができた上で, どんなものができたか, ゆつくり檢討することにしても, 晩くはあるまい, と思つてゐるのである. | |||
| §5-6.『数学の自由性』 | |||
| 『數の槪念』と同年に出版された |
|||
| 『數學の自由性』考へ方硏究社, 1949, 全128頁. | |||
| は, 1936年から1944年にかけて執筆した数学評論ないし随筆を一冊に纏めたものである. これらの初出は, 藤森良蔵 (1882-1946)
主宰による数学誌『高數硏究』(考へ方硏究社) および受験雑誌『考へ方』である. |
|||
 『數學の自由性』(考へ方研究社, 1949) |
|||
| 貞治による「序」と巻末には藤森良夫 (良蔵の長男) による「高木貞治先生への感激」なる一文がある. ここには, 戦後『考え方』に発表された「數學の自由性 」および「考へ方のいろいろ」のほか, |
|||
| ・數學漫談――わたしの好きな數學史 (第1卷第1號, 1936.10, pp.3-4) ・數學漫談――彼理憤慨 (第1卷第1號, 1936.10, pp.4-5) ・數學漫談――微積の體系といつたやうなこと (第2卷第3號, 1937.12, pp.1-4) ・Newton. Euclid. 幾何讀本 (第3卷第4號, 1939.1, pp.1-5) ・日本語で數學を書く, 等々 (第4卷第1號, 1939.10, pp.2-4) ・數學の應用, それの實用性などといふこと (第5卷第1號, 1940.10, pp.1-4) ・或る試驗問題の話 (第6卷第1號, 1941.10, pp.1-3) ・昔と今 ―― 圓周率をめぐつて (第7卷第1號, 1942.10, pp.1-10) ・數學の辻説法 (第7卷第8號, 1943.5, pp.1-2) ・數學の實用性 (第7卷第11號, 1943.8, pp.1-5) ・蟲干し (第9卷第1號, 1944.10, pp.39-42) |
|||
| が掲載されている (括弧内は,『高數硏究』掲載関連情報). 『高數硏究』は, 1936年10月から1944年12月まで発行された月刊誌である. 第1卷第1號の冒頭において, 藤森は「發刊の辭」に続き,「高數硏究發刊の趣意」として, |
|||
| (前略) 昭和維新の達成が獨創發明の完遂にまつ以上, (中略) どうしても具現しなくてはならぬことは, 高等數學としての微積分を知つてゐる人を,
中等數學としての代數幾何を知つてゐる人の數位に到達せしむる事である. (中略) 高等數學入門, 大學數學解放をスローガンとして雜誌「高數硏究」を創刊することにした. |
|||
| と, かなり困難度の高い目標を掲げている (p.2). その内容については, | |||
| (前略) 高等數學の平易化, 大學數學の解放を目標として本誌を發行する次第でありますが, 高等數學をやるといふ以上, 何と云つても高等學校程度としての高等數學
―― 解析幾何, 微積分或は高等代數, 三角法といふものに對するしつかりした根柢を作つておくことが大切であります. (中略) 卷頭の論說としては, 日土大學講師諸先生並びに其他の権威ある方々から原稿を頂き, 明快且つ嚴密なる數學の眞の姿に接すると同時に, 數學を學ぶ者への正しき指針を示して頂くことになつてお居ります. |
|||
| とある (p.2). ここに登場する「日土大學」は, 藤森が創設した一般人を対象とする講座である. |
|||
| [高木末綱]『高木末綱兩博士を圍む日土大學座談會』/ 考へ方研究社『高數硏究』第6卷第11號 (1942年8月), pp.26-35. | |||
| を見ると, 貞治や末綱を中心とする数名が, 日土大学の現状と今後の在り方を論じている. 正規の大学生ではないが大学の数学に興味を有する一般人を相手に, 入門的な講義をなすことが目的であったらしい. 余談ながら, この座談会の中で, 次節で触れる矢野健太郎 (1912-1993) の名が現れる. |
|||
| 藤森良蔵:矢野健太郎君なんかずつと始めから日土大學をきいてゐて, 去年日土大學の先生になつて非常にしつくりした講義が出來たといふことは, やはり會員の心理狀態を知つてゐるからですよ.
(後略) 高木:矢野がいつ聞いたんです? 藤森良蔵:新制にならない前からずつと聴いて居られたんです. 高木:君のところと關係があるんですか? 藤森良蔵:ええ, 雜誌の懸賞問題なんか熱心にやつてをられました. (中略) 藤森良夫:(前略) 川上圭介といふ人は, 丁度矢野君と同じくらゐの年配だ (中略). 高等學校の準備時代に「考へ方」の懸賞問題を熱心に應募したんです. (中略) 矢野君はその川上君達と一緒だつたんですから, その賞を互ひに爭つたものなのです. (中略) |
|||
| 貞治が定年退官した1936年当時の矢野は大学院生であり, この座談会が開かれた1942年当時の矢野は30歳で東大の講師であった. 掛谷や吉江などの同僚に対しては「君」づけにしていた貞治が, 学生ないし講師であった矢野に対しては呼び捨てにしている点が注意を引く. さて, 上記引用部にある「権威ある方々から原稿を…」の通り, 続く3頁から5頁にかけて,『數學漫談』と題する貞治の随筆が二つ (『わたしの好きな數學史』,『彼理憤慨』) 掲載されている. |
|||
| 『數學の自由性』の「序」を見ると,「『高數硏究』及び『考へ方』に掲載された雜文に多少筆を加へたものの集錄」とある. この著作の標題の由来でもある最初の小論『數学の自由性』(pp.1-16) では, カントールの言葉「數学の本質はその自由性にあり」が数学史上において如何なる状況で発せられたか, その経緯が具体的に示される. 後半部では, 数学史上に発生した順序そのままに学んだ貞治自身の学生時代にふれ, それは伝統に縛られた不合理な方法であると解く. 続く『考へ方のいろいろ』(pp.17-22) では,「ゼノンの逆説」の解説および時計の針が重なる時刻に関する軽い話題が展開される. 貞治の言う『わたしの好きな數学史』(pp.23-25) は,「正確なる史實の記錄」である. しかし,「(數学) 史論は各人各樣でなければなら」ず, 貞治は「面白い史論」を好むという. 貞治はこう述べた数年後に,「面白い史論」としての『近世数学史談』を自ら執筆したのであった. 『彼理憤慨』(pp.26-29) では,「極限だの収斂だの」に「構わ」ず「\(\displaystyle{\sqrt{\!\:1\!+\!x\,}\!=\!1\!+\!\frac{x}{\!\:2\!\:}}\,\)でよい」としたペリー (Matthew C. Perry, 1794-1858) の姿勢を引き, その「核心」である「數学の實用性」について,「人生は短いけれども, 多くの實用主義は人生よりも短命である」と述べる.「微に入り細を穿つよう理論を講ずる學術主義」や「理論を無視した極端なる實用主義」を斥け, ペリーが狙う数学教育改良講壇に関して, 貞治は, 彼らの抱く高遠な理想へ徐々に収斂することを信じると楽天する. ペリーは憤慨するが, 貞治のような「樂天家は憤慨しない」のだという. |
|||
| 『微積の體系といつたようなこと』(pp.30-39) は, 全篇中, 最もユーモアに富んだ逸品であろう. これも,『高數硏究』第2巻第3号においては『數學漫談』と銘打って掲載された. 内容は, 解析学における基礎的な話題であるが, 上記の矢野健太郎との関連で次節 (§6-2.) で触れる関係上, その内容を少し詳しく見ておくことにする. なお, 初出の『高數硏究』と単行本『數學の自由性』とでは, 表記や内容に関して若干の異同がある. ここでは前者からの表記を採用しよう. |
|||
| 本誌の爲に何か書けと, Nにせがまれ出したのは, 何でも蘆溝橋の頃であつた.「何分, この暑さではね.」で, あつさり撃退した積りでゐたのが, 不覺であった. 逆が必ずしも眞でないことを知らぬ顔に,「昨今は大分秋らしくなりました」ことを指摘するNである. 形勢は宜しくない. | |||
| 冒頭部において貞治はこのように記す. 藤森良蔵は貞治にたびたび『高數硏究』への寄稿を依頼した. とは言え, この著書において初登場となる頭文字「N」なる人物が誰なのかは判らない. |
|||
| 形勢は單調に惡化した. 竟には「書くことがないから, 書かない」などと, 丸で借金の言譯でもするやうな破目に陥つた. しかしながら, 僕といへども, 日本男児のはしくれだ. 外交が下手で, 借りもしない借金を背負込むやうだが, かうなれば潔よく自腹を切つて見せようと, 決心をして居たのである. | |||
| 数学とは何の関連もない「漫談」が続くが, ほかでもない, 貞治の「漫談」であるからこそ, 読者は飽くことなく読み進められるのである. |
|||
| それは小春日和の或る午後であつた. このやうな條件の下に於て, 僕の場合, 一般的には, 慢讀は甘睡に收斂するのであるが, 上記午後は特異であつた. 僕はハツとした, ハツとして發見をした. 借金を返す工面がつきさうなことを發見したのである. | |||
| これまで, 驚嘆すべき理論や美しく鮮やかな解法を展開した際にも決して大風呂敷を拡げなかった貞治が, ここでは些か昂奮ぎみに読者の注意を引いている. 以後, 例の「N」と, もう一人の人物「O」との対話形式で話は展開される.「O」は, 自宅で雑誌の整理をしつつ何気なく頁を捲っていて「ハッとした」のだという. |
|||
| N.朝寝の後に晝寝, その忙がしい中で, 何をページつて, 何を發見したのですか. ――これですか Mathematische Zeitshrift, 40. 一つの連續函數について. Hermann Schmidt. Jena の住人. ページ70-71. こんな短いもので, 逃げようと言ふのですか. |
|||
| 会話の発端は, ドイツの数学誌に掲載されたシュミット (Hermann Karl Schmidt, 1902-1993) の論文 |
|||
| [Schmidt] "Über die Stammfunktion einer stetigen Funktion" Mathematische Zeitschrift, 1936, pp.70-71. | |||
 シュミット『連続関数の不定積分について』冒頭部 |
|||
| である. 要は,「微分積分学の第一基本定理」即ち「有界閉区間\(\,I\!=\![\!\:a,b\,]\,\)で\(\,f\!\:(x)\,\)が連続ならば, \(I\,\)において連続関数\(\,F\!\:(x)\,\)が存在して\(\,F^{\prime}(x)\!=\!f\!\:(x)\).」(定理 (A) とする) の証明法に関する話題である. |
|||
| O.何の変哲もないやうだが, S君はそこに變哲を發見したのだ. S曰く, (A) は問題としては微分學!の問題だ. (中略) この微分學の問題を解くのに, 現今はリイマン積分の可能性といふやうな積分學の定理を用ゐて大迂回をしてゐるのが, 心持が惡い, とSは言ふのだ. ビ分のことはビ分でせよ, と修身で敎はつたではないか! そこで, S氏は某年某學期に, 初級生の爲の講義に於て, 定理 (A) を微分學で說明したさうである. |
|||
| 『ヒルベルト訪問記』と同様, ここでも「S君」が登場する. この場合の「S」は, 言うまでもなくシュミットを指すものである. [Schmidt] の冒頭部 (上掲) を見ると,「任意の連続関数\(\,f\!\:(x)\,\)は原始関数\(\,F\!\:(x)\,\)の微分と看做せる」なる定理は, 本来は微分の範疇における証明が望ましい, これに基く1934年の夏学期の初心者向けに行った講義の内容を紹介したい, とある. 無論, ここには,「大迂回」が「心持が惡い」とか「ビ分のことは…」云々なる文言は見られない. 当時のドイツに「修身」なる授業があったかどうか, 私は知らない. これらは貞治流のユーモアであろう. |
|||
| N.あゝ分かりました. あれでせう. 微分學と積分學, 神奈川縣と靜岡縣だ. 蘆の湖の水面にも神奈川縣と靜岡縣との境界がある. 境界がある以上は, 神奈川縣の鑑札を持つた船なら, 神奈川縣と蘆の湖の交はり, Durchschnitt に於て, 止まり, 走り, 叉は沈沒すべきである. 同樣に靜岡縣の鑑札……, 所で, その人, 靜岡縣の土木課ですか? O.氣の早い男だ. しかし, 何も箱根くんだりまで行かずとものことだ. 新聞で讀んだらう. 數寄屋橋の中程に行倒れがあると微分署と積分署との間に管轄爭ひが起るといふではないか, それは「おれは知らんぞ」といふのださうだが, Sの場合は (A) を微分署へ引取らうといふから, 殊勝ではないか. |
|||
| \(f\!\:(x)\,\)の連続性から, \(f\!\:(x)\,\)に各点収束する\(\,f_n(x)\,\)が線分の接続により得られる. 放物線の弧の接続として適当に\(\,F_n(x)\,\)を作り, \(F^{\prime}(x)\!=\!f_n(x)\,\)とできることは明白であろう. そこで,「項別微分の定理」すなわち「\(\,I\,\)で\(\,F_n(x)\,\)が各点収束し, \({F^{\prime}}_{\!n}(x)\!=\!f_n(x)\,\)が\(\,I\,\)で一様収束するならば, \(F_n(x)\,\)は\(\,I\,\)で収束し, その極限を\(\,F\!\:(x)\,\)とすれば\(\,F^{\prime}(x)\!=\!f\!\:(x)\).」(定理 (B) とする) を用いれば, 定理 (A) が得られる. なお, 些細なことであるが, 後に出版された単行本『數學の自由性』では, 上記の「N」の最後の台詞「同樣に……土木課ですか?」は削除されている (続く「O」の台詞にも若干の言い回しの違いが見られる). 一方, 上記の「N」台詞の冒頭には, 単行本において追加された台詞がある (下記の下線部). |
|||
| N.あゝ分かりました. あれでしよう. sectionalism, 割拠主義というやつでしよう. 微分學と積分學, 神奈川縣と靜岡縣だ. (以下略) | |||
| この一文が追加された理由は不明であるが, これが発表された1949年当時 (戦後民主主義が発展しつつある中), 戦前に各地を席捲した軍閥割拠や国家レヴェルでの
"sectionalism" を想起させることで,「嘗て流行した」即ち「現代にあっては時代遅れ」なるニュアンスを醸し出そうとしたのかも知れない.
何れにしても, 次節 (§6-2.) でこの部分が引用される関係上, この追加された台詞の部分を附記しておく. |
|||
| O.Sさんは連續函數の平等連續性と, よく知られた定理 (B) と, そんなものだけで, 積分なんかに觸れないで, 神奈川縣内に於て (A) に達したのだ. N.成程面白いですね. O.感心したらう. 所で定理 (B) だね. あれは, どうして證明するのだつたかなあ. (中略) \(f_n(x)\,\)が連續ならば, 積分をすれば, 直ぐに證明が出來る. Sの場合, 折角\(\,f_n(x)\,\)は連續だけれども, 不幸にしてその積分が封ぜられて居る. さうすると (B) の證明はむづかしい. (中略) S君は\(\,f_n(x)\,\)の連續性を利用して, 何かうまい考案があるのかな. |
|||
| 「O」自身はS何某氏が如何にして「定理 (B)」を証明したかに関しては知らないらしい. [Schmidt] では, 最初の頁 (p.70) の脚注において, [Landau] の「単純だが本書の中で最も難しい」という「定理344」が挙げられるのみである. ところがこの後, この「O」自身は, 積分せずに定理 (A) に達する方法があると述べる. 区間\(\,I\,\)の分割\(\,[\!\:x_{i-1},x_i\!\:]\,\)の最大値\(\,\mu_i\,\)を用いた\(\,\displaystyle{\small{\sum}\,\mu_i\!\:(\!\:x_i\!-\!x_{i-1})}\,\)は各分割に関して有界であるから, その下限\(\,S\,\)に対し, \(\,[\!\:a,x\!\:]\:(x\!\in\!S\!\:)\,\)における\(\,S\!=\!S\!\:(x)\,\)が\(\,I\,\)において確定する. これは連続で, 実は\(\,f\!\:(x)\,\)の原始関数になっているというのである. |
|||
| N.當前でせう. 積分をすれば, 原始函数は得られませう. O.所が積分はして居ないのだ. 例の和\(\,\displaystyle{\small{\sum}}\,\)から極限へ行けば, それは積分さ. しかし吾々は極限へ行かなかつた. 吾々は下限へ行つて踏止まつた. 靜岡縣へ間一髪と言ふ所だね. (中略) Sさん曰く, あれは神奈川縣だ. 積分は確にして居ない. (中略) N.その下限と最大値とだけで, 原始函数を出すといふのは, 誰が考へたのですか. O.それは知らないね. Sは Landau の「手引き」に出て居るといふ. (中略) 出典調べにも及ぶまい. 旣に Vallée-Poussin の解析敎程に出て居る. あの爺さんなんか, 平氣なものだ. 連續函數の積分を定義する方法は, いくらもあるが, 最も手近なのは, 例の和卽ち\(\,\displaystyle{\small{\sum}\,\mu_i\!\:(\!\:x_i\!-\!x_{i-1})}\,\)の下限であらう. (中略) それを積分と名づけやう, といつた調子で, 心地よく, ドライヴ・ウエイをしてゐる. 縣の境界なんか無視して (後略) |
|||
| ここに現れるランダウの「手引き」とは前掲の [Landau] すなわち『微分積分学入門』であり, ヴァレ・プサン (Charles-Jean de La Vallée Poussin, 1886-1962) の『解析教程』とは |
|||
| [Vallée Poussin1] "Cours d'analyse infinitésimale Tome I" A. Uystpruyst - Dieudonné, 1903, 全372頁. | |||
| [Vallée Poussin2] "Cours d'analyse infinitésimale Tome II" A. Uystpruyst - Dieudonné, 1903, 全440頁. | |||
| である. 以上が, 初出誌『高數硏究』に掲載された記事である. ところで, 以上の内容のみであるならば, 標題『微積の體系といつたやうなこと』の趣旨が判然としない. そこで『數學の自由性』pp.37-39 を見ると, 以上の記事に続けて, 後に追記された貞治の所見が掲載されている. 以下, そこから引用しよう. まずは,「微分, 積分」の名称についてである. 明治時代以降,「微分法, 積分法」と称していたものが, いつの間にか「微分學, 積分學」なる名称が流布していることを貞治は疑問視する. 英米ではこれらを一括して "calculus" と呼ぶ. これに倣って我が国でも「微分積分法」あるいは「微積」でよい, と述べるのである. 続いては,「微積分の體制」すなわち「初學者」へ「微分積分の手引き」をする手段についてである. 貞治は, |
|||
| 微分と積分とを切り離し叉は對立させて,「微分のことは微分でする」といような考え方は不適切であろう (中略) 兩手ですれば具合よくできることを强いて片手でしてみたり, 兩足でらくに歩けるのを片足で跳ねて行くというようなことは, 特別の理由がない限り, 無益な難行苦行といふものであろう. S氏の指摘したことはたしかに面白い. 微分學の先生を喜ばせるに十分であろう. 喜ぶのはよいが, それを直に敎養學部の講義でやつてみるのは行き過ぎというものだ. そういうやり方を例の彼理などは批難するのだ. |
|||
| と述べる. これが貞治の主張したかった「微積分の體系」であった. 『解析概論』を執筆する中で, 貞治はその叙述法に関して種々の工夫を凝らした.「教本式」か「講義式」か, 歴史の流れに沿う形か, 天下り式を含む効率主義的な形か. 何れの形態を選ぶかは, 時代に趨勢に沿った執筆目的や出版事情その他の要因により左右される. 「一般向きの解析学予修書」ないし「解析学読本」として執筆された『解析概論』において, 貞治は, (上記の定理を含め) 可能な限り平易で単純な手法を採用したのである. 時代の変化の中で後に批判に晒されることになるのも想定済みであったことであろう. |
|||
| 『微積の體系といつたようなこと』のような「O」と「N」との対話形式は, その後も『Newton. Euclid. 幾何讀本』(pp.40-50),『應用と實用』(pp.64-71),『或る試驗問題の話』(pp.72-78) などで採用される. 落語を聴くかのような丁々発矢の遣り取りが読者を惹きつけて離さない. 無論, 内容に関しても, 数学史上における逸話 (『Newton. Euclid. 幾何讀本』(pp.40-50)), 数学用語の名称 (『日本語で數學を書く, 等々』(pp.51-63)), ガウスやフーリエによる計算の工夫例 (『數學の實用性』(pp.104-118)),『蟲干し』(pp.119-128) など, 読者を感心させる話題が豊富である. このガウスによる計算例は,『近世数学史談 3版』p.45 にあるものと同一である. その紹介の後, 貞治は |
|||
| ガウスの手に掛かると, 整數論が實用的になる. 若しも吾々がその眞似をして, 何か妙案はないかなどと考へていた日には,「下手の考え休むに似たり」で,
時間の徒消に終るでしよう. それは不實用の極端でありましよう. ガウスの話をしたのは, 實用は物に在らず, 人に在り. 徹底的なる理解の上に於てのみ, 眞の實用は可能である, ということの一例を擧げたのであります. 吾々凡人にはガウスの眞似は出來ない. しかしガウスの精神を眞似ることは出來る. (中略) 世ニ用アリヤ, ナシヤなどと大それたことを考えないで, 身分相應の所で最善を盡くすこと. これが吾々に與えられたる唯一の途でありましよう. |
|||
| と結んでいる (p.118). 現代においても「数学の実用性」を云々する者達は少なくない. その多くは, 概して数学に対する無理解 (苦手意識を纏った)
者達である. 貞治のこの見解を是非, 味わって頂きたいものである. この著書の中では,『昔と今 ―― 圓周率をめぐつて』(pp.79-99) が興味深い. 円周率の計算は, 実用的な必要性もあって, 古代から多くの人々の興味ある対象であった. アルキメデス (Archimedes, 紀元前287-212) は正九十六角形の周を考察して\(\,\displaystyle{3\frac{1}{\!\:7\!\:}\!>\!\pi\!>\!3\frac{10}{\!\:71\!\:}}\,\)を得たという. また, マチン (John Machin, 1680-1751) は, 初等的ながら極めて巧妙なる計算によって得た |
|||
| \(\displaystyle{\frac{\!\:\pi\!\:}{4}\!=\! 4\mathrm{Arc}\tan\frac{1}{\!\:5\!\:}\!-\!\mathrm{Arc}\tan \frac{1}{\!\:239\!\:}}\) |
|||
| を用いて小数点以下100桁まで計算したという. 貞治は, このマチンの公式を, \(\displaystyle{\frac{1}{\!\:1\!+\!x^2}}\,\)の冪級数展開の\(\,0\,\)から\(\,x\,\)までの項別積分\(\,\mathrm{Arc}\tan
x\,\)から\(\,\displaystyle{\tan\!\left(\!4\mathrm{Arc}\tan\frac{1}{\!\:5\!\:}\!-\!\frac{\!\:\pi\!\:}{4}\!\right) \!=\!\frac{1}{\!\:239\!\:}}\,\)を用いて得る方法を紹介している. \(\,\displaystyle{}\,\)シャンクス (William Shanks, 1812-1882) もこの公式を用いて707桁まで計算したが, 第528位以下に誤りがあったことが後に判明したようである (『數學』第1卷第1號, 岩波書店, 1947, p.45). |
|||
 『数学』第1巻第1号 p.45 より引用 (執筆者不詳) |
|||
| また, オイラー (Leonhard Euler, 1707-1783) は, 極めて技巧的なる計算によって得た |
|||
| \(\displaystyle{\frac{\!\:\pi\!\:}{4}\!=\! 5\mathrm{Arc}\tan\frac{1}{\!\:7\!\:}\!-\!2\mathrm{Arc}\tan \frac{3}{\!\:79\!\:}}\) |
|||
| を用いたが, マチンよりもうひと工夫を加え, 収束するスピードの速い | |||
| \(\displaystyle{\frac{\!\:\pi\!\:}{4}\!=\! \frac{7}{\!\:10\!\:}\left\{\!1\!+\!\frac{2}{\!\:3\!\:} \!\cdot\!\frac{2}{\!\:100\!\:} \!+\!\frac{2\!\cdot\!4}{\!\:3\!\cdot\!5\!\:}\left(\!\frac{2}{\!\:100\!\:}\!\right)^2\!\!\!+\!\cdots \!\right\}\!+\!\frac{\!\:7584\!\:}{\!\:10^5\!\:} \left\{\!1\!+\!\frac{2}{\!\:3\!\:}\left(\!\frac{144}{\!\:10^5\!\:}\!\right) \!+\!\frac{2\!\cdot\!4}{\!\:3\!\cdot\!5\!\:} \left(\!\frac{144}{\!\:10^5\!\:}\!\right)^2\!\!\!+\!\cdots \!\right\}}\) |
|||
| を得てから円周率を計算した. 貞治は, このオイラーの手法に関して, 10の冪を分母に含めた点に「實用整數論」的手腕を認めている.「一寸眞似の出來ない藝當で, アルキメデスの再生とも言うべき所」と賞讃する (p.90) のである. 数学史上における円周率の計算技法の向上に関しては, 現代では既に数多の解説書が出版されているが, これが人口に膾炙していなかった時代にあって,『數學の自由性』は多くの読者の興味を掻き立てたことと想像される. 周知の通り, 現在でも小数点以下の桁数の記録は日々更新され続けている. コンピューターの機能性を図る指標とされることもあるが, 如何に収束スピードの速い級数を得るかが本質的な重要性をもつと言えよう. ラマヌジャン (Srinivasa Ramanujan, 1887-1920) が考案した円周率に関する数々の驚異的な公式は現代ではよく知られている. 直近では, 高速で収束するアルゴリズム (チュドノフスキー法による級数) |
|||
| \(\displaystyle{\frac{1}{\!\:\pi\!\:}=12 \sum_{k\!\:=0}^{\infty} {\frac{(-1)^k (6k)!\,(545140134\!\:k+\!13591409)}{(3k)!\,(k\!\:!)^3(640320)^{3k + 3/2}}}}\) |
|||
| を用いて202兆桁まで計算されているという (2024年6月28日現在. 米国の Wikipedia による). 閑話休題. 現在,『數學の自由性』は絶版であるが, 現代仮名遣いに改められた |
|||
| 『数学の自由性』筑摩書房 (ちくま学生文庫), 2010, 全346頁. | |||
 『数学の自由性』(ちくま学芸文庫, 2010) |
|||
| は入手しやすい. この [学芸文庫版] には, 前出の『過渡期の数学』,『中学時代のこと』,『明治の先がた』,『オイレル方陣について』のみならず,『訓練上数学の価値』(1936),『現代数学の抽象的性格について』など, 貞治の数学思想が現れた小篇がいくつも収録されている. |
|||
| §6.教え子達の追想から | |||
| §6-1. 貞治への評価 | |||
| 本稿冒頭部において, 私が本稿を執筆する動機に関して簡単に述べた. 前掲書 [本田] (『高木貞治の生涯』(日本評論社『数学セミナー』1975年1~6月号) を執筆した本田欣哉 (1924-2018) は, これに関して次のように述べている. |
|||
| 高木博士という人物は, 偉人ぶらず, 天才ぶらない点で, 終始一貫している. 84年の生涯を, '普通の人' として生きた (中略). 何の劇的波瀾も無く, 普通の人として坦々と生きながら, しかしその生涯のある時期に, 渾身の力をふるってひとつの masterpiece を生み出し, そしてふたたび, 坦々とした後半生を生きた. 博士の生涯には, 玄妙で豊かな味わいと, ひとつの美があり, それは数学者だけでなく, 一般の人々にも十分味わってもらうことができる (後略) . |
|||
| 同様の記載は,『高木先生の伝記』(前掲書 [追想高木] p.182) にも見られる. 貞治は,『わたしの好きな數學史』(前掲) において「正確なる史實の記錄」を挙げた. とは言え, 本人でさえ,「正確」を期すことは容易ではない. 貞治自身, 先に引用した『中学時代について』のほか, 他の箇所でも |
|||
| 過ぎ去ったことを正確に伝えるのは, 非常に難しい.『一数学者の回想』 回顧は老人の追想談になるのが普通で, それは通例不確かなものである『回顧と展望』 |
|||
| などと述べている (何れも冒頭部で言及されている). [本田] は, 直接的に貞治を知る多くの人物を取材し, 多くの記録を調査した労作であるが, 取材対象が (記事記録ではなく) 人間である場合, 上記の「記憶の不正確さ」は, 当然考慮されなければならない. 例えば, 幼少時代の貞治の神童ぶりを伝える『岐阜日日新聞』(1886年1月7日付) による「記事」として, [本田] には |
|||
| 美濃国本巣郡数屋村高木勘助の長男貞治というは今年漸く10年1ヵ月と成り, まだ乳臭を離れざるも, 夙に一色小学校に通学し, 当時既に高等三級の学課を修め, 頗る穎才の天資なるに, 加ふるに映雪聚螢の勉励と師父教育の懇切にして, 大いに学業勇進し, 正科の外に更に英学を研究し, 愈よ奮発し怠らざるよし, 実に後世頼もしき神童なりと. | |||
| とある (『数学セミナー』日本評論社, 1975年1月号, p.16). 私はその原典『岐阜日日新聞』を確認していないが, このような公的な「記事」に関しては, 誤謬は少ないと考えられる. 尤も, 引用者側にミスが生じることはあり得る. 上記引用部には一部に旧字や旧仮名遣いが見られる (恐らく修正洩れであろう) が, 当時の新聞は全般に亘って旧字および旧仮名遣いで表記されていたことと思われる. 一方, 大学時代の貞治の秀才ぶりを伝える八田三喜 (1873-1962) による「伝聞」として, [本田] には |
|||
| 微積分の試験の前に, 本多光太郎 (後年, 鋼鉄の研究で文化勲章を受賞) が友だちに向かって,「俺はノートを4へんよんだから, どこから出てもいい」というと,
高木が皮肉な微笑を浮かべて,「数学って, 暗記する学問ですかね」といった. ガムシャラに勉強する本多の善良性へのこの皮肉は, 高木の現代人的な知的な性格を,
鮮明に示しているのである. ところで, この藤沢の試験の結果であるが, 高木の成績は140点であった. もちろん, 100点満点なのである. この点数は, 高木の数学的頭脳の冴えを示すとともに, その冴えを敏感にキャッチして, かつそれを独特の流儀で表現した, 藤沢の頭脳と性格をも示しているのである. |
|||
| とある (『数学セミナー』日本評論社, 1975年2月号, p.34).「受賞」なる記載がミスであることは直ぐに気づくが, 八田三喜の記憶までは検証できない. 藤沢か本多または貞治自身の述懐があれば話は別であるが,
私自身はこれに関する他の文献を寡聞にして知らないのである. 本田が八田からこの逸話を聞いたのがいつであったかは記載されていないが,「高木と大学時代のはじめ同級であった八田三喜氏と, 筆者はその生前インターヴィューをすることができた. (その後, 昭和37年, 89歳でなくなった.)」と記載されている. 従って, この記事が『数学セミナー』に発表された時点では, 誰もこの逸話を検証できない状態にあったわけである. なお, 本田自身はこの逸話がお気に入りであったようで,『100人の数学者』(数学セミナー増刊, 日本評論社, 1989, p.178) や『高木貞治の生涯』(『数学セミナー』日本評論社, 2010年3月号, p.10) でも (各々異なる私見を交えながら) 紹介している. 伝記ないし評伝を書く際には, 多くの困難を伴う. これは, 筆者が特定の人物に興味関心をもつがゆえに執筆されることが多い. その場合, 多かれ少なかれ, そこには筆者の感情 (畏敬や崇拝, 憧憬や憐憫, ときには軽蔑や嫉妬など) が含まれることになるであろう. 人物を評価する場合, 過小評価することは無論避けるべきであるが, 過大評価することも避けるべきであろう. 性格や業績に見解を挟む場合にも, 矛盾が生じないよう, 注意を払う必要がある. 本田は, 貞治を「偉人ぶらず, 天才ぶらない (中略) 普通の人」と評する一方で, 上記の例を引いて「本多の善良性へのこの皮肉は, 高木の現代人的な知的な性格を, 鮮明に示している」と評している. 前者の評価については, 特に異論はない. 後者の評価おける「善良性への皮肉」なる表現が気に掛かる. 本多の言う「ノートを4へん読んだから」云々は,「試験範囲における数学を丸暗記した, または当該箇所の論理の要点を完全に理解した」の意味であろう. 貞治は,「数学は暗記によって理解する (し得る) とする考え方や姿勢」を穏やかに批判したのであろう.「ガムシャラに勉強する本多の善良性」とは, 何事に対しても成り振り構わず懸命に努力する本多の性格を指すものであろうか. 貞治は, 本多のそのような部分を,「皮肉」ったのであろうか. この点に些か疑問が残るのである. さらに,「この皮肉」が「現代人的な知的な性格を (示し)」なる表現も気に掛かる. これを読む限りでは, 具体的に如何なる状態を指すものかが判然としない. 具体性のない「何か」をもって貞治を無意識の裡に過大評価する仕儀に陥っていないであろうか. 「100点満点」中, 如何なる理由で「140点」であったかに関して八田の言明はなかったにも拘らず (あったならばこれも記載すべきであろう),「高木の数学的頭脳の冴え」あるいは「独特の流儀で表現した, 藤沢の頭脳と性格」云々に関しても, やや憶測が過ぎるように思う. 仮に, 貞治がこれを読んだとしたら, 何と述べるであろうか. 私自身は,「高木の成績は140点」なる逸話に関しても貞治ならば「それは正確ではない」と否定するかも知れない, などと憶測する者である. |
|||
| 一方, 河田敬義は, この種の逸話の取り扱いには慎重な姿勢を見せている. [追想高木] 所収の『追悼会での思い出ばなし』(pp.207-210) では, 貞治が逝去した翌年に開催された内輪の追悼会の席上で遺族や関係者から語られたことが記されている. ただし,「録音したのではないから, 不完全なものであり, 聞き誤りもあったかも知れない. また, 多くの方々はすでに亡くなられたので, 確かめることもできないままである.」とある. 河田敬義の誠実さが伝わる文章である. ちなみに, 河田自身の人となりについては, §4-9.における前掲書『柔らかい頭と強腕 河田敬義追想集』(1994) に詳しい. 因みに, この『思い出ばなし』には, 末綱恕一や守屋美賀雄 (1906-1982), 菅原正夫や黒田成勝などの教え子達による |
|||
| 末綱 Klassenkörper を類体と訳されたのは高木先生であった. 私は共立社の講座を書くときに級体としたが, 先生の気に入らなかった. これは後の類数 (Klassenzahl) という訳とも関連していた. | |||
| 守屋 Bewertung を賦値と訳したのも先生であった. | |||
| 菅原 大学を卒業したとき, 先生から数学が分かったかと言われて返事に困った. いくらか分かったような気がすると答えたら, 先生はそれは嘘だ, もっと具体的な問題からやり直せと (後略) | |||
| 黒田 ブロウエルの論文を読んで, 初めの集合の定義が分からなくて, そう言ったら, 先生もよく分からないと言われたことがあった. | |||
| などの回想が語られている. また, 貞治の類体論を最も理解している門下生の一人である彌永昌吉は, 貞治の「ガウス数体の上の相対アーベル体がすべてルジャンドルの楕円関数の特殊値で生成せられる」ことを示した学位論文を紹介する文脈において, |
|||
| 後の御仕事をも合せ考えれば, 先生はこの時すでに一般相対アーベル体の理論について重大な予想を持っておられたのではないかと想像される. 然るに先生はその後約10年間,
一つも論文を出されなかった. (中略) 先生は先生としての夢を育みつつ, 徐ろに想の熟するのを待たれたのであろう. (中略) あくせくと仕事をし, 焦り気味に発表する多くの学者とは, 全く正反対の行き方である. 先生の落着いた, 自ら深く信ずるところのある, 迫らない御性格によってのみ, 始めてこのようなことができたのである. |
|||
| と記したことがあった (前掲書 (§3-7.) [彌永8], pp.8-9). この記事の初出は1940年11月発行の『帝大新聞』であり, この文章は恐らく貞治の目にも止まったのであろう. その直後 (1940年12月7日) に開催された講演『回顧と展望』において,「類体論は主として第一次世界大戦の「刺戟」によって始められたので, そう前から考えていたのではない, と述べられた」ことを受け, 彌永は次のように追記した (同書, pp.11-12). |
|||
| 勝手な想像で書いたりしたことを, 申し訳なく思った (中略). これが, 先生を冒瀆することにならねばよいが, と私は気遣っている. ただ心中いつも先生に頼っている一人の書いたもののこととて, わりなきふしもあらば, と御諒恕あらんことを, 先生および読者にお願いするのである. | |||
| 彌永は貞治を尊敬するあまり, 理想化した憶測を加えてしまったのであり, 他意があったわけではない. それを理解しつつ, それでも自身に対する過大評価を看過できない貞治は, 講演においてその憶測を修正したのであった.「偉人ぶらず, 天才ぶらない」というよりも, 事実を正しく認識し, また認識してもらおうとする貞治の科学者的な姿勢が, このようなところに如実に現れていると言えよう. 一方, 上記のように自身の誤りを詫びる彌永に見られる謙虚な姿勢にも感心させられる. 些細なことながら, 上記『回顧と展望』の講演日を「12月7日」と記したのは,『近世數學史談』第2版 (1942) の記載によるものである. 第3版 (1971) や直近の岩波文庫版 (1995) に至るまで, この日付に異同はない. 一方, 初出の『高數硏究』(§2.に紹介した [速記版]) には, その前日「12月6日」なる記載が見られる. ところで, 過大評価されることを好まなかった貞治は, 過小評価されることに関しては如何なる判断を下したであろうか. 「高木関数」を知らなかったランダウがファン・デル・ヴェルデン (Bartel Leendert van der Waerden, 1903-1996) の構成した関数を高く評価した件 (§4-9.) について, 貞治が何か批判した様子はない. 後年,『解析概論』の当該箇所では, 淡々と事実を述べたのみであった (p.471). ランダウにとって, 相手が貞治であったことが幸いした. これがルジャンドルやコーシーであったら, ランダウは彼らに罵詈雑言を浴びせられたことであろう. 類体論の概要を発表した時点では, 貞治の理論は誰にも理解されず, 何の反応もなかった. これも一種の (主体性の無い) 過小評価と言えようが, これに関しても貞治がどこかで不満を洩らした形跡はない. 時が熟するのを待って, ジーゲルおよびアルティンに論文を送付したのみであった. |
|||
| §6-2. ビ分のことはビ分でせよ | |||
| 他にも, (故意ではないが) 貞治に対する過小評価に繋がった実例がある. 私が最初にこの実例を知ったのは, |
|||
| [梅田1] 梅田亨『「微分のことは微分でせよ」とは』/ 日本評論社『数学セミナー』2004年1~3月号. | |||
| によってであった. これは後に単行本化され, | |||
| [梅田2]『徹底入門 解析学』日本評論社, 2017, pp.2-23. | |||
| に収録された. 以下に述べることの要点は, 全てこの著作に掲載されている. 但し, (上述した理由で) 孫引きを避けるため, 私自身が確認できた範囲のものをここに記すことにする. 私が矢野健太郎 (1912-1993) の名を知ったのは, その著書 |
|||
| [矢野1]『数学のたのしさ』新潮文庫, 1976, 全237頁. | |||
|
を読んだ中学3年生時のことであった (拙稿『楽しい読書・夏』(2009) 参照). 矢野には, 論文 (微分幾何学関連) の他に, 大学生用の数学演習書や高校生向けの受験参考書, 一般人向けの啓蒙書など,
夥しい数の著作があることはよく知られていよう. 矢野は1931年に東京帝大に入学し, 1934年に卒業した. その後2年間, 1936年までを大学院生として過ごした. 貞治の代数学の講義を学部時代に聴講している. 貞治が定年退官したのが1936年の3月であるから, 貞治の教えを受けた学生としては最年少の世代に属する. |
|||
| [矢野2]『ゆかいな数学者たち』新潮文庫, 1981, 全293頁. | |||
| には国内外の数学者の興味深いエピソードが多数紹介されており, 貞治に関する逸話も10種類ほど掲載されている (pp.16-28). 代表的な逸話は, | |||
| [矢野3]『数学の散歩道』新潮社, 1972, pp.47-49. | |||
| [矢野4]『数学者のおくりもの』旺文社文庫, 1980, pp.268-269. | |||
| [矢野5]『数学者おぼえ書き』新潮社, 1980, pp.21-23. | |||
| [矢野6]『草履を拾っていただいた話』前掲書 [追想高木] , pp.128-131. | |||
| などにも現れる. これらは一字一句同一ではないが, 大意については大同小異であるから, ここでは, 最も簡潔に纏められている | |||
| [矢野7]『東大で教えていただいた先生方の逸話』学士会アーカイブス, No.742, 1979. | |||
| から抜粋する. |
|||
| あるとき高木先生は, この雑誌に1つの論文を寄稿された. それは, いままでは, 微分学の定理であるのに, 積分学を用いて証明されていた定理に対して,
微分学の範囲内での証明を与えられたものであった. そして先生はこの論文を, つぎの言葉で結ばれた.「昔から言うではありませんか. 微分のことは微分でせよと」 |
|||
| この最後の駄洒落は有名である (本稿においては, 前出の『微積の體系といつたようなこと』(以下 [體系] と略記する) の項で引用済みである). 私のこれまでの勤務校においても, 年配の教員が, 微分に関する問題を質問しに来た生徒に対して (冗談としてではあるが) この駄洒落を発するのを何度か耳にしている. 但し, 私がこれを知ったのは [體系] によってではない. 高校生時代あるいは大学生時代に読んだ [矢野5] によってこれを知った. 単なる駄洒落として記憶されただけではない. 貞治が何か独創的な発想をもって画期的な証明を発表したらしいことも, 鮮明に私自身の記憶に残されたのである. 私が『數學の自由性』を繙いたのは [梅田1] を読んだ後のことである. 梅田の報告に驚愕し, それを確認するために初めて『數學の自由性』を手にしたのであった. ところで, これを孫引き (曾孫引き?) したと思われるのが, §4-9. の項で私が「名著」の一つとして掲げた |
|||
| [赤1] 赤摂也『微分学+積分学』数学セミナーリーディングス, 日本評論社, 1973, 全224頁. | |||
| である. その「まえがき」は, |
|||
| 本書は題して〈微分学積分学〉という. その内容は, 通常,〈微分積分学〉ないしはつづめて〈微積分学〉とよばれるものである. | |||
| なる書き出して始まる. これ自体は, [體系] において貞治が言及したものと同等の名称に関する話題であり, 特に問題はない. ところが, その後半には, |
|||
| 〈微分学〉を〈積分学〉から全く分離し,〈微分学積分学〉と題したのも, 一にこの分野の理論構造をよりあきらかにしようと思ったからにほかならない.〈ビブンのことはビブンでせよ〉というのは高木貞治先生の名警句であるが, 私は, これを進んでそっくり頂くことにしたのである. | |||
| と記されているのである. これが, 貞治の意図と真逆であることは, [體系] を読めば明白であろう. そもそも, この句が「警句」として発せられたものではないことも [體系] を読めば分かるはずであるから, 赤自身はこれを読んでいない可能性が高い. であるならば, 赤の文言は, [梅田] p.2 にあるように「引用の孫引き・曾孫引き」ということになる. |
|||
| 出版年月から見て, 引用元の可能性があるのは, (§4-9. の項でやはり私が「名著」の一つとして掲げた) 一松信『解析学序説 上・下』(裳華房, 1962-1963) 即ち | |||
| [一松1] 『解析学序説 上』裳華房, 1962, 全342頁. | |||
| [一松2] 『解析学序説 下』裳華房, 1963, 全316頁. | |||
| [一松3] 『解析学序説 上 (新版)』裳華房, 1981, 全275頁. | |||
| であるか, または [矢野3] であろう. [一松1] における該当箇所 (第Ⅱ章 積分法) には,「基本定理」即ち「連続函数は必ず原始函数をもつ. 原始函数は, 定義域内の一点での値を定めれば, 一意的に定まる.」の証明に関して, |
|||
| この定理はみかけ上は, 微分方の域に属するものであるが, 普通は積分 (定積分) を作って, それがちょうどうまく原始函数になっている, ことを証明する. (中略) 定積分の概念に依存せず, 微分法の範囲内だけで証明することも, まったく不可能ではない.*) しかしそれにはかえって不自然な技巧が必要なので, ここには採用しない. | |||
| とあり, 脚注*) を見ると, | |||
| かつて高木貞治先生が 'ビブンのことはビブンでせよ' という有名なシャレをとばしたものである. (数学の自由性, 考え方研究社, 1949, p.32; 同所に書かれた高木先生の意見には含蓄が多い.) | |||
| とある (pp.48-49).「ビ分」(貞治) でも「微分」(矢野) でもなく,「ビブン」(一松) と表記した点から見て, 赤による引用部は, 一松の上掲書からの曾孫引きである可能性が高い.
また, [一松2] における当該箇所「第X章 一様収束」を見ると,「定理10.7. (項別微分の定理)」に対する (\(\{f_n(x)\}\,\)の各点収束性と\(\,\{{f_n}^{\!\prime}(x)\}\,\)の一様収束性による) 証明が示された後に,「別証」が掲載されている. そこには, |
|||
| 定理10.7 は文面上は微分法の定理であるから, 積分を使わない直接証明を与える.*) | |||
| とあり, \({f_n}^{\!\prime}(x)\,\)の連続性や可積分性を仮定しない証明が示されている. 脚注*) を見ると, | |||
| このような証明は, 単に sectionalism 的な 'ビブンのことはビブンでせよ', という興味だけではない. 定理自身の精密化, および後述のようにこれによって基本定理の一つの証明ができる点が重要なのである. | |||
| とあり, [體系] において貞治が紹介したシュミットの方法が「補題10.8. 基本定理 (連続函数は原始函数をもつ)」の証明中に紹介されている (pp.52-54).
一松が [體系] を読んでいることは疑いがない. 上記引用箇所に見られる "sectionalism" が単行本『數學の自由性』で追記された台詞であることは, 前節 (§5-6.) において述べた通りである. 次に, これらの著作の改訂版である [一松3] を見てみよう. 配列や表記における (旧版に対する) 大幅な変更は, 恰も別の著作に見えるようなレヴェルの改訂である. 旧版では一変数と多変数で上巻と下巻に分別されていたが, 新版では実用的な話題と理論的な話題とで上巻と下巻に分別されたのであった. 余談ながら, 私自身は旧版の方を好んで読む者である. さて, 当該箇所「7. 級数・整級数」を見ると,「定理7.18. (実変数の項別微分の定理)」の証明の後の「注意」として, |
|||
| 定理7.18 は, 形の上では微分法の定理であり, 積分を使わずに証明することも可能だが面倒である. 高木貞治先生の有名な言葉 'ビブンのことはビブンでせよ' は, 元来この定理に対するものであった. | |||
| と記載されている (p.192). 旧版では,「割拠主義をもって定理の精密化と基本定理の証明の一つが得られる点が重要」と述べた一松が, 新版では「積分を用いない証明は可能だが面倒」と片づけてしまっている. 因みに, |
|||
| [一松4] 『解析学序説 下 (新版)』裳華房, 1982, 全286頁. | |||
| には, この話題に関する記載は一切見られない. |
|||
| [梅田] においては, 矢野の事実誤認が厳しく責められる. 即ち, この駄洒落が発せられたのは, 論文においてではなく, 結びの文句でもない, 抑々この「新証明」自体が貞治の考案によるものではない,
等々. 矢野自身は, 後に単行本化された『數學の自由性』ではなく, この話題の初出である『高數硏究』における [體系] を読んだものと思われる.『數學の自由性』には「微分, 積分」の名称および「初学者へ微分積分を手引きする手段」に関する貞治の見解が追記されていることは既に述べた. 矢野の記述法を見る限りでは, 矢野はこの追記部分を読んでいないか, または, 駄洒落に気を取られるあまり (本質的な重要性を見落として) 失念してしまったかであろう. 元来, [矢野1] から [矢野6] までの一連の著作は, 数学を専門としない一般読者を対象として執筆されたものである. 一般的には, 堅苦しく気難しい性格をもつ別世界の存在と看做されている「数学者」を, ユーモアのある親しみ易い存在として紹介しようとした矢野の意向は充分に理解できる. しかし, とは言え, 人物の過小評価に繋がる事実誤認を看過するわけにはいかないであろう. 事実, これを受けての『微分学+積分学』「まえがき」における曾孫引きである. 原典を照合せずに貞治の一部の台詞のみを切り取って掲載した矢野および赤の責任は大きい (照合した上での誤解, 表記ミスの可能性もゼロではないが……). また, 原典を熟知していたと思われる一松による上記のような脚注も, やはり誤解を与えかねず, 全く責任がないとは言えないであろう. その結果, [梅田] (p.3) にある通り, |
|||
| これらの引用文を見ると, 高木貞治は, (1) 微分学の定理はできるなら, 微分学だけで証明するのが望ましい (2) 或る微分学の定理に対し, 微分だけ使う証明を自ら工夫した, ように見える. 上の引用は, もちろんこれを肯定的にとらえているが, 陰では逆に「高木貞治は解析学者でなく, 代数学者だからそんなセンスの悪いことをやったのだ」というアンチ高木の評価をしたり顔で述べる人もいる. |
|||
| となるわけである. 最後に言及される「したり顔で述べる人」が誰を指すものかは不明であるが, SNS 上における匿名の何某を指すものであれば,
私自身も該当者 (該当記載) を見かけたことがある. |
|||
 梅田亨『徹底入門 解析学』(日本評論社, 2017) |
|||
| これが貞治に対する過小評価の例である. これに関する貞治への誤解が拡散しないよう, [梅田] が人口に膾炙することを望みたい. 余談ながら, [梅田] は,「有界収束定理」および「フーリエ級数」に関する独自の視点による解説が収録された, 大変に興味深い著作である. また, 上記のような瑕疵は見られるものの, 赤摂也の『微分学+積分学』も, 他にあまり類を見ない特異な構成法をもつ, しかし厳密且つ明快に書かれた名著であるという評価に変わりはない. 私自身が長年所属している数学研究サークル (各月開催) においても, 赤摂也による数学書は概して評判が良い. このサークルでは, 嘗て, |
|||
| [赤2] 赤摂也『集合論入門』培風館, 1957, 全180頁. [赤3] 赤摂也『確率論入門』培風館, 1958, 全224頁. |
|||
| を, 各々, 一年ほどの期間をもって講読したことがあった. いずれも, 省略や誤魔化しのない厳密かつ単純明快な論理構成に感心させられた著作である. 矢野にせよ, 赤にせよ, 原典を確認せずに貞治の台詞の一部のみを切り取って掲載したことは問題であったが, 根柢には彼らの貞治に対する畏敬の念が窺えるものであった. 記憶違いや多少の憶測が含まれることを前提して読むならば, 矢野による貞治に関する逸話は (他の数学者に関する逸話も含めて), 大変に面白い. 次の「NとO」に関する逸話も同様である. 再び [矢野7] から引用する. |
|||
| 私より2年後輩の田島一郎君が「高数研究」という雑誌の編集をしていた. 高木先生は田島君から求められて, ときどきこの雑誌に面白い記事を寄稿された.
それらの一連の記事は, Nという人物とOという人物の対話の形をしていたが, Nが愚問を発すると, Oがそれをたしなめつつ, 詳しい数学的な説明を与えるという形をしていた. 田島君も私も, このNとOは何を意味するかわからなかったが, 恐る恐る高木先生に伺ったところ, このNは NANJI (汝) の頭文字で, Oは ORE (俺) の頭文字であるという先生のお答えであった. |
|||
| 『高數硏究』に現れる「O」と「N」については先述した (§5-6).「Nが愚問を発する」なる表現が適切かどうかはともかく, 先述した通り,「O」と「N」の間には, 読んでいて小気味よい「落語を聴くかのような丁々発矢の遣り取り」が交わされるのである. それらは全て, 貞治の優れた表現力の賜物にほかならない. 矢野は, この逸話に関しても他の複数の著書で紹介している. 上記の引用部を見る限りでは,「恐る恐る高木先生に伺った」のが誰なのかは不明であるが, [矢野2] によれば, 田島が貞治に尋ねたようである (pp.23-24). |
|||
| あるとき田島君が,「矢野さんは先生の文章に出てくるNという名前をOという名前のいわれを知っていますか」と聞くので,「そんなことは僕には判らないよ.
高木先生に直接伺ってみたらいいだろう」と答えると, 田島君は,「そんなこと先生に聞いてもいいかな」と言っていたが, 思い切って先生に伺って,
しばらくすると私につぎのように教えてくれた. 「矢野さん. 判ったよ. 高木先生に伺ったところ, Nは NANJI (汝), Oは ORE (俺) の頭文字だってさ」なるほど, おかしなことを言うのは汝であって, これをたしなめるのは俺というわけであった. |
|||
| 一方, 矢野の『草履を拾っていただいた話』([追想高木] p.130) には,「私はこのNとOの意味がよく判らなかったので田島君にきいてみた. ところが田島君も知らないという.」とある. 田島から発せられた疑問なのか, 矢野から発せられた疑問なのか, という点に関して, 両者の記載内容には矛盾が生じている. 些細なことであるが, 矢野の複数の著作には, 同一の逸話であってもこの程度の差異 (少なくとも一方は事実と異なる記事) が見受けられるのである. 『高數硏究』にたびたび原稿を依頼していた田島がNとOの謂われに関して尋ねたのだとすれば, 田島自身も何かの折にこの話題に触れていそうなものである. しかし, 彼の著作は, (私が知る限り) 純粋な数学書 (『解析入門』(岩波全書),『イプシロン-デルタ』あるいは『整数』(何れも共立出版, 数学ワンポイント双書) など) のみであり, この逸話に触れた田島の随筆ないし評論を見かけたことはない. とは言え, この逸話が矢野自身の創作 (想像) のみで書かれたわけではないであろう. 上掲した [矢野1] から [矢野7] が出版 (発表) された時点では, 田島はまだ存命であったからである. |
|||
| 貞治とは直接の関連性はないが, 矢野の著書に見られる事実誤認と思しき他の実例について触れておく. |
|||
| [矢野8]『数学者おしゃべり帳』新潮社, 1982, pp.124-125. | |||
| には [矢野2] の「こぼれ話」として数名の学者達の逸話が掲載されている. その中に次のような逸話がある. |
|||
| 若いK教授の話である. K教授は終戦後いち早くアメリカに渡り, アメリカで数々の立派な業績をあげた方であるが, 日本のある大学から要請されて帰国され, その大学の学生を指導することになった. ところがちょうどその時期に, 理学部長の改選が行なわれることになった. K教授のように研究一途の方が理学部長に向いているかどうかについては私には何とも言えないが, それでも選挙となれば, 立派な業績をあげて帰国されたK教授に票が集まりそうな形勢になった. ところが, どこからか,「理学部長に専門馬鹿は困りますね」という妙な言葉がきこえてきた. これを聞いたK教授は, 思わず,「専門馬鹿でない人はただの馬鹿ですか」と反問して動じる色はなかったという. |
|||
| 矢野の著作に見られる各学者の逸話に関しては, 出典が明記されていない. 矢野自身が直接見聞きしたか, あるいは噂ないし伝聞として耳にしたものを, 記憶を頼りに執筆しているように思われる. 上記のK教授が誰を指すものかは [矢野8] を読む限りでは判らないが, 小平邦彦 (1915-1997) であることは明白であろう. 小平は, その著書 |
|||
| [小平]『ボクは算数しか出来なかった ―― 私の履歴書』日経サイエンス社, 1987, 全181頁. | |||
| において次のように回想している (pp.152-153). |
|||
| 昭和42年 (1967年) の8月半ばに日本に帰って, 東京大学の数学教室に復帰した. (中略) 翌43年の夏に東大紛争が始まった. (中略) しばしば団交が行われて, 教授達が学生に専門バカと罵倒された. ある日, 紛争に対する理学部の意見をまとめるからめいめい意見を書け, という回覧板が回って来たので, 私は「専門バカでないものは唯のバカである」と書いて出した. そうしたら, この句がそのまま理学部の意見の中に採用されて有名になった. 3年後の昭和46年の11月4日の教授会での選挙で, 私は理学部長に選出された. 怠けものの私はあまり教授会に出席せず, この日もうちにいたら選出されたという電話があった. ギョッとした. アメリカから帰ったばかりで, 日本の習慣もまだよくわからず, 評議員はおろか教室主任もしたことがない私に学部長が務まるとは思えなかったし, 東大に帰るとき雑用はいっさいしなくてよいという約束があったはずであるから, 断ろうと思ったが, 断った先例がないということでついに学部長にさせられてしまった. |
|||
| ここにおける矢野および小平の記載事項は齟齬を来している. 何れか一方, または両者共々による記憶違い (事実誤認) があるものと思われる. 小平に関する逸話であるから, 小平自身の記憶違いの可能性は (矢野よりは) 低い. 少なくとも, 小平自身に学部長就任を望んだ気配はない. 周囲の者達が小平の意思に反して学部長に仕立て上げたわけである. であるならば, 矢野の言う「どこからか,「理学部長に専門馬鹿は困りますね」という妙な言葉がきこえてきた. これを聞いたK教授は……」の話は, 事実ではないことになる. 小平が「専門馬鹿でないものは」云々を発したのは教授会においてではないからである. 矢野は, 恐らく, 小平のこの台詞をどこかで聞きかじったものと思われる. 選挙で学部長に選ばれた話も知人から聞き知ったのであろう (当時の矢野は東工大の教授であり, 東大には所属していなかった). この二つを結び付けて話を面白くするために,「どこからか」,「妙な」などという曖昧な表現を付随させてこの逸話を仕立て上げた可能性が高い. 尤も, このような作り話を知人から耳にした矢野が, そのまま横流しした可能性もないとは言えない. |
|||
 小平邦彦 (1915-1997) |
 『ボクは算数しか出来なかった』 (日経サイエンス社, 1987) |
||
| [小平] の原稿が日経新聞に掲載され始めたのは1986年であるから, これを執筆した時点で小平は [矢野8] を読んでいた可能性がある. 無論, 矢野にも同様のことが言える. 但し, 矢野も小平も互いに相手の著書に関しては何も言及していないので, 何れの逸話が事実かに関しては, 我々部外者には判断しかねる. 因みに, 東大の理学部長としての小平邦彦の前任者は久保亮五 (1920-1995) であった. これも矢野の言う「若いK教授」に該当するが, 久保が渡米したのは1963年であり,「終戦後いち早くアメリカに渡」ってはいない. 一方, 小平のプリンストン行きは1949年であるから,「終戦後いち早くアメリカに渡」っている. [小平] では,「プリンストン行き」の章で, 貞治との関わりが紹介される (p.83). |
|||
| プリンストンの高級研究所の所員には全然義務がなく, 自分の好きな研究をしていればよい, という話を聞いて, (中略) 行けたら, さぞうれしいだろう,
とは思ったが, 怠けものの私はこちらから願書を出す, などということには全く思い至らなかった. 昭和23年の春, 菅原正夫先生から,「高級研究所のワイル教授に君の推薦状を書くように高木貞治先生にお願いしておいたから」という話があった. それから半年ほど経ってワイル教授から, 1949年 (昭和24年)9月から一年間高級研究所に来ないか, という招待状がきた. 早速, 菅原先生と一緒に高木先生のお宅にお礼に行ったら, 高木先生は悠然として「エヘヘ……実は怠けていてまだ何も書いてないんで……」と言われた. なるほど, 大先生というものはこういうふうに悠然としているものか, と感心した. |
|||
| 同様の記事は [追想高木] pp.162-163 にもある (両者の原稿の執筆時期は, ほぼ重なっている). 貞治が小平の推薦状を書かなかったとしても, 何かの折に直接または伝言をもって小平の件をワイルに伝えた可能性はある. 仮に貞治が全く動かなかったとするならば, 純粋に数物理学上の業績をもってプリンストン招聘を実現させた小平の実力は見事というほかはない. [追想高木] では, 上記の逸話に続けて, 学士院賞受賞の際の貞治に関して |
|||
| 昭和32年の春, 高木先生から「学士院賞を貰っていただきたく, ついては論文の別刷を送っていただきたく……」という手紙を戴いた. (中略)
面倒かも知れないが我慢して別刷を送って学士院賞なるものを受賞してほしい, という調子の文面で, 受賞が決ってお目出度うなどということは書いていなかった,
と記憶している. 日本に帰って学士院会員になってみて, 数学の業績に学士院賞を出すには, その業績が賞に値する重要なものであることを第ニ部の多数の会員が納得するように説明しなければならず, それが非常に難しいことを知り, 当時82歳の高木先生が私のために大変な苦労をして下さったことに感謝の念を新たにしている次第である. |
|||
| と回想されている (pp.163). 余談であるが, [小平] (p.129) には後日談が載っている. 貞治から上記の手紙を受け取った小平には, 授賞式に出席せよという通知は来なかったようである. その「通知は東京の留守宅の母の所で止まってしまったらしい. 授賞式には母が代わりに出席したと後で聞いた.」 |
|||
| [矢野2] に掲載された数学者達や物理学者達の逸話は, (多少の脚色はあるにせよ) 面白いものが多い. 脚色を疑えば際限がないが, その件は保留にして,
貞治自身の言及が存在する例を紹介しよう. 矢野はまず, ドイツ留学から帰国したての新進気鋭教授であった貞治が集合論の講義で学生に説明したことを紹介する. \(\mathbb{N}\,\)のような可付番 (abzählbar) 集合の濃度を\(\,\mathfrak{a}\), \(\mathbb{R}\,\)のような連続 (continuum) 体の濃度を\(\,\mathfrak{c}\,\)で表せば, \(\mathfrak{a}\!<\!\mathfrak{c}\,\)である. その後, 矢野は次のように続ける. |
|||
| 高木先生は,「濃度\(\,\mathfrak{a}\,\)より大きく, 濃度\(\,\mathfrak{c}\,\)より小さい濃度をもつ無限集合は存在するか, という問題は連続体の問題とよばれるが, この問題はまだ解決されていない」と言ってこの講義をしめくくられた. 先生が教室を出ようとすると「ハイ」と言って手を挙げた学生がいた. 先生が何だねと尋ねると, その学生は「先生がいま言われた連続体の問題解けました」と答えた. 先生が, ほうどんな具合にときき返したところ, その学生は「\(\mathfrak{a}\,\)と\(\,\mathfrak{c}\,\)の間は\(\,\mathfrak{b}\,\)に決っています」と答えたという. ([矢野2], pp.18-19) | |||
| 一方, これに関する貞治の言及は, |
|||
| [高木掛谷]『高木貞治 掛谷宗一 兩博士縱橫對談記』/ 考へ方研究社『高數硏究』第5卷第8號 (1941年5月), pp.24-35. | |||
| に現れる. この対談全般に亘る貞治と掛谷の遣り取りは大変に面白いが, それらは割愛して, 濃度の関する部分のみを抜粋する. |
|||
| 洒落で面白かつたのは何時か集合論の講義をしてゐた時に, 濃度が\(\,\mathfrak{a}\,\)と\(\,\mathfrak{c}\,\)との間の集合はあるかないか分つて居ないといつて敎室を出たら, 或る學生が黑板の處へ行つて\(\,\mathfrak{a}\,\)と\(\,\mathfrak{c}\,\)との間には\(\,\mathfrak{b}\,\)があるとやつたんだ. (笑聲) この洒落はインターナシヨナルだから記錄にとつておき給へ. (笑聲) 巧い洒落をいつたものだと思つて, 非常に感心した. 保證に半分位判を捺してもいゝんだけれども, 相憎頼みに來ないんだ. (笑聲) それとも誰かに習つて來たのかも判らないね. | |||
| 貞治はこの学生を賞讃して「この洒落はインターナショナル」としているが, 各々の記号が異なる言語の頭文字を採られている (可算濃度を独語で, 連続体濃度をラテン語 (または英語) で表記している) 点が気に掛かる. たしかに, カントール (Georg Cantor, 1845-1918) は "continuum" を用いたが, これはラテン語であって独語 "Kontinuum" ではない. 仮に, 可算濃度の記号にラテン語版 "numerabilis" の頭文字を当てたとしても, この洒落は成立しないし, 可算濃度を\(\,\aleph_0\), 連続体濃度を\(2^{\aleph_0}\,\)または\(\,\aleph_1\,\)で表すこと多い現代にあっては猶更である. その点, 貞治による「ビ分のことはビ分でせよ」, あるいは [矢野2] に掲載された角谷静夫 (1911-2004) による「それはポアソン分布か?」(pp.80-82) の方がセンスが良い (後者は, 数学者間の会話であれば「インターナショナル」として通用するであろう). 上記の学生による洒落は, 貞治が言うように, 当時の学生達あるいは一部の学者達の間では既に言い古された小噺の類であったかも知れない. |
|||
| §6-3. アカデミック・コーター | |||
| [矢野7] ではもう一つ有名な逸話が語られている. |
|||
|
私が在学中の東大数学科の時間割は, 何時から何時までは何と, 1時間きざみで表示されていた. しかし教室から教室への移動などで時間がかかるので,
実際には先生方は, 15分過ぎか20分過ぎに教室へこられた. しかし高木先生は, たとえ先生のお部屋まではきておられても, 必ず30分過ぎに教室へこられて, 30分間講義をして下さった. 私が大学院へ入れてもらって, 少しは先生に心易く口がきけるようになってから私は, 先生にその理由をたずねてみた. すると先生は 「矢野君はアカデミック・コーター (大学の15分) ということを知っているかね」 ときかれた. これは大学の先生はふつう時間より15分は遅れてくる, という意味である. そこで私が聞いたことがありますと申し上げると 「ふつう講義は15分過ぎに始まることになっているのだろう. それにアカデミック・コーターを足すと30分になるよ」というのが先生のお答えであった. なんとも良き時代であったと言わざるを得ない. |
|||
| 大学における貞治の講義が定刻より遅れて開始されることは, 一時的な現象ではなかったらしい. 教え子達達によるこれに関する回想部分のみを [追想高木] から抜粋してみよう ( [ ] 内の数字は, 当人が東京帝大の数学科を卒業した年を表す). |
|||
| 先生はいつも25分過ぎくらいに見えられた. そして内ポケットから小型の手帳を取り出されてから御講義を始められた. (増井真須夫 [1925], p.28) | |||
| 始業時間に15分くらい遅れて講義が始まることが多かったのに, 一時間分の内容を越える充実した講義であった. (吉田耕作 [1931], p.73) | |||
| 一回の講義時間は短くて, 30分か40分だがその内容は充実していた. (倉石治七郎 [1931], p.79) | |||
| 高木先生の講義は必ず30分遅刻して来られたが, 残りの30分で結構内容豊富のものであった. (小松醇郎 [1932], p.87) | |||
| 時間表には午前10時から11時までとなっている講義に, 先生はいつも判で押したようにきっかり10時半に教室に現れ, 先生独特の講義を正味30分で終わり, さっと引き上げて行かれた. (浅野啓三 [1933], p.97) | |||
| 先生の講義は実に理路整然としていて話しに繰り返しがなく, 無駄な言葉がなく, 聞いていて胸のすくような思いがした. だからいつも一定時間きまって遅刻されたにもかかわらず, 講義の進み方が速く内容が充実していた. (村勢一郎 [1934], p.115) | |||
| 先生の御講義は, 規定一時間のところ, 実質30分, その御来場は風の如く迅速であり, 12時の呼鈴と共に御退場も脱兎の如く俊敏である. (北川敏男 [1934], p.121) | |||
| 高木先生の御講義は11時からとあったので, われわれは11時15分までに, 教室へ集って先生をお待ちしていた. ところが, 先生はもうとっくにお部屋まで来ておられるはずなのに, 11時30分までは教室にお見えにならなかった. いつも11時30分になるとはじめて教室へお見えになり, 11時30分に講義をお始めになった. (矢野健太郎 [1934], p.128). | |||
| 彼らの回想によれば, 講義時間が規定より短かったというその講義内容に無駄がなかったのみならず, 教室への入退場の仕方にも無駄がなかったようである. この点は哲学者西田幾多郎の講義と対照的であろう. 余談であるが, 下村寅太郎 (1902-1995) は,『「高木貞治先生の生涯」落穂拾い』([追想高木] pp.258-266) において, 貞治と幾多郎の関わりについて詳しく記している. |
|||
| 高木先生の講義はいつも11時から12時の時間帯で組まれており, 確か週3回であったと記憶している. (中略) 先生は11時からお待ちしているわれわれの処へ, 約20分ぐらい遅れて (中略) それから約40分ぐらい, 先生は考えながら最も簡明で直裁的でしかも最も一般化された独特の思考過程の講義を展開されてゆかれた (後略) (山内正憲 [1935], pp.135-136) | |||
| 教室に11時から12時までのその時間 (ただし先生は20分ぐらいは遅くいらっしたように思うが), 早くから前の方に席を確保して毎度お待ち申し上げたのである. (亀谷俊司 [1936], p.139) | |||
| 当時は講義は50分単位であったが, 学生の集中力は30分が限度というのが先生の持論であったらしく, 毎回きっかり11時半に教室へおいでになり, 12時にはピタッとおやめになった. (栗田稔 [1937], p.144) | |||
| 高木先生の講義は週4回で, 一回の講義は約30分ほどだったが, ゆったりとした話し方で先を急ぐという感じは一度もなかった. (古屋茂 [1938], p.158) | |||
| 時間割のうえでは講義は11時から12時までとなっていたが, 高木先生が数学教室に到着されるのが11時10分頃, それから先生は小使室で悠然とお茶を飲んでおられた. (中略) 講義が始まるのが11時半, 終るのが時間割通り12時きっかりであった. (中略) 講義の内容は先生が当時の岩波講座『数学』に執筆された『解析概論』とほぼ同じであった. 11時半から12時まで正味30分, 週4回で2時間, それで一年間で『解析概論』の終わり (現行本のルベッグ積分は除いて) まで済まされたのだから不思議である. (小平邦彦 [1938], pp.161-162) | |||
| 一回30分余りで, 必ず一つのトピックをすまされるので, 講義をきいた後に, 一種の充実感を味わうことができました. (中略) 全く無駄のない講義で, 知らぬ間にどんどん進んで,『解析概論』の膨大な内容を一年間で殆んどカバーされたのは不思議な程でした. (伊藤清 [1938], p.166) | |||
| 講義には, 高木さんはおそく来て, 時間の半分位しかやりませんでした. (杉村欣次郎 [1912], p.201) | |||
| 先生は11時半頃になると正門の方から大股で坂を下りいきなり教室にはいってこられます. 講義は30分間でしたがどの教授のよりも充実していました. (菅原正夫 [1925], p.222) | |||
| 聞くところによると, 先生は夕食に好物のお酒を召上り, 間もなくおやすみになり夜半に起きて明け方まで数学の研究をなさり, またおやすみになるとのこと, 当然朝寝になり大学に来られる時間が遅れ, したがって講義の時間が短くなるということだったらしい. しかし私達にとっては, 講義の時間が短かかったからまだよかったので, 同じことを二度繰り返されず, 要点だけを押えていかれるので, 内容はずいぶん豊富だった. (正田建次郎 [1925], p.226) | |||
| 貞治が講義の開始時刻を常に定刻より遅らせた理由は何であったか. 上記の引用箇所には,「学生の集中力は30分が限度というのが先生の持論」(栗田), あるいは (毎晩明け方まで研究していたため)「朝寝になり大学に来られる時間が遅れ」(正田) とあるが, 何れも「らしい」という伝聞または憶測によるものである. 後者の「朝寝」は正鵠を逸しているようである.「先生はもうとっくにお部屋まで来ておられるはずなのに, 11時30分までは教室にお見えにならなかった」(矢野), あるいは「高木先生が数学教室に到着されるのが11時10分頃, それから先生は小使室で悠然とお茶を飲んでおられた」(小平) とある. これに関して, 矢野は, 上掲の [矢野7] と同様の逸話を [追想高木] (pp.128-129) や [矢野2] (p.21) などでも披露している. 話としては面白いが, これが実話なのか矢野の創作なのかは判らない. 実話であるとしても, 真の理由に関しては別問題である. 貞治流のユーモア (矢野が揶揄われた) という可能性も否定できないからである. 少なくとも, この矢野が述べる内容と同一の理由が記載された (他の教え子達による) 著作を私は見かけたことがない. [追想高木] では, 矢野の他に, 浅野が唯一, この理由に関して貞治に尋ねた人物の話題を提供している (p.100). |
|||
| 講義の場合には, 10時頃すでに先生は教授室まで来ておられたのに, 何故か30分の間をおいて開始されるのであった. その理由を, 図らずも,
一年先輩の木下佳寿氏から聞く機会があった. 同氏は卒業式の日に「先生はいつも10時半から講義をされましたが, それはなぜでしょうか」と直接に高木先生に質問された由で,
そのときの答えは次のようであった. 「もともと学生諸君は10時には遅れずに教室に来ておらなければならない. そして30分の間にこの前はどんなことを学んだかを調べ, それを復習して, 続いて聴く講義に対して準備を整えておくべきである. クラインがこのようにやってみてたいへん有効であったといっている.」 |
|||
| 上記引用部において, 講義時間が規定よりも短かかったにも拘らず, その内容は豊富で充実していたという記載が, 複数箇所に見られる. 無駄がなく同じことを繰り返しさない, という記載も散見される. 彼らの卒業年度から見て, 多くの者は, 貞治が類体論の創始者として有名になった後の時代の学生達である. 貞治を畏敬するあまり, その講義に対する盲目的な崇拝もあったであろう. 例えば, 講義中の貞治の声は小さくかった, あるいは, 黒板に書かれる文字は薄かった, などの状況に関しても,「高木貞治」を畏敬する教え子達には, 何か深淵なものに思えてくるものらしい. 引き続き, [追想高木] から引用する. |
|||
| 先生が親指と人さし指でチョークを持たれ, 黒板をいたはるかの如くに字を書かれ, 声帯に負担をかけまいとするかの如くに静かな声で講演されたことを思ひ出す (佐藤良一郎 [1916], p.17) | |||
| 先生に最初に御免謁したのは大正11年 (1922) の最初の御講義の時であった. 当時の理学部本館の階段教室で, 十数名の新入生は何となく遠慮して, 皆少し後の席に坐っていた. 先生のお名前は入学前より存知あげておったので, 緊張してお待ちしておった. いざ御講義が始まり, ノートを取ろうとしたところが, お声が聞きとれない. 皆呆然としているうちに御講義は終ってしまった. 私にはこれは頭をどやされたようなショックであった. (増井真須夫 [1925], p.27) | |||
| 講義は, 我々の方に向って, 笑みを含みながら静かな口調でゆっくりと話される. 同じことは繰り返されないが, 抽象的な事柄でもまるで目前にあるもののようにありありと話されるので誠に心地よく理解することができた. 要所へくると少し声を高められる. よく白墨の先を小さく折ってから黒板へうすく式や図を描かれる. (寺阪英孝 [1928], p.42) | |||
| 私が高木先生に始めてお目にかかったのは, 東大数学科に入学を許された昭和3年 (1928) 4月で, この月に先生の「代数学」の講義とその演習に始めて出席した日のことであった.
先生の講義は明晰であることはもちろんであるが, 同じことを繰り返しては言われないことが特徴であった. (中略) ただしお声が大きくはなく, また黒板に書かれるチョークの字も稍々薄い (中略). 高木先生の講義は繰り返しをされないので, いささかの懈怠も許されず, 真の学問修行の座に列しているような喜びがあった. (吉田耕作 [1931], pp.72-73) |
|||
| 憧れの高木先生の整数論の講義はユニークだった. (中略) 奇麗な建造物か彫刻でも仰ぎ見るように雄大壮大だった. 講義の後は何回か繰り返し反すうの必要があった. (倉石治七郎 [1931], p.79) | |||
| 指先でつまむようにチョークを持って書かれる板書の文字はうすく, 悠然たる話し方ではあったが, 言葉数は少なく声は小さくて, 目をこらし耳をそばだてたものである.
ゆっくりとした調子で講義を進めておられるようにみえたが, 後になって講義のノートを調べると, 意外に内容が豊富で, (中略) 先生の講義は, (中略) 長年繰り返して推敲を重ねられたもので, 実によくまとまっている. いかに多くを盛り込むかではなく, つねに本質的なものを念頭において, 省くべきは省いて, いかに短くするかに本格的に苦心を払われたものである (中略). 定理の証明一つにもそれなりの工夫のあとが感じとられ, エレガントな証明が随所に見出される. 理論の展開は鮮かで分りやすく, 私にとっては芸術品にも似た香り高い魅力的なものであった. (浅野啓三 [1933], pp.97-98) |
|||
| 高木先生は真に数学を愛し, 理解し, 純粋に数学の中に没入し, 俗世界に左右されず, かと言って俗世間を蔑視せず, 愛想笑いをせず, 怒りの表情を微塵も出さず, 人の気持を忖度するような面倒なことは一切せず, 三十数分の授業をいつも淡々とひとりごとのように楽しんで語る. (安部道雄 [1933], p.107) | |||
| 高木先生の御講義は始まったが, ここでも困ったことがおこった. それは先生のお声がいかにも小さく, また黒板にかかれる字もいかにも小さいことであった. それでも聴き落としたりすることがあっては大変なので, 講義の後では, あちらこちらの参考書を読み, ノートの整理は大変であった. (矢野健太郎 [1934], p.129) | |||
| 声はどちらかといえば低い方で, 広い教室の後ろの方に席をとるとききとりにくいこともあった. 黒板の文字や式はやや小さめではあったがていねいにきれいに書かれた. (古屋茂 [1938], p.158) | |||
| 高木先生は声も小さく黒板に書かれる字も薄かったので, 後の方の席に坐ったわれわれにはよく聞こえないし見えなかった. (小平邦彦 [1938], p.161) | |||
| これらを読む限りでは, 貞治への畏敬の念を強くもつ学生, あるいは学力の優秀な (あるいは学力優秀だと周囲から認められたい) 学生は, 貞治の講義を肯定的に捉える傾向があるように見受けられる. 言い換えれば, 貞治の講義を理解できないこと, あるいは貞治の講義方法を肯定できないこと, その原因を全て自己の学力不足や努力不足に帰する傾向がある (従って, 自ら努力してこれを理解し, これを肯定的に捉えるように努めている) ように思われるのである. その一方, やや距離を置いてこれを客観的に捉える者も存在する. |
|||
| 高木先生は数々の名著をあらわされたが, (中略) 高木先生の書かれた本とその講義について少くとも外見的には非常に隔りがある (中略) 高木先生の御本は理路整然, 懇切叮嚀, 快刀乱麻, 時にはジョークを交えて流麗の筆になるようです. これに対し御講義の方は, 少くとも昭和初頭の頃在学した学生達にとってはかなり難渋な, 更には神韻縹渺として捕らえがたいもののようでした. なぜあのように著書と講義の間に違いがあるのだろうか. 著書は一般の人にも読まれるものだから判り易く明快に書くことが必要で, 講義は大学の数学専攻の学生達だけがきくものだから要点だけを簡単にと配慮されたとも考えられます. 要はこれを聴く学生側にあるというわけで, これをたとえようもない名講義とし, とぎれとぎれの要点から珠玉の思想を汲みとるか否かは学生の腕前という考えです. (恒川実, p.82) |
|||
| 私は, この恒川の見解に与する者である. 貞治の著書は確かに「理路整然」であり「明快」と言えよう. 一回につき僅か30分の講義で一つのトピックを纏め, 緩やかに進む通年の講義で『解析概論』の大半を終えることは, やや無理があるように思う. 要点のみの講義であったからこそ, 聴講後, 学生達は他の数学書を調べたりノートを整理しながら復習したりする必要が生じたのであろう. ここに見られる彼らの自己研鑽力は, 現代における一般の大学生のそれとは雲泥の差がある. それを貞治への憧憬に後押しされるながら苦ともせず継続し得たからこそ, 彼らもまた優秀な数学者と成り得たのであろう. |
|||
| §6-4. エッセンシャルとトリビアル | |||
| 貞治は,『微積の體系といつたようなこと』において,「微分のことは微分で…」のような考え方は, 両足が揃っているのに敢えて片足で歩行するような無益な苦行と断じた. 貞治の著書が明快で理路整然としている最大の理由として, 論理の流れおよび証明の手法が自然であることが挙げられよう.『初等整数論講義』や『解析概論』における独自の工夫を加えた説明あるいは証明は, 読者を感嘆させるものが多い.『高等敎育代數學』に掲載された問題に対する解答は, その手法に関して何れも鮮やかで美しく, やはり読者を感嘆させる. そこでは, 問題に解答する際は単に正答を得ればよいわけではない, 常に単純明快を旨とせよ, と学生達に注意を与えたのであった. また, 貞治は, 自身を等身大以上に見せたり過大評価されたりすることを好まず, 数学に対しては厳密な理解を旨とし, 理解不足を決して誤魔化さない謙虚さを兼ね備えていた. このような貞治の学究姿勢ないし教育方針は, 折に触れて教え子達にも伝授されたようである. [追想高木] には次のような回想が記されている. |
|||
| ゼミにおいて, 菅原さんはヘッケの数論の教科書 (1923), 正田さんはフロベニウスとシューアの論文を (中略) 講読され, 問谷さんはシュパイザーの群論の初版 (1922) を講読に用いられた. このゼミは三人の熱意が直かに感ぜられるようなゼミであった. 高木先生は, 温顔を以て静かに講読を聞かれておられたが, 時々「そうは行かぬ」と仰せられた. そうすると講読者はほとんどかならず立往生をされてしまった. まことに鋭い御指摘であった. (増井真須夫 [1925], p.28) | |||
| 私達が初期の頃, 何かといえば鉛筆を取って計算などを始めようとする態度をたしなめられた (中略) 書物は "lessen zwischen den Zailen" (行間を読み取れ, 眼光紙背に徹する) とか言われた (寺阪英孝 [1928], p.44) |
|||
| 寺阪は, 貞治の言葉として「書物は行間を読み取れ」と記しているが, 寺阪以外の者がこれに関して言及しているのを私は見掛けたことがない. 寺阪は, 上記引用部以外にも, |
|||
| [寺阪]『幾何学研究の思い出』/ 寺阪英孝, 南雲道夫, 守屋美賀雄 共著『数学のながれ』上智大学数学教室, 1977, p.6. | |||
| において,「高木先生の本を読む態度としての教訓は, Lesen zwischen den Zerilen (行間を読め) ということであった.」と記している. 但し, これに関して, 貞治自身が『解析概論』の「緒言」に同様の文言を記していることは既に述べた通りである (§4-9.). |
|||
| ゼミの第一回目, よくわからない本の内容と悪戦苦闘やっと話し終えた途端, 先生がおっしゃった「ちっとも面白くない」, これにはぎゃふん. 結局要点だけを簡明に言えばよかったのに, 始めから終わりまでだらだらと冗長に話したのがお気に入らなかった次第. あらかじめ一言, 要点だけを簡単に話せばよいのだよと注意されないところが, 先生の面目躍如たるところでしょう. 数学科の学生たる者は, 注意されなくとも自得すべきだという, 一生忘れ得ない御教訓だったようです. (恒川実 [1931], p.83) |
|||
| 演習の時間は特にこわい時間であるとともに数学を考究する態度を悟らせるものであった. へまなことをしていると横を向いていた先生が「そんなことそしていてはしようがない」やがて「退れ」と言われる. (小松醇郎 [1932], p.87) | |||
| 当時は, 数学抽象化の盛んな時代であった. 高木先生は, よく「看板の塗り替え」などと皮肉を言われたが,「看板も塗り替えている中に, 何かが出て来るかもしれない」と言われもした.
(中略) セミナーではたった一回だけ, イデアル論の中で使われていた選択公理の役割が面白くて, ここは熱を入れて報告した. 先生は何か, にやにやされながらそれを聞いておられたが, 最後に一言,「ペダンティックだね」と言われた. 著者に対してか, 報告者に対してか, とにかく私には, この一言は身に沁みてこたえた. (小野勝次 [1933], pp.93-94) |
|||
| 先生のよく口にされた言葉で, エッセンシャルとトリヴィアルがいつまでも私の耳に残っている. 先生流にいえば,「数学で何かがよく分ったというのは, 何から何まで, すみからすみまでよく分ったということではなく, 何がエッセンシャルで何がトリヴィアルであるか, その区別がよく分ったということである. エッセンシャルなものを追求し, 重視する, 重要性の認識が本質である.」(浅野啓三 [1933], p.98) | |||
| 先生は (中略)「君, ラゲールの全集を読んでみないか」と言われた. 先生のお考えはすぐに分かった. ラゲールの論文は方法が奔放であり着想が面白いということを一年生のとき講義か演習で聞かされていた.
ラゲールは解析を用いて代数の定理を得ているが, これらは純粋に代数的な方法で証明し直せるはずであるから, やってみよというのが先生のお考えであると思った.
(中略) うまくいったのはスツルムの問題に関するいわゆるラゲールの定理だけであった. しかしその代数的証明を求めるということは先生が絶えず気にしておられたものらしく,
私の証明を聞いて下さったとき, 一言「よくやった!」と仰言って下さった. 嬉しかった. なお, その証明をあとで先生の『代数学講義』の改訂版に載せて下さった.
(中略) ある時, (中略) シュタイニッツの定理は証明が面倒であるが如何でしょうかと伺ったところ,「ああいうものは, あるものとして……」とさりげなく仰言った. 軽くいなされたわけである. と同時に私はハッとした, この類の定理は, (中略) その概念の認識に立ってその先を考えるところに意味がある, というのが先生のお考えのように思われて, 私は目を開かれる思いがしたのであった. (中略) 一年生のときの代数学演習の時間に, 誰かが「帰納法で証明します」とやったところ, 終ったあとで「帰納法は素人のやるものだ」と仰言った, これも妙に心に残っている. (村勢一郎 [1937], p.117, p.119) |
|||
| 演習のとき, この証明はよくないなどと余計なことをつい口にしたら, 先生から数学の証明にはよしあしの判定基準はないとたしなめられた. 先生のお言葉ながら果たしてそうだろうか.
そこで, 自分が当たったとき, 整数論の演習問題を解くのに, 微積分をつかった証明を板書して引き下がった. 先生は嫌な顔をなさっている. しかし先日のことがあるからお叱りになるわけにも参らぬとお見受けした.
(中略) 高木先生はよく言われた.「何が essential で, 何が trivial か, その区別が大切である.」「いかに怠けるかが大切である.」「自分で機関車にならなければ数学者になれない.」(北川敏男 [1934], p.121, p.125) |
|||
| 私達が, 先生の方法と異った解法を外国書などで見出して先生にお話申上げると「そんな方法でやるとコーシー先生が泣くよ」などと言って笑っておられた
(中略) 「学究の徒は, なにがエッセンシャルであり, なにがトリヴィアルであるか, を見極めることが肝腎である」といわれたことがあった . (山内正憲 [1935], pp.136-137) |
|||
| 先生はしばしば独特のうまい言いかたで数学の感覚的内容を示唆なさった. (中略) 三角級数のところでファイエ (Fejér) (中略) の定理の証明にうまい計算を示され,「こんなズルイ計算なんかして……」と言われたのである. 賞めっぱなしにはしたくないお気持ちが窺われた. (中略) 大は小を兼ねるという辞書式網羅主義を, 先生は採られなかったように思う. たとえば有限項のテイラー展開で最後の剰余の項はいろいろに表わすことができるのであるが, 私たちは最も標準的なものを一つ知ればよかった. 時間がもっとあればやるというのではなく, あったとしても敢てそれはやらないのである. (中略) 不定形の極限といわれたものについても, 実解析的定理については触れられていない. テイラー展開を知っていれば済むことだからである. (中略) 正項級数の収束・発散の判定条件ではガウスの条件を代表に選ばれた. (中略) 先生の御講義の中でも複素関数の部分は圧巻であった. われわれはほとんど陶酔したといってよい. 私自身も先生の魅了する力の虜になったために解析学の一分野にのめり込んだらしい. (亀谷俊司 [1936], pp.141-142) |
|||
| 講義は, 実数の性質として, 上に有界な単調増加列は極限値をもつということを前提として始められました. 厳密にいうといくらでも遡ることになるから, この辺から始めるとおっしゃった様に記憶しています. 私は『新撰算術講義』で実数の厳密な定義をしておられるのを覚えてましたので, この出発のしかたは意外でしたが, 暫らく聞いている中に先生が直観と論理とのバランスを考えて講義を進められるのがよくわかりました. (伊藤清 [1938], pp.165-166) | |||
| 先生の示されたお考えの一端, 例えば「若い者は三つのAとGという分類によって専門化されず, 広くモダンな数学を勉強しなければならない」とか「essential と trivial の区別が肝要である」と言うようなことは, われわれ学生仲間の間の標語となっていた. (河田敬義 [1938], p.168) | |||
| 先生が黒板に書かれる字は, うすいけれど丁寧に書かれました. (中略) ゼミナールの時, 話がつまらないと窓の方を向いたりしていました. つまらないことを長くは御免だという気があるんでしょう. (三村征雄 [1928], pp.205-206) |
|||
| 貞治は, 自身がその講義や著書で見せた「独自の工夫を加えたエレガントな手法」を, ゼミにおいて学生達にも (口にしないまでも) 求めていたのであろう. 意に沿わない発表をする学生達には,「面白くない」あるいは「退れ」と言ったり「横」あるいは「窓の方」を向いたりしつつ, それを伝えたのであった. 「エッセンシャル」と「トリヴィアル」に関しても多くの教え子達を感化したようである. これは, 前出の西田幾多郎にも見られる学究姿勢であった.「本物の哲学者には必ず独自な考え方がある. 書物を読むというのは, その骨をつかむことだ.」あるいは「骨がわかってしまえば, 何も最後のページまで読む必要はない」というものである (高山岩男『西田哲学とは何か』燈影舎, 1988). |
|||
| §6-5. 貞治のプロフィール | |||
| 『高數硏究』第1卷第1號 (1936年10月) pp.55-56 には,「數學者のプロフヰル 高木貞治博士」が掲載されている. 執筆者は「X・Y・Z」を名乗る匿名の人物であるが, 貞治に近い位置にいた者 (あるいは貞治に直接取材できた者) であることがその内容から窺える. 少し抜粋してみよう. |
|||
| 1932年秋瑞西のチユーリツヒで萬國數學大會が開かれた折の事である. この榮ある大會の議長は誰あらうわが高木博士その人であつたのだ. (中略)
博士は一夕出席の人々を招待された事があつた. 定刻に先だつて若々しい一人の學者がやつて來て博士に會釋したと思ひ給え. ニ三の會話が交はされた後で博士は型の如く「あなたはどちらです?」ときいたものだ.「僕ライプチヒです.」「では,
フアン, デア, ヴェルデン氏は御存知なわけですねえ.」「え, え, よく知つてゐます. 私自身のことですもの.」「えつ, あなたが……いやこれは」 あの謹嚴な顔の相好を崩して頭に手をやつたその折の博士を想像することは何と朗らかな光景ではないか. 博士とヴェルデンとは相識の間柄であつたにも拘らず博士にこの失敗があつたのは世界的代數學者ヴェルデン氏が余りに若々しかつたからで, 必ずしも博士の記憶力が鈍かつたからではない. |
|||
| ファン・デル・ヴェルデンの5巻書 |
|||
| [Waerden1] ファン・デル・ヴェルデン (銀林浩訳)『現代代数学 1,2,3,I,II』東京図書, 1959-1960, 1967-1971. | |||
| は, 私にとっては (学生時代を想い出させる) 懐かしい数学書である. 演習書2書も解説が懇切丁寧であり, 初学者には読み易いものであった.
チューリッヒにおける国際会議が開催された1932年時点での彼は僅か29歳であったが, 代数学の抽象的構造を説いた |
|||
| [Waerden2] "Moderne Algebra", Unter Benutzung von Vorlesungen von E. Artin und E. Noether." Teil I,II, Springer, 1930-1931. | |||
| をもって既に有名な存在であった. 「數學者のプロフヰル 高木貞治博士」には, 続けて |
|||
| それどころか, 博士の記憶力と來たら, まさに我學界のレコードである. 博士は大學の學生時代かつてノートを取つたことがなかつたと云ふ程だ.
どの講義も聞き流しであつたが何時でも成績はトツプ, 同級であつた吉江博士曰く,「體操と製圖だけは僕の方がうまかつたがね.」(中略) 講義ぶりが亦博士獨特のもので, 聞きとり難い低聲, 然も肝腎なところになると一人でニコニコしながら一層小聲になる. おまけに白堊の尖端をつまんで輕く書かれる板書の文字が薄いと來てるので, 大抵の學生は惱まされる. (中略) 敎室に顔を見せられるのは大抵30分もすぎた頃で, 敎壇に経つて白堊をつまむ. それがお辭儀だ. (中略) 三高時代本科一年から吉江博士とずつと同級, 大學の同級生は入學當初8人であつたが, 卒業の時は吉江博士とたつた2人. もつとも一年先輩であつた故林鶴一博士が病氣のため同級になられたので3人になつた. |
|||
| と記されている. 当時の数学科は卒業することなく退学もしくは他学科へ転科することも少なくなかったらしい. 前出 (§6-1.) の八田三喜も貞治や吉江と同期であるが, 数学を断念して後に哲学科に再入学している. §5-3. に挙げた「高木・吉江兩博士を圍む會」(『高數研究』第3卷第7號, 考へ方研究社, 1939, pp.36-45) において,「8人這入つたのですが, それが卒業の自分は, 高木君と自分と2人しか居ないのです.」と吉江が述べ,「林鶴一先生は上でしたか」という藤森 (良夫) の問いに, 吉江は「あれは, 僕等より一年上でしたが, 病氣で一年遅れられたので, 卒業年度は同じでした.」と述べている. 中学および高校時代に貞治が丁寧なノートを作成していたことは, §1.において既に見た通りである. 大学時代にノートを全く作成していないというのは, 俄かには信じがたい. [百年史上] p.164 の脚注には,「(吉江は) 克明に筆記したノートを残した. そのノートは現在東大数学科図書室に保存されている.」とある. 他に何も記載がないところを見ると, 貞治のノートは東大には保存されていないのであろう. |
|||
| 小石川曙町學者街の一角, 古色蒼然たる住居には, 大きな熊の皮と古びたピアノとがある. いかにも學者らしい素朴な室で, 博士は一日二度の睡眠をとる. 夕刻二本の晩酌に陶然となつてぐつすり一寝入りし12時頃に書斎に現はれ, 東の白む頃まで讀書三昧, それから再び寝室に歸るといつたやり方である. | |||
| 晩酌および夜半からの研究に関しては上掲した (正田建次郎の記述). さらに, [追想高木] における小松醇郎 (1909-1993) の回想を見ると, |
|||
| 高木・掛谷両先生の酒豪は有名で, 岩波茂雄氏が「Mathematiker muss tinken, Philosopher muss reuchen.」と言ったものである. 西田幾太郎さんはよほど煙草を吸ったものとみえる. 煙草といえば戦前, 戦中に, 二度高木先生のお宅をお尋ねしたことがある. (中略) 一時間と少しくらいで見る間に灰皿に吸い殻が山とつまれたことを憶えている. | |||
| とある. これによれば, 貞治は相当量の酒と煙草を摂取したように見える. なお,「西田幾太郎さんは……」(正しくは幾多郎) とあるのは, まだ煙草と縁のなかった若い頃の幾多郎が恩師ケーベル (Raphael von Koeber, 1848-1923) から "Philosopher muss reuchen" (哲学者は煙草を吸わざるべからず) と揶揄われたという逸話 (『西田幾多郎全集 第 第12巻』p.243,『西田幾多郎全集 第13巻』p.177, 岩波書店, 1989) に基くのであろう. 「數學者のプロフヰル 高木貞治博士」では, さらに続けられる. |
|||
| 博士はあれで中々のお洒落で, いつもリユウとした風采, あの福々した太い耳に靑年らしい若々しさを漂はし, 氣分が向けばいくらでも駄べつて飽くことを知らない. (中略) 一度話題がほころびると映畫ござれ, 演劇ござれ, 世界の名のある作品は大抵讀んでゐるといふ深い趣味に, 忽ち參つて了ふものだ. | |||
| [本田] によれば, 貞治はドイツ留学時代, 演劇を好み, 観劇に出かけたという (§2-4.). [追想高木] においては, 貞治の三男佐知夫は |
|||
| 父は芝居が好きであった. 大阪へ行ったときは, 文楽も見てきた. 晩年は映画も見に行っていた. ユリアス・シーザーとか, 戦争と平和など. | |||
| と述べている (p.210). また, 文学も好んだらしく, | |||
| 外国文学も好きで, 19世紀のドイツ物, 例えばハウプトマンの物など好んで読んでいた. | |||
| とある (p.210). また, 宇野利雄 (1902-1998) は, |
|||
| あるとき何かの用事で先生のお室に伺った. たまたま机上に眼をうつすと, メーテルリンクの la Sagesse et la Destinée がそこに置かれてあった. この本について語られることは, 私は伺う機会がなかったが, 机上にこれが置かれてあったときの感動はいまだに私の心をつらぬいている. | |||
| と述べている ([追想高木] p.39). 彌永昌吉は, [彌永8] p.19 において |
|||
| 戦争の末期 (お宅の焼けたあと), 東大数学教室の疎開していた諏訪まで, 先生が来られたことがあった. 旅館で,「何か読むものはないのか」といわれた. 私はちょうどレクラム版のチェーホフ短編集をポケットに入れていたので,「これでも如何でしょうか」と申しあげたところ, 大変喜ばれ, 細かいドイツ字100ページばかりのその本を, 一晩で読んでしまわれた. ―― もう70に近いお年の時のことである. | |||
| と記している. 仏語で文学者の評論を読んだり, 独語でロシア文学を読んだり, | |||